Cím:	Az 1983. évi (14.) Nemzetközi Fizikai Diákolimpia feladatai
Füzet:	1983/november, 161 - 167. oldal	PDF  |  MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A XIV. Nemzetközi Fizikai Diákolimpia feladatai   Elméleti feladatok   1. Egy részecske egydimenziós mozgást végez az $OX$ pozitív féltengely mentén. A részecskére ható $F\left(x\right)$ erőt az 1. ábra mutatja. Az $O$ origóban egy tökéletesen visszaverő fal van. Ugyanakkor a részecskére mindenhol hat egy súrlódási erő is, amelynek nagysága $F_f=1\mathrm{,}00\text{<span style="font-style: italic;"> N</span>}$. A részecske az $x=x_0$ pontból indul $E_0=10\mathrm{,}0\text{<span style="font-style: italic;"> J</span>}$ kinetikus energiával. 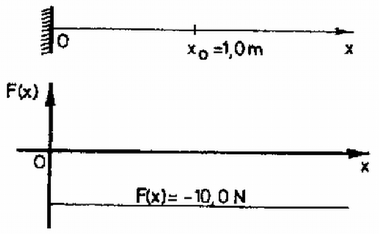  1. ábra   a) Határozzuk meg, milyen hosszú utat tesz meg a részecske a végleges megállásig! b) Ábrázoljuk grafikusan a részecske $U\left(x\right)$ helyzeti energiáját az $F\left(x\right)$ erőtérben! c) Ábrázoljuk kvalitatívan a részecske sebességét az $x$ koordináta függvényében!   Megoldás. $a)$ A grafikonról leolvashatjuk, hogy a számunkra érdekes $x>0$ tartományban az $F\left(x\right)$ erő nem függ $x$-től, tehát egy $F=10$ N nagyságú, balra ható erőről van szó. $x>0$ esetén a részecskére ható súrlódási erő kisebb, mint az $F$ erő, ezért a részecske csak az origóban állhat meg véglegesen. A visszaverő falon addig fog pattogni, amíg a helyzeti és mozgási energiája teljes egészében a súrlódási erő ellen végzett munkává alakul, azaz $F_{f}s=x_{0}F+E_0$, ahol $s$ a megállásig megtett út, $x_{0}F$ pedig a helyzeti energia megváltozása az indulás és a megállás között. Az egyenletből $s$-et kifejezve és az adatokat behelyettesítve $s=20$ m-t kapunk.   $b)$ Állandó erő által létrehozott erőtérben a helyzeti energia $E_P=F_x+c$, ahol $c$ tetszőleges állandó. $c$-t nullának választva, a keresett grafikon a 2. ábrán látható. 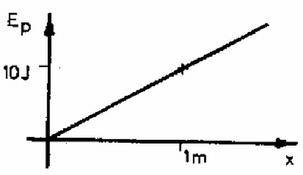  2. ábra   $c)$ Ha a részecske balra mozog, akkor a gyorsulása $a=-\left(F-F_f\right)/m$. Ha $x\text{'}$-vel jelöljük azt a helyet, ahonnét balra indul, akkor a helyére és sebességére a következő egyenleteket írhatjuk fel: $\begin{array}{c}{\displaystyle x=\left(a/2\right)t^2+x\text{'};v=at\mathrm{.}}\end{array}$ A három egyenletből $\begin{array}{c}{\displaystyle v=-\sqrt[]{\left(x-x\text{'}\right)2\frac{F_f-F}{m}}\mathrm{.}}\end{array}$ (1) Ha a részecske jobbra mozog, akkor $a=-\left(F+F_f\right)/m$. $v\text{'}$-vel jelölve azt a sebességet, amellyel a falról visszapattan, helyének és sebességének egyenlete most $x=\left(a/2\right)t^2+v\text{'}t$; $v=at+v\text{'}$, innen $\begin{array}{c}{\displaystyle v=\sqrt[]{{\left(v\text{'}\right)}^2-2\frac{F+F_f}{m}x}\mathrm{.}}\end{array}$ (2) Az (1) és (2) függvények a $\sqrt[]{x}$ függvény transzformáltjai, tehát paraboladarabok. Attól függően, hogy a testet az $x_0$ pontból balra vagy jobbra indítjuk, kétféle mozgás lehetséges. A két esetben a keresett $v\left(x\right)$ grafikont a 3. ábrán ábrázoltuk kvalitatívan.  (8 pont) 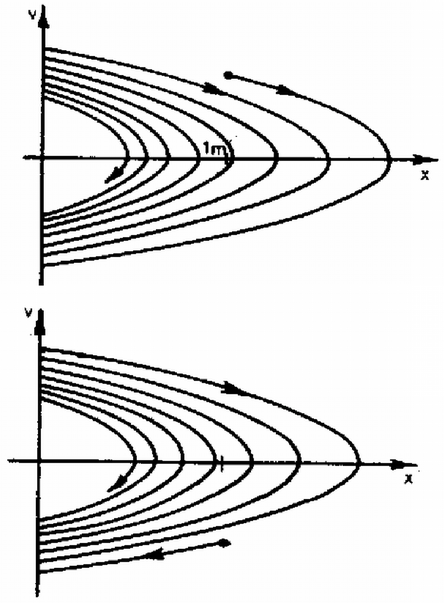  3. ábra     2. A $4$. ábra szerinti áramkörben $L_1=10\text{<span style="font-style: italic;"> mH</span>}$, $L_2=20\text{<span style="font-style: italic;"> mH</span>}$, $C_1=10\text{<span style="font-style: italic;"> nF</span>}$, $C_2=5\text{<span style="font-style: italic;"> nF</span>}$ és $R=100\text{<span style="font-style: italic;"> k</span>}\Omega$. A $K$ kapcsoló hosszabb ideje zárva van. Az áramforrás $f$ változtatható frekvenciájú szinuszos áramot ad, de az áramforrás áramerősségének amplitúdója állandó. a) Jelöljük $f_m$-mel a maximális hatásos teljesítményhez ($P_m$-hez) tartozó frekvenciát és $f_{+}$-szal, ill. $f_{-}$-szal az $\left(1/2\right)P_m$-hez tartozó frekvenciákat! Határozzuk meg $f_m$, és $\Delta f=f_{+}-f_{-}$ arányát! A $K$ kapcsolót kinyitjuk. A kapcsoló nyitása után egy $t_0$ pillanatban az $L_1$ és $L_2$-n átfolyó áramerősségek $i_{01}=0\mathrm{,}1\text{<span style="font-style: italic;"> A</span>}$, $i_{02}=0\mathrm{,}2\text{<span style="font-style: italic;"> A</span>}$ és a feszültség $U_0=40\text{<span style="font-style: italic;"> V</span>}$. b) Számítsuk ki az áramkör $L_1{C}_1{C}_2{L}_2$ része sajátrezgésének a frekvenciáját! c) Határozzuk meg az $AB$ vezetőben az áramerősséget! d) Számítsuk ki az $L_1$ tekercsben az áramerősség rezgésének amplitúdóját! 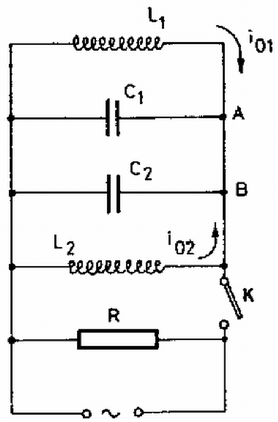  4. ábra   Megoldás. $a)$ Jelöljük $Z$-vel az áramkör eredő impedanciáját! A párhuzamos kapcsolás miatt $\frac{1}{Z^2}=\frac{1}{R^2}+{\left(C\omega -\frac{1}{L\omega }\right)}^2$, ahol $C=C_1+C_2$ és $L=\frac{L_1{L}_2}{L_1+L_2}$ az eredő kapacitás és induktivitás. A hatásos teljesítmény: $\begin{array}{c}{\displaystyle P=\frac{U^2}{R}=\frac{I^2{Z}^2}{R}=\frac{I^2}{R}\frac{1}{\frac{1}{R^2}+{\left(C\omega -\frac{1}{L\omega }\right)}^2}\mathrm{.}}\end{array}$ (1) Ebből látható, hogy $P$ akkor maximális, ha $C\omega -\frac{1}{L\omega }=0$, azaz a rezgőkör rezonanciában van. Így $f_m=\frac{1}{2\pi \sqrt[]{LC}}$. Szintén az (1) összefüggésből olvashatjuk le, hogy a teljesítmény akkor lesz a maximális fele, ha $\frac{1}{R^2}={\left(C\omega -\frac{1}{L\omega }\right)}^2$, azaz $\begin{array}{c}{\displaystyle \frac{1}{R}=C{\omega }_{+}-\frac{1}{L{\omega }_{+}}\text{és}-\frac{1}{R}=C{\omega }_{-}\frac{1}{L{\omega }_{-}}\mathrm{.}}\end{array}$ Átalakítva: $\begin{array}{c}{\displaystyle {\omega }_{+}-{\omega }_{-}=\frac{1}{RC}\mathrm{,}\text{így}\Delta f=\frac{1}{2\pi RC}\mathrm{.}}\end{array}$ Az eredmény $\begin{array}{c}{\displaystyle \frac{f_m}{\Delta f}=R\sqrt[]{\frac{C}{L}}=150.}\end{array}$ $b)$ A megadott adatokkal $L_1{C}_1=L_2{C}_2$, tehát az $L_1{C}_1$ és az $L_2{C}_2$ rezgőkör ugyanazzal a frekvenciával oszcillál egymástól függetlenül. A sajátrezgés frekvenciája tehát $\begin{array}{c}{\displaystyle f=\frac{1}{2\pi \sqrt[]{LC}}=\frac{1}{2\pi \sqrt[]{L_1{C}_1}}=15\mathrm{,}9\text{ kHz}\mathrm{.}}\end{array}$ $c)$ A két rezgőkör függetlensége miatt az $AB$ ágban nem folyik szinuszos áram. A tekercsek ellenállása egyenárammal szemben zérus, ezért egyenáram folyhat az $AB$ ágban. Jelöljük $i_{c_1}$ és $i_{c_2}$-vel a $t_0$ időpillanatban a $C_1$ kondenzátorból $A$-ba, ill. a $C_2$-ből $B$-be folyó áramerősséget! ${\displaystyle \begin{array}{c}\hfill {\displaystyle i_{c_1}=C_1\frac{\Delta U}{\Delta t}\text{és}{i}_{c_2}=C_2\frac{\Delta U}{\Delta t}\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{így}{i}_{c_1}=\frac{C_1}{C_2}{i}_{c_2}\mathrm{,}\text{azaz}{i}_{c_1}=2i_{c_2}\mathrm{.}}\hfill \end{array}}$ Az $A$ és $B$ pontokra a csomóponti törvény: $\begin{array}{c}{\displaystyle i_{AB}=i_{01}+i_{C_1};i_{AB}=-i_{02}-i_{C_2}\mathrm{.}}\end{array}$ Az utóbbi három egyenletből $\begin{array}{c}{\displaystyle i_{AB}=\frac{i_{01}-2i_{02}}{3}=-0\mathrm{,}1\text{ A}\mathrm{.}}\end{array}$ $d)$ Jelöljük $r$ indexszel azt az áramerősséget, amit a rezgőkör rezgése hoz létre! $i_{01r}=i_{01}-i_{AB}=0\mathrm{,}2\text{ A}$.   Az $L_1{C}_1$ rezgőkörben az energiamegmaradás szerint $\begin{array}{c}{\displaystyle L_1\frac{i_{1r\text{max}}^2}{2}=L_1\frac{i_{01r}^2}{2}+C_1\frac{U_0^2}{2}\mathrm{.}}\end{array}$ A keresett áramerősséget kifejezve: $\begin{array}{c}{\displaystyle i_{1r\text{max}}=\sqrt[]{i_{01r}^2+\frac{C_1}{L_1}{U}_0^2}=0\mathrm{,}204\text{ A}\mathrm{.}}\end{array}$  (8 pont)   3. Két prizmát, amelyek törőszőge ${\widehat{A}}_1={60}^{\circ }$, ${\widehat{A}}_2={30}^{\circ }$, az $5$. ábrának megfelelő módon összeragasztottunk $\left(\widehat{C}={90}^{\circ }\right)$. A törésmutatókat a következő képletek adják meg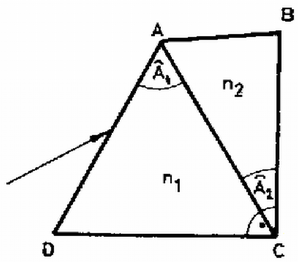: $n_1=a_1+b_1/{\lambda }^2$; $n_2=a_2+b_2/{\lambda }^2$, ahol $a_1=1\mathrm{,}1$; $b_1={10}^5{\text{ nm}}^2$; $a_2=1\mathrm{,}3$; $b_2=5\cdot {10}^4{\text{ nm}}^2$.   5. ábra   a) Határozzuk meg azt a ${\lambda }_0$ hullámhosszat, amelyre bármely irányból érkező fénysugár törés nélkül halad át az $AC$ felületen! Határozzuk meg az ehhez az esethez tartozó $n_1$ és $n_2$ törésmutatókat is!   b) Rajzoljuk meg, hogy hogyan halad át a prizmarendszeren az ábra szerint beérkező, három különböző fénysugár, amelyek hullámhossza ${\lambda }_{\text{vörös}}$, ${\lambda }_0$, és ${\lambda }_{\text{kék}}$! Legyen a fénysugarak beesési szöge azonos!   c) Határozzuk meg, hogy a ${\lambda }_0$ hullámhosszú sugárzásra mekkora a prizmarendszer legkisebb eltérítési szöge!   d) Határozzuk meg, hogy milyen hullámhosszú sugárzás esetén lehetséges, hogy a $DC$ alappal párhuzamosan belépő fénysugár $DC$-vel párhuzamos marad a prizmarendszer elhagyása után is!   Megoldás. $a)$ Az $AC$ felületre különböző irányból érkező ${\lambda }_0$ hullámhosszú fénysugarak akkor nem törnek meg, ha $n_1=n_2$, azaz $a_1+b_1/{\lambda }_0^2=a_2+b_2/{\lambda }_0^2$. Átrendezve ${\lambda }_0=\sqrt[]{\frac{b_2-b_1}{a_1-a_2}}=500\text{ nm}$. Ekkor $n_1=n_2=1\mathrm{,}5$. $b)$ A ${\lambda }_0$-nál nagyobb hullámhosszú vörös fényre $n_1$ és $n_2$ is kisebb, mint $1\mathrm{,}5$, míg a ${\lambda }_0$-nál kisebb hullámhosszú kék fényre mindkét törésmutató nagyobb. Nézzük még meg, hogy az $AC$ felületen hogyan változik a törésmutató. Tudjuk, hogy a ${\lambda }_0$ hullámhosszúságú fényre $n_2/n_1=1$. Ha a ${\lambda }_0$ helyett ${\lambda }_{\text{vörös}}$ hullámhosszú fényt veszünk, akkor $b_1>b_2$ miatt $n_1$ jobban csökken, mint $n_2$, ezért $n_2/n_1>1$. Hasonlóan látható, hogy kék fényre $n_2/n_1<1$. A fentiek alapján már megrajzolhatjuk a fénysugarak áthaladását a prizmán (6. ábra). 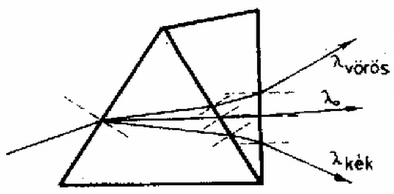  6. ábra   c) A ${\lambda }_0$ hullámhosszú fényre a prizmarendszer úgy viselkedik, mint egy ${30}^{\circ }$-os törőszögű $n=1\mathrm{,}5$ törésmutatójú anyagból készült prizma. Tudjuk, hogy egy prizmán áthaladó fénysugár akkor térül el legkevésbé, ha a prizmán szimmetrikusan halad át, azaz a 7. ábrán $\alpha$-val jelölt szögek egyenlők. 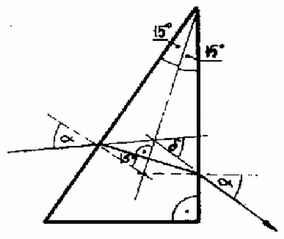  7. ábra   Ekkor a törési törvény $\frac{\text{sin}\alpha }{\text{sin}{15}^{\circ }}=1\mathrm{,}5$, innen $\alpha ={22}^{\circ }50\text{'}$.   A keresett eltérítési szög: 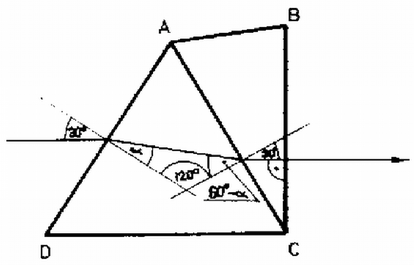$\delta =2\alpha -{30}^{\circ }={15}^{\circ }40\text{'}$.   8. ábra   $d)$ A 8. ábra alapján a következő összefüggéseket írhatjuk fel: $\begin{array}{c}{\displaystyle \frac{\text{sin}{30}^{\circ }}{\text{sin}\alpha }=n\mathrm{,}\frac{\text{sin}\left({60}^{\circ }-\alpha \right)}{\text{sin}{30}^{\circ }}=\frac{n_2}{n_1}\mathrm{.}}\end{array}$ A két egyenletből $\alpha$-t kiküszöbölve: $3n_1^2=n_2^2+n_2+1$. Az $n_1$ re és $n_2$-re adott összeíüggéseket leírva és átrendezve: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \left(3a_1^2-a_2^2-a_2-1\right){\lambda }^4+\left(6a_1{b}_1-b_2-2a_2{b}_2\right){\lambda }^2+}\hfill \\ \hfill {\displaystyle +3b_1^2-b_2^2=0.}\hfill \end{array}}$ Ez ${\lambda }^2$-re másodfokú egyenlet, aminek megoldása $\lambda =1\mathrm{,}18\mu \text{m}$. (7 pont)   4. Egy ${\lambda }_i$ hullámhosszúságú foton egy mozgó szabad elektronnal ütközik. Az ütközés következtében az elektron megáll, és egy ${\lambda }_0$ hullámhosszúságú, az előbbi haladási irányához képest $\Theta ={60}^{\circ }$-os szöggel eltérült foton halad tovább. Ezután a foton egy nyugalomban levő szabad elektronnal ütközik és egy ${\lambda }_f=1\mathrm{,}25-{10}^{-10}\text{ m}$ hullámhosszúságú fotonként halad tovább, mozgásiránya a második ütközés során is $\Theta ={60}^{\circ }$-kal változik meg. Számítsuk ki az első elektron de Broglie hullámhosszát az ütközés előtt! (Planck állandó: $h=6\mathrm{,}6\cdot {10}^{-34}\text{<span style="font-style: italic;"> Js</span>}$, elektrontömeg: $m=9\mathrm{,}1\cdot {10}^{-31}\text{<span style="font-style: italic;"> kg</span>}$, fénysebesség: $c=3\mathrm{,}0\cdot {10}^8\text{<span style="font-style: italic;"> m/s</span>}$.)   Megoldás. Az első ütközésre az energiamegmaradás: 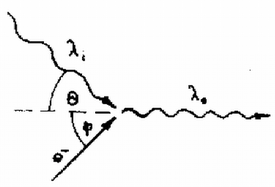$\begin{array}{c}{\displaystyle h{\nu }_0=h{\nu }_i+E_e\mathrm{,}}\end{array}$ (1) ahol $\nu$ a foton frekvenciája, és $E_e$ az elektron energiája. Az impulzusmegmaradást a kirepülő ${\lambda }_0$ hullámhosszúságú foton mozgásirányában és arra merőlegesen írjuk fel (9. ábra):   9. ábra   ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle \frac{h}{{\lambda }_0}=\frac{h}{{\lambda }_i}\text{cos}\Theta +P_e\text{cos}\phi \mathrm{,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle 0=\frac{h}{{\lambda }_i}\text{sin}\Theta -P_e\text{sin}\phi \mathrm{,}}\hfill \end{array}}$ ahol $P_e$ az elektron impulzusa. Az utóbbi két egyenletből $\phi$-t kiküszöbölve, és $\lambda$ helyére $c/\nu$-t írva $\begin{array}{c}{\displaystyle {\left(h{\nu }_0\right)}^2+{\left(h{\nu }_i\right)}^2-2h^2{\nu }_0{\nu }_i\text{cos}\Theta =P_e^2{c}^2\mathrm{.}}\end{array}$ (2) Felhasználva a $\begin{array}{c}{\displaystyle c^2{P}_e^2=E_e\left(E_e+2m_e{c}^2\right)}\end{array}$ (3) relativisztikus összefüggést, az (1) és (2) egyenletekből: $\begin{array}{c}{\displaystyle {\nu }_0=-\frac{v_i}{\frac{h{\nu }_i}{m_e{c}^2}\left(1-\text{cos}\Theta \right)-1}\mathrm{.}}\end{array}$ (4) Átalakítva: $\begin{array}{c}{\displaystyle {\lambda }_0-{\lambda }_i=-\frac{h}{m_{e}c}\left(1-\text{cos}\Theta \right)\mathrm{.}}\end{array}$ (5) A második ütközésre teljesen hasonlóan végezhetjük a számításokat, eredményül a $\begin{array}{c}{\displaystyle {\lambda }_0-{\lambda }_f=-\frac{h}{m_{e}c}\left(1-\text{cos}\Theta \right)\mathrm{.}}\end{array}$ (6) összefüggést kapjuk. Az (5) és (6) egyenleteket egymásból kivonva ${\lambda }_i={\lambda }_f$-et kapunk. A két ütközés tehát teljesen hasonló. (5) alapján ${\lambda }_0=1\mathrm{,}238\cdot {10}^{-10}\text{ m}$. Az elektron energiáját (1) alapján számíthatjuk ki: $$\begin{gathered} E_e=hc\left(\frac{1}{{\lambda }_0}-\frac{1}{{\lambda }_i}\right)= \\ =1\mathrm{,}56\cdot {10}^{-17}\text{ J} \end{gathered}$$. A (3) összefüggés felhasználásával $P_e=28\mathrm{,}4\cdot {10}^{-48}\text{ kg m/s}$. A keresett elektronhullámhossz ${\lambda }_e=h/P_e=1\mathrm{,}24\cdot {10}^{-10}\text{ m}$.  (7 pont)   A következő feladattal nem lehetett pontot szerezni a versenyben, helyes megoldásáért különdíjat adtak.   Magyarázzuk meg kvalitatívan, hogy az Olimpia emblémáján látható vízszintes tengelyű hengerre öntött folyadéksugár miért nem hagyja el a hengert a szaggatott vonal irányában, miért folyik a folytonos vonallal jelölt görbe mentén! Ez a tény az úgynevezett Coanda‐hatással van kapcsolatban, amelyet 1936-ban Henry Coanda román mérnök szabadalmaztatott. (Az Olimpia emblémáját ld. a szeptemberi számban!)   Kísérleti feladat   Rendelkezésre áll egy áramforrás (amely egy telepből és a ráragasztott ellenállásból áll), két feszültségmérő műszer (ezekkel áramerősség nem mérhető) és egy változtatható ellenállás.   a) Határozzuk meg a lehető legkevesebb áramkör összeállításával az áramforrás elektromotoros erejét! Ehhez a méréshez csak a két voltmérő használható. (A változtatható ellenállás nem.) b) Most csak az egyik voltmérő és a változtatható ellenállás használható. Az előző ponttól független méréssel határozzuk meg az áramforrás elektromotoros erejét, az áramforrás és a voltmérő belső ellenállását! Ebből a célból célszerű a mérési eredmények alapján két grafikont készíteni, amelyeknek elméletileg egyenest kell adniuk, és a keresett mennyiségeket ezek segítségével meghatározni. c) Adjuk meg a hibaforrásokat! Melyek azok, amelyek leginkább befolyásolják a végeredményt?   Megoldás. $a)$ Készítsünk el két kapcsolást! Először a két feszültségmérőt sorbakötve kapcsoljuk az áramforrásra. Ekkor a műszerek $U_1$ és $U_2$ feszültséget mutatnak. A másik kapcsolásban csak az egyik feszültségmérőt kötjük az áramforrásra, és ekkor $U{\text{'}}_2$ feszültséget mérünk. $E$-vel és $r$-rel jelölve az áramforrás elektromotoros erejét és belső ellenállását, valamint $R_1$ és $R_2$-vel a két műszer belső ellenállását, a következőket írhatjuk fel: $\begin{array}{c}{\displaystyle \frac{U_1}{E}=\frac{R_1}{R_1+R_2+r}\mathrm{,}\frac{U_2}{E}=\frac{R_2}{R_1+R_2+r}\mathrm{,}\frac{U_2}{E}=\frac{R_2}{R_2+r}\mathrm{.}}\end{array}$ A három egyenletet rendezve kapjuk a keresett összefüggést: $\begin{array}{c}{\displaystyle E=\frac{U_{1}U{\text{'}}_2}{U{\text{'}}_2-U_2}\mathrm{.}}\end{array}$ $b)$ Ismét két kapcsolást készítsünk! Először a feszültségmérőt és a változtatható ellenállást sorosan kötve kapcsoljuk az áramforrásra. Ha $R_f$-fel, ill. $R$-rel jelöljük a feszültségmérő, ill. a változtatható ellenállás ellenállását, akkor az Ohm‐törvény felhasználásával a következő kifejezést kapjuk: $\begin{array}{c}{\displaystyle \frac{1}{U}=\frac{R_f+r+R}{E{R}_f}\mathrm{.}}\end{array}$ Ha a mért $U$ és $R$ értékek alapján az $1/U$-t ábrázoljuk az $R$ függvényében, akkor olyan pontokat kell kapnunk, amelyek egy egyenesre illeszkednek. Az egyenes $p_1=\frac{1}{E{R}_f}$ meredekségét és az ordinátával való $b=\frac{R_f+r}{E{R}_f}$ metszéspontját leolvashatjuk a grafikonról. A második kapcsolásban a voltmérőt és a változtatható ellenállást párhuzamosan kötve kapcsoljuk az áramforrásra. Ekkor $\begin{array}{c}{\displaystyle \frac{1}{U}=\frac{1+\left(1/R_f+1/R\right)r}{E}\mathrm{.}}\end{array}$ Most tehát ha az $1/R$ függvényében ábrázoljuk az $1/U$-t olyan pontokat kell kapnunk, amelyek a $p_2=r/E$ meredekségű egyenesre illeszkednek. A $p_1$, $p_2$ és $b$-re felírt összefüggésből a $p_1{p}_2{E}^2-bE+1=0$ egyenletet kapjuk, ahonnan $\begin{array}{c}{\displaystyle E=\frac{b\pm \sqrt[]{b^2-4p_1{p}_2}}{2p_1{p}_2}\mathrm{.}}\end{array}$ $p_1$, $p_2$ és $b$ meghatározása után tehát $E$-t kiszámíthatjuk. A keresett másik két mennyiséget az $R_f=1/E{p}_1$ és $r=E{p}_2$ összefüggések alapján kapjuk. $c)$ A mérés legjelentősebb hibáját a feszültségmérő pontatlansága okozza. Ez a hiba a képletekbe való behelyettesítéskor megsokszorozódik. (20 pont)