Cím:	1983. évi fizika OKTV feladatai
Szerző(k):	Bodó Zalán ,  Légrádi Imre ,  Nagy László ,  Vermes Miklós
Füzet:	1983/október, 81 - 86. oldal	PDF  |  MathML
Témakör(ök):	OKTV

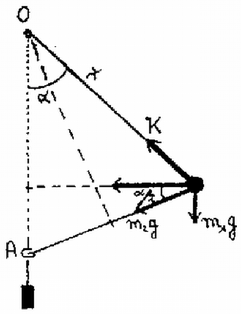
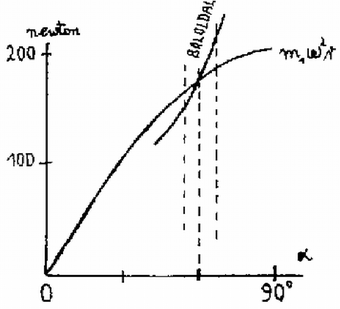
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az 1983. évi középiskolai tanulmányi verseny feladatai   Az I. forduló feladatai   1. Egy $m=8\text{<span style="font-style: italic;"> kg</span>}$ tömegű, belül üres, merev falú gömbbe egy másik, ugyancsak $m=8\text{<span style="font-style: italic;"> kg</span>}$ tömegű tömör, kis gömböt helyezünk (1. ábra). A gömböket levegőben, nagy magasságból leejtjük. A közegellenállási erő arányos a sebesség négyzetével: $F=k{v}^2$. Az arányossági szorzó m/s és newton esetében $k=0\mathrm{,}1$. Ábrázoljuk a kis gömb által a nagy gömbre kifejtett erőt a sebesség függvényében! $g=10{\text{ m/s}}^2$.  (Légrádi Imre) 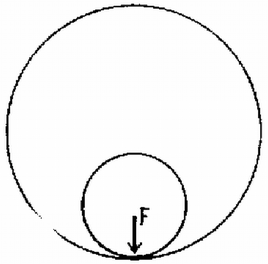  1. ábra 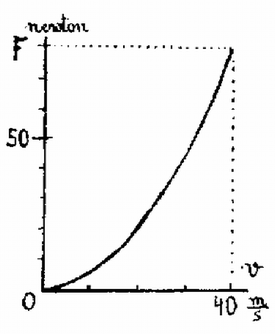  Megoldás. Az összesen 16 kg-ot gyorsító erő $16g-0\mathrm{,}1v^2$, a gyorsítandó tömeg 16 kg, tehát a közös gyorsulás $a=g-0\mathrm{,}00625v^2$. Az az erő, amellyel a 8 kg tömegű kis golyó a nagyot nyomja (hasonlóan a fonálerőhöz): $\begin{array}{c}{\displaystyle 8g-8\left(g-0\mathrm{,}00625v^2\right)=0\mathrm{,}05v^2\mathrm{.}}\end{array}$ A görbe parabola. Nulla sebességnél a golyók még éppen együtt esnek, a nyomóerő nulla. Határesetben akkor egyenletes a golyók mozgása, amikor $160=0\mathrm{,}1v^2$, vagyis $v=40$ m/s. Ekkor a nyomóerő a kis golyó teljes súlya, vagyis 80 newton.   2. Egy $r=0\mathrm{,}5\text{<span style="font-style: italic;"> m</span>}$ hosszú fonálra erősített $m_1=4\text{<span style="font-style: italic;"> kg</span>}$ tömegű test vízszintes síkban körpályán kering (2. ábra). Az inga fonala a függőlegessel $\alpha ={60}^{\circ }$-os szöget zár be. Az $m_1$ tömegű testhez erősített második fonalat az $A$-ban elhelyezett gyűrűn vetjük át; ezen a fonálon $m_2=6\text{<span style="font-style: italic;"> kg</span>}$ tömegű test lóg. $OA=r=0\mathrm{,}5$ m, $g=10$ m/s.   a) Mekkora a szögsebesség? b) Vizsgáljuk meg ezt a helyzetet a stabilitás szempontjából!  (Vermes Miklós) 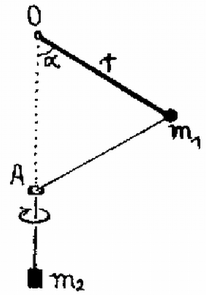    2. ábra 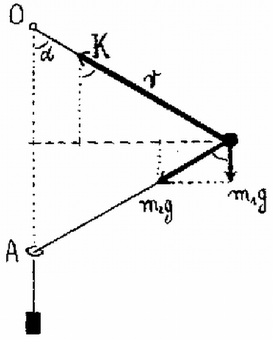  Megoldás. A felső kötélszárban $K$ erő hat (3. ábra).   3. ábra   Az $m_1$ tömegű testre ható erők függőleges összetevőinek egyensúlyfeltétele: $\begin{array}{c}{\displaystyle K\text{cos}\alpha =m_{1}g+m_{2}g\text{cos}\alpha \mathrm{.}}\end{array}$ A körmozgáshoz szükséges erőt a vízszintes összetevők összege szolgáltatja: $\begin{array}{c}{\displaystyle K\text{sin}\alpha +m_{2}g\text{sin}\alpha =m_1{\omega }^{2}r\text{sin}\alpha \mathrm{.}}\end{array}$ Az egyenletrendszer megoldása: $\begin{array}{c}{\displaystyle K=m_{2}g+\frac{m_{1}g}{\text{cos}\alpha }=140\text{ N}\mathrm{,}\omega =\sqrt[]{\frac{2m_{2}g}{m_{1}r}+\frac{g}{r\text{cos}\alpha }}=10{\text{ s}}^{-1}\mathrm{.}}\end{array}$ A stabilitás megvizsgálása mozgásban levő szerkezet esetében nem olyan egyértelmű, mint a statikában. Meg kell állapodnunk abban, hogy a vizsgálatot milyenfajta zavar esetében végezzük el. Ha a zavar a lelógó fonál meghúzásából ered, akkor a változás közben állandó marad az impulzusnyomaték és erre a feltételre ekkor tekintettel kell lennünk. Nézzük a legegyszerűbb esetet, amikor a szerkezetet egy gépezet állandóan $\omega =10{\text{ s}}^{-1}$ szögsebességgel tartja forgásban (ekkor az impulzusnyomaték nem marad változatlan). Megvizsgáljuk, hogyan alakul az erők egyensúlya, ha valamilyen külső ok megváltoztatja az $\alpha$ szöget (4. ábra). 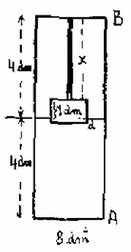4. ábra Nem speciálisan ${60}^{\circ }$-os, hanem tetszőleges $\alpha$ szögre végezzük el a számítást. A körmozgáshoz szükséges erő így alakul: $\begin{array}{c}{\displaystyle K\text{sin}\alpha +m_{2}g\text{cos}\frac{\alpha }{2}=m_1{\omega }^{2}r\text{sin}\alpha \mathrm{.}}\end{array}$ A $K$ kötélerőnek akkorának kell lennie, hogy biztosítva legyen a függőleges erőösszetevők egyensúlya is: $\begin{array}{c}{\displaystyle K\text{cos}\alpha =m_{1}g+m_{2}g\text{sin}\frac{\alpha }{2}\mathrm{.}}\end{array}$ Az ebből adódó $K$-t a körmozgásnál felhasználva következik az egyensúly feltétele: $\begin{array}{c}{\displaystyle m_{1}g\text{tg}\alpha +2m_{2}g\text{tg}\alpha \cdot \text{sin}\frac{\alpha }{2}=m_1{\omega }^{2}r\text{sin}\alpha \mathrm{.}}\end{array}$ A bal oldal menetét feltüntető görbe a jobb oldali szinuszgörbét $\alpha ={60}^{\circ }$-nál metszi, amint azt tudjuk. Az ábra görbéinek menetéből látszik, hogy az egyensúlyi helyzetet elrontva az erők törekvése az eredeti állapot visszaállítása. Ténylegesen elvégezve a kísérletet az $m_1$ tömegű test kúpingaszerűen keringene.   3. Egy $8{\text{<span style="font-style: italic;"> dm</span>}}^2$ alapterületű, $8\text{<span style="font-style: italic;"> dm</span>}$ magas henger alakú zárt edényben egy rugó tart a vízen lebegve egy téglatestet (5. ábra a). A téglatest tömege $2\text{<span style="font-style: italic;"> kg</span>}$, alapterülete $4{\text{<span style="font-style: italic;"> dm</span>}}^2$, magassága $1\text{<span style="font-style: italic;"> dm</span>}$. A rugó eredeti hossza $3\text{<span style="font-style: italic;"> dm</span>}$, rugóállandója $40\text{<span style="font-style: italic;"> N/dm</span>}$. A víz szintje az edény fele magasságában van. $g=10{\text{<span style="font-style: italic;"> m/s</span>}}^2$.   a) Milyen hosszú most a rugó? b) Milyen hosszú lesz a rugó, ha az edényt megfordítjuk, vagyis $A$ lapja helyett $B$ lapjára állítjuk?  (Vermes Milkós)   Megoldás. Az 5. ábra $a$ esetében a rugó hossza $x$, megnyúlása $x-3$, felhúzóereje $40\left(x-3\right)$. A téglatest bemerülése $d=x+1-4=x-3$, a hidrosztatikai felhajtóerő $4\left(x-3\right)\varrho g=40\left(x-3\right)$. A téglatest súlya 20 newton. Az erők egyensúlya folytán: $\begin{array}{c}{\displaystyle 20=40\left(x-3\right)+40\left(x-3\right)\mathrm{.}}\end{array}$ Innen a rugó mostani hossza $x=3\mathrm{,}25$ dm és a bemerülés $d=0\mathrm{,}25$ dm. Meg kell állapítanunk a víz mennyiségét: $\begin{array}{c}{\displaystyle 8\cdot 3\mathrm{,}75+4\cdot 0\mathrm{,}25=31{\text{ dm}}^3\mathrm{.}}\end{array}$ a. b. c. d. 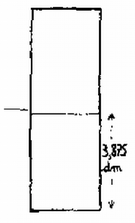5. ábra Téglatest nélkül (5. ábra $b$) a víz $3\mathrm{,}875$ dm magasan állna az edényben. Ha most ráhelyezzük a $0\mathrm{,}5{\text{ kg/dm}}^3$ sűrűségű téglatestet, az félig bemerülve úszik és a vízmagasság $4\mathrm{,}125$ dm. (c.) Ha most a téglatestet a fenékhez rögzített rugóhoz erősítjük, akkor a rugó lefelé húzza. Ebben az esetben a rugó hossza $y$ és a bemerülés $z$ (d.). Az erők egyensúlya: $\begin{array}{c}{\displaystyle 20+40\left(y-3\right)=40z\mathrm{.}}\end{array}$ A második egyenletet a vízmennyiség állandósága adja: $\begin{array}{c}{\displaystyle 31=8y+4z\mathrm{.}}\end{array}$ Az egyenletrendszer megoldása: $y=3\frac{5}{12}$ dm, $z=\frac{11}{12}$ dm, azaz a rugó hossza ekkor $3\frac{5}{12}$ dm.   4. Egy tartály fenekén $A=10{\text{<span style="font-style: italic;"> cm</span>}}^2$ nagyságú lyuk van (6. ábra). A lyukhoz egy rugó egy szelepet szorít hozzá, amely csak $F=6\mathrm{,}5\text{<span style="font-style: italic;"> N</span>}$-nál nagyobb erő esetében nyílik ki. A tartályba $0\mathrm{,}5\text{<span style="font-style: italic;"> m</span>}$ magasan vizet öntünk, majd a tartályt függőlegesen rezgő mozgásba hozzuk. A rezgés amplitúdója $r=0\mathrm{,}05\text{<span style="font-style: italic;"> m</span>}$, körfrekvenciája $\omega =12{\text{<span style="font-style: italic;"> s</span>}}^{-1}$. Milyen magas vízoszlop marad végül is a tartályban? $g=10{\text{<span style="font-style: italic;"> m/s</span>}}^2$.    (Nagy László) 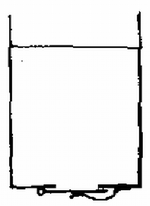    6. ábra   Megoldás. A vízoszlopnak akkor maximális a gyorsulása, amikor a legalsó helyzetben van: $\begin{array}{c}{\displaystyle a_m=r{\omega }^2=7\mathrm{,}2{\text{ m/s}}^2\mathrm{.}}\end{array}$ Legalul a szelepet nyomja az $x$ magasságú, $\varrho$ sűrűségű megmaradt vízoszlop súlya és a rezgésből származó erő: $\begin{array}{c}{\displaystyle Ax\varrho g+r{\omega }^{2}Ax\varrho =Ax\varrho \left(g+r{\omega }^2\right)\mathrm{.}}\end{array}$ Ezzel egyenlő a szelepet nyitó erő: $\begin{array}{c}{\displaystyle F=Ax\varrho \left(g+r{\omega }^2\right)\mathrm{.}}\end{array}$ Innen a megmaradó vízoszlop magassága: $\begin{array}{c}{\displaystyle x=\frac{F}{A\varrho \left(g+r{\omega }^2\right)}=0\mathrm{,}38\text{ m}\mathrm{.}}\end{array}$   A II. forduló feladatai   1. Egy korong állandó szögsebességgel forog függőleges tengelye körül (7. ábra). A korongra egy $L=1\text{<span style="font-style: italic;"> m</span>}$ hosszú lécet támasztottunk és ez a koronggal együtt forog. A léc alsó vége $r=0\mathrm{,}8\text{<span style="font-style: italic;"> m</span>}$-re van a tengelytől, felső vége épp a tengely felett van. Mennyi a korong szögsebessége? $g=10{\text{<span style="font-style: italic;"> m/s</span>}}^2$.  (Nagy László) 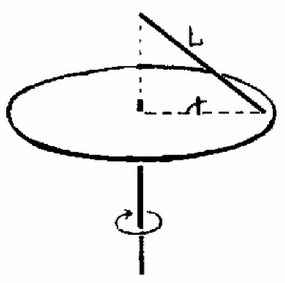    7. ábra 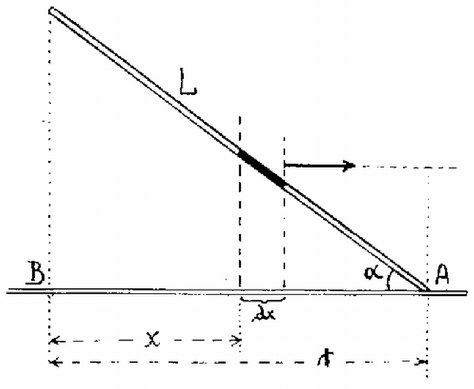  Megoldás. A pálca egységnyi hosszúságú darabjának tömege $\sigma$, a $dx$ vetületű, $x$ távolságban levő darabjának tömege $\sigma dx/\text{cos}\alpha$. E rész körmozgásához $\varrho dx\cdot {\omega }^2\cdot x/\text{cos}\alpha$ erő szükséges (8. ábra).   8. ábra   Számítsuk ki a forgatónyomatékok egyenlőségét a pálca $A$ alátámasztási pontjára vonatkozóan! A $dx$ vetületű darab forgatónyomatéka: $\begin{array}{c}{\displaystyle \frac{\sigma dx}{\text{cos}\alpha }{\omega }^{2}x\left(r-x\right)\text{tg}\alpha \mathrm{.}}\end{array}$ A teljes forgatónyomaték: $\begin{array}{c}{\displaystyle \underset{0}{\overset{r}{\int }}\frac{\sigma {\omega }^2\text{tg}\alpha }{\text{cos}\alpha }\left(rx-x^2\right)dx=\frac{\sigma {\omega }^2\text{tg}\alpha r^3}{6\text{cos}\alpha }\mathrm{.}}\end{array}$ \epsfbox{1983‐84‐2.eps}8. ábra Az egész pálca tömege $m=\sigma r/\text{cos}\alpha$, ezért a számított forgatónyomaték: $\begin{array}{c}{\displaystyle \frac{m{\omega }^2\text{tg}\alpha r^2}{6}\mathrm{.}}\end{array}$ A súly lebillentő forgatónyomatéka $mgr/2$. Egyenlővé téve: $\begin{array}{c}{\displaystyle \frac{m{\omega }^2{r}^2\text{tg}\alpha }{6}=\frac{mgr}{2}\mathrm{.}}\end{array}$ A keresett szögsebesség: $\begin{array}{c}{\displaystyle \omega =\sqrt[]{\frac{3g}{r\text{tg}\alpha }}=\sqrt[]{50}=7\mathrm{,}07{\text{ s}}^{-1}\mathrm{.}}\end{array}$ A pálca alsó vége a korongot függőlegesen $mg$ erővel nyomja. A vízszintes erő $mr{\omega }^2/2$, ami az elemi‐rúddarabok centripetális erő szükségletének az összege. Ezek eredőjének, a támaszerőnek a vízszintessel alkotott $\beta$ szöge: $\text{tg}\beta =2g/r{\omega }^2$, $\beta =26\mathrm{,}{57}^{\circ }$. Az $\alpha$ szög $36\mathrm{,}{87}^{\circ }$. A támaszerő iránya nem esik egybe a rúd irányával, nem megy át a rúd súlypontján.   2. Vízszintes asztallapon $r=0\mathrm{,}2\text{<span style="font-style: italic;"> m</span>}$ sugarú hengert rögzítettünk. Kerületéhez $L=0\mathrm{,}8\text{<span style="font-style: italic;"> m</span>}$ hosszú fonalat erősítettünk az érintő irányában (9. ábra). E fonál végén, az asztalon fekve $m=0\mathrm{,}6\text{<span style="font-style: italic;"> kg</span>}$ tömegű test van, amelyet a fonálra merőlegesen $v=0\mathrm{,}4\text{<span style="font-style: italic;"> m/s</span>}$ sebességgel elindítunk. A súrlódás elhanyagolható.   a) Mennyi idő múlva ér az $m$ tömegű test a hengerhez? b) Hogyan függ a fonalat feszítő erő az időtől?  (Dr. Bodó Zoltán) 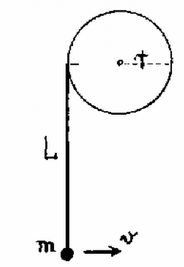    9. ábra   Megoldás. A sebesség mindig merőleges a fonálra, a fonálerő nem végez munkát, nem képes változtatni a sebességet, a test mindvégig $v=0\mathrm{,}4$ m/s sebességgel mozog. Ki kell számítani a pálya (kör‐evolvens) hosszát. A fonál érintési pontjaihoz rajzolt rádiuszok $d\phi$ szöget zárnak be (10. ábra). A fonál $r\cdot d\phi$ darabbal lett rövidebb: 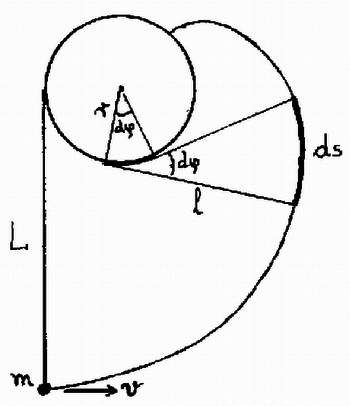$dl=-r\cdot d\phi$.   10. ábra   A pálya hosszának kis eleme: $ds=l\cdot d\phi$. Kiküszöbölve $d\phi$-t: $\begin{array}{c}{\displaystyle ds=-\frac{l}{r}\cdot dl\mathrm{.}}\end{array}$ Az egész út: $s=-\underset{L}{\overset{0}{\int }}\frac{l}{r}dl=\frac{L^2}{2r}=1\mathrm{,}6$ m. A mozgás időtartama: $\begin{array}{c}{\displaystyle T=\frac{L^2}{2rv}=4\text{ s}\mathrm{.}}\end{array}$ A pillanatnyi pályasugár $l$, a forgási középpont felé mutató erő $m{v}^2/l$. Meg kell állapítani hogyan függ $l$ az időtől. Az út kiszámításánál $l$-től nem 0-ig, hanem egy tetszőleges $l$-ig integrálunk; ez az út $s=vt$: $\begin{array}{c}{\displaystyle s=-\underset{L}{\overset{l}{\int }}\frac{l}{r}dl=\frac{1}{2r}\left(L^2-l^2\right)=vt\mathrm{.}}\end{array}$ Ebből $\begin{array}{c}{\displaystyle l=\sqrt[]{L^2-2rvt}\mathrm{.}}\end{array}$ Az erő, mint az idő függvénye: $\begin{array}{c}{\displaystyle F=\frac{m{v}^2}{\sqrt[]{L^2-2rvt}}=\frac{0\mathrm{,}24}{\sqrt[]{4-t}}\mathrm{.}}\end{array}$ 3. Egy rögzített $Q=+1Q^{-15}\text{<span style="font-style: italic;"> C</span>}$ elektromos töltés felé nagyon messziről $v_0=200\text{<span style="font-style: italic;"> m/s</span>}$ sebességgel elindítunk egy $m=0\mathrm{,}01\text{<span style="font-style: italic;"> g</span>}$ tömegű, $q=+{10}^{-7}\text{<span style="font-style: italic;"> C</span>}$ töltésű apró golyócskát egy olyan egyenes mentén, amely $d=0\mathrm{,}1\text{<span style="font-style: italic;"> m</span>}$ távolságban van a $Q$ töltéstől (11. ábra).   a) Mekkora lesz a két töltés közötti legkisebb távolság? b) Mekkora legyen a $d$ távolság, hogy a $q$ töltésű test végső sebessége az eredeti $v_0$-ra merőleges legyen?     11. ábra 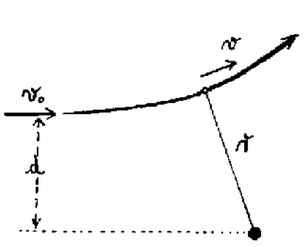  Megoldás. A négyzetes erőtörvény következtében a pálya hiperbola (12. ábra).   12. ábra   Az elektromos taszítóerő ellen végzett munka egyenlő a mozgási energia csökkenésével: $\begin{array}{c}{\displaystyle \frac{m{v}_0^2}{2}-\frac{m{v}^2}{2}=\frac{kqQ}{r}\mathrm{,}}\end{array}$ $k$ a Coulomb‐törvény arányossági szorzója, $k=9\cdot {10}^9$. A mozgó töltésre érvényes a területi sebesség állandósága. A területi sebesség induláskor $d{v}_0$, a legközelebbi helyzetben $rv$; $\begin{array}{c}{\displaystyle d{v}_0=rv\mathrm{.}}\end{array}$ $v$ kiküszöbölése után, rendezve: $\begin{array}{c}{\displaystyle \frac{m{v}_0^2}{2}\cdot r^2-kqQ\cdot r-\frac{m{v}_0^2{d}^2}{2}=0.}\end{array}$ Az egyenletrendszer megoldása: $\begin{array}{c}{\displaystyle r=\frac{kqQ}{m{v}_0^2}+\sqrt[]{{\left(\frac{kqQ}{m{v}_0^2}\right)}^2+d^2}=0\mathrm{,}125\text{ m}\mathrm{.}}\end{array}$ Továbbá $v=\frac{d}{r}\cdot v_0=160\text{ m/s}$.   A hiperbola legközelebbi, $A$ pontja a hiperbola csúcspontja (13. ábra). Az $AQ$ egyenesen fekszik a hiperbola $O$ centruma, ahol a kezdeti és végső sebességek irányai, az aszimptoták metszik egymást. $AO$ a hiperbola fél valós tengelye, $OQ$ pedig a fókusztávolsága. $OHQ$ és $OGA$ háromszögek egybevágóak. 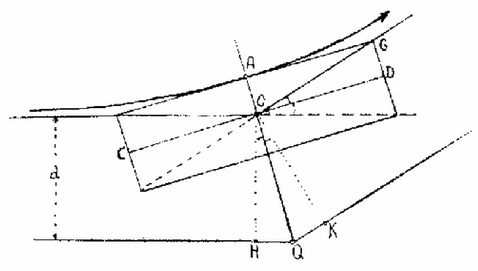  13. ábra   Így $OD=OH=d$ a hiperbola fél képzetes tengelye. A fókusztávolság $OQ=\sqrt[]{A{O}^2+d^2}$ a legrövidebb $r$ távolságunk pedig $AO+\sqrt[]{A{O}^2+d^2}$. Ebből következik, hogy bármekkora $v_0$ indítási sebesség mellett a hiperbola fél képzetes tengelye $d$, fél valós tengelye pedig $\begin{array}{c}{\displaystyle AO=\frac{kqQ}{m{v}_0^2}\mathrm{.}}\end{array}$ Az aszimptoták merőlegességének feltétele, hogy a valós és képzetes tengelyek egyenlők legyenek: $\begin{array}{c}{\displaystyle \frac{kqQ}{m{v}_0^2}=d\mathrm{.}}\end{array}$ Ebből a mi számadatainkkal $d=0\mathrm{,}0225\text{ m}$, $r=0\mathrm{,}05432\text{ m}$ és $v=82\mathrm{,}842$ m/s következik.   A III., kísérleti forduló   A versenyzők megismerkedtek a Fresnel‐féle zónalemez elméletével és mérőkísérleteket végeztek vele.