Kezdőlap


Cím:	1982. évi Eötvös Loránd Fizikaverseny
Füzet:	1983/február, 81. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat 1982. október 23-án rendezte 59. versenyét Budapesten és 11 vidéki városban az abban az évben érettségizettek és középiskolások részére. A versenyzők 5 órai munkaidő alatt oldhatták meg a húrom feladatot. Bármely segédeszköz, használata meg volt engedve, beleértve a zsebszámítógépet is. A versenyen 248 dolgozatot adtak be. Ismertetjük a feladatokat és a verseny eredményét.

1. Egy

r = 5

cm sugarú golyót

L = 6

cm hosszú fonállal egy fal mellé függesztünk. (1. ábra). Súrlódás nincs. A golyót úgy tartjuk, hogy a fonál éppen érintője legyen. Ezután a golyót elengedjük.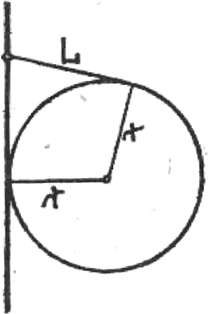

g = 10

m/s

^{2}

1. ábra

a) Mekkora szöggyorsulással indul el a golyó?
b.) Mekkora a mozgás folyamán a golyó legnagyobb szögsebessége?
(Vermes Miklós)

Megoldás. a) kérdés. Első módszer. A golyó mozgása közben a fonál golyóhoz erősített pontja

L

sugarú köríven, a golyó középpontja a fallal párhuzamos,

r

távolságban levő függőleges egyenesen mozog. A mozgást a golyó

O

középpontja körül történő forgás és középpontjának függőleges süllyedő mozgása összegének tekintjük. A fonálerő

F

, a súlyerő

m g

, a középpont süllyedésének függőleges gyorsulása

a

, a középpont körüli forgás szöggyorsulása

β

, a középpont körüli tehetetlenségi nyomaték

Θ = 0,4 m r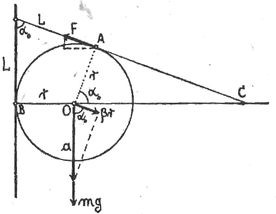^{2}

(2. ábra).

2. ábra

Newton II. törvénye a függőleges irányú erő-összetevőkre vonatkozóan:

\begin{matrix} m a = m g - F cos α_{0} . \end{matrix}

A forgás alaptörvénye szerint:

\begin{matrix} F r = β Θ . \end{matrix}

(A súlynak és a fal nyomóerejének nincs forgatónyomatéka az

O

pontra vonatkozóan.) A gömb

A

pontjának kerületi gyorsulása az

a

függőleges gyorsulás vetülete:

\begin{matrix} β r = a cos α_{0} . \end{matrix}

Az egyenletrendszer megoldása:

\begin{matrix} a = g \cdot \frac{1}{1 + Θ_{0} cos^{2} α_{0} / m r^{2}} = 9,871 m / s^{2} . \end{matrix}

\begin{matrix} F = m g \cdot \frac{Θ_{0} cos α_{0} / m r^{2}}{1 + Θ_{0} cos^{2} α_{0} / m r^{2}} = 0,0712 N . \end{matrix}

\begin{matrix} β = \frac{g}{r} \cdot \frac{cos α_{0}}{1 + Θ_{0} cos^{2} α_{0} / m r^{2}} = 35,60 s^{- 2} . \end{matrix}

Második módszer. Mivel

A

pont az

L

sugarú körív érintője mentén,

B

pont függőlegesen lefelé indul el, ezért az indulás pillanatában a pillanatnyi forgási középpont

C

. Induláskor a pillanatnyi forgási sugár:

\begin{matrix} O C = ϱ = \frac{r}{cos α_{o}} . \end{matrix}

C

pont körüli forgás forgatónyomatéka

m g ϱ = \frac{m g r}{cos α_{0}}

,
a

C

pontra vonatkozó tehetetlenségi nyomaték:

\begin{matrix} Θ = Θ_{0} + m ϱ^{2} = Θ_{0} + \frac{m r^{2}}{cos^{2} α_{0}} . \end{matrix}

C

pontban levő forgástengely szempontjából csak az

m g

súlyerő jelent forgatónyomatékot, amelynek erőkarja

ϱ

. A forgás törvénye szerint:

\begin{matrix} \frac{m g r}{cos^{2} α_{0}} = β (Θ_{0} + \frac{m r^{2}}{cos^{2} α_{0}}) . \end{matrix}

A keresett szöggyorsulás:

\begin{matrix} β = \frac{g}{r} \cdot \frac{cos α_{0}}{1 + Θ_{0} cos^{2} α_{0} / m r^{2}} = 35, 60 s^{- 2} . \end{matrix}

Egyébként az indulási

α_{0}

szögre levezethető, hogy

cos α_{0} = (L^{2} - r^{2}) / (L^{2} +

+ r^{2}) = 11 / 61 = 0, 1803

α = 79, 61^{\circ}

. A numerikus értékek úgy alakulnak, hogy az eredmény keveset változna, ha a feladat gömb helyett hengerről vagy abroncsról szólna.
b) kérdés. A gömb süllyedése közben a helyzeti energia alakul át mozgási energiává. Lényeges körülmény, hogy amikor a gömb eléri legmélyebb helyzetét, vagyis az

L

fonál és az

r

sugár egy egyenesbe esnek, akkor a gömb simán forog; ebben a pillanatban nem süllyed és nem rántja meg a fonalat, tehát a helyzeti energia csökkenése teljes egészében a forgás mozgási energiájává alakul (3. ábra).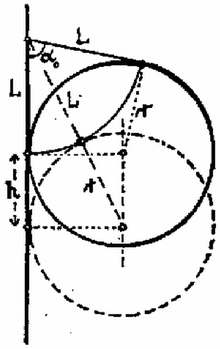

3. ábra

A súlypont süllyedése:

\begin{matrix} h = \sqrt[]{{(L + r)}^{2} - r^{2}} - L = \sqrt[]{2 L r + L^{2}} - L = 0, 038 méter . \end{matrix}

A helyzeti energia csökkenése egyenlő a megszerzett forgási energiával:

\begin{matrix} m g h = \frac{Θ_{0} ω^{2}}{2} . \end{matrix}

Innen a keresett szögsebesség:

\begin{matrix} ω = \sqrt[]{\frac{2 m g h}{Θ_{0}}} = 27, 56 s^{- 1} . \end{matrix}

A mechanikai energiamegmaradás törvénye alapján kiszámítható, hogy a nehézségi erő munkavégzése miként alakul át a középpont haladásának és a forgásnak mozgási energiájává. Az eredményt a 4. ábra mutatja.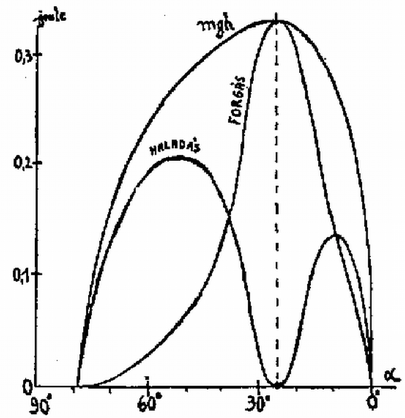

4. ábra

α_{0} = 79, 61^{\circ}

indulási helyzetből kiindulva a súlypont legmélyebb helyzetében

cos α = r / (r + L) = 5 / 11 = 0, 4545

α = 27, 04^{\circ}

, ekkor minden mozgási energia a forgás energiájaként jelentkezik. A végső helyzetben, amikor

α = 0

, a súlypont ugyanolyan magasságba kerül, mint ahonnan elindult, de most a fonál a fal mellett van. A haladó mozgás és forgás mozgási energiáinak összege minden helyzetben egyenlő a súlyerő

m g h

munkavégzésével.
Számítással, számítógéppel pillanatról pillanatra követni lehet a mozgás időbeli lefolyását. A számítás eredményét az 5. ábra mutatja.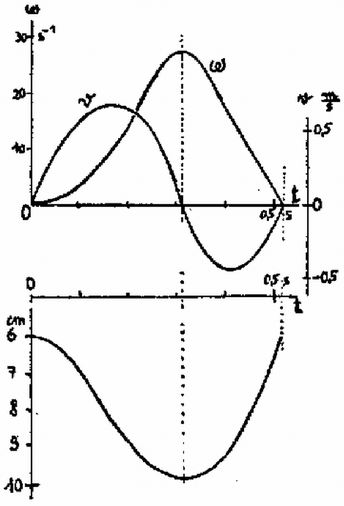

5. ábra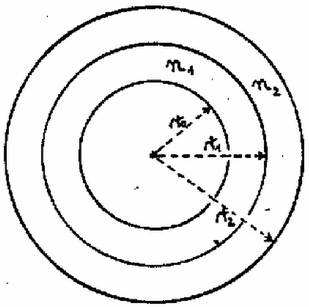

Az ábra felső része a sebesség és szögsebesség időbeli lefolyását mutatja. A középpont haladási mozgásának

v

sebessége egy maximum után

27, 04^{\circ}

-nál, a súlypont legmélyebb helyzeténél nulla; ekkor a szögsebesség maximális. Ez körülbelül

0, 31

másodperckor következik be. Ezután a súlypont haladási sebessége irányt változtat. Az eredeti magasság kb.

0, 52

másodperc múlva következik be. Az ábra alsó része a golyó középpontjának mélységét mutatja az idő függvényében.

6. ábra

2. Egy

r_{0} = 6 cm

sugarú fémhengert két átlátszó hengergyűrű vesz körül koncentrikusan (6. ábra). Az elsőnek a sugara

r_{1} = 9 cm

és törésmutatója

n_{1} = 4 / 3

, a másodiknak a sugara

r_{2} = 12 cm

és törésmutatója

n_{2} = 1, 5

. Milyen vastagnak látszik a fémhenger, ha nagy távolságból nézzük az átlátszó rétegeken keresztül?
(Vermes Miklós)

Megoldás. A nagy távolságból való nézés azt jelenti, hogy a fémhenger mellett érintőlegesen elhaladó fénysugarak párhuzamosan érkeznek szemünkbe (7. ábra).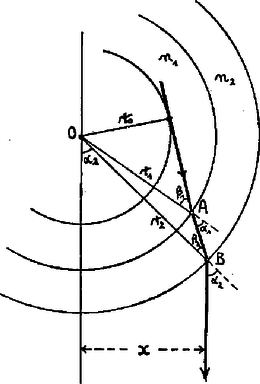

7. ábra

A fémhenger sugarának látszólagos hossza:

x = r_{2} sin α_{2}

. A

B

pontban végbemenő törésnél

sin α_{2} / sin β_{2} = n_{2}

, vagyis a látszólag megvastagodott sugár

x = r_{2} n_{2} sin β_{2}

.
Az

A O B

háromszögben a szinusz‐tétel szerint igaz:

\begin{matrix} \frac{sin β_{2}}{sin α_{1}} = \frac{r_{1}}{r_{2}}, \end{matrix}

és így

sin β_{2} = r_{1} sin α_{1} / r_{2}

.

Ezzel a fémhenger látszólagos rádiusza:

\begin{matrix} x = r_{2} n_{2} \cdot \frac{r_{1} sin α_{1}}{r_{2}} = n_{2} r_{1} s i n α_{1} . \end{matrix}

Végül az

A

pontban végbemenő törésnél

sin α_{1} / sin β_{1} = n_{1} / n_{2}

, tehát

sin α_{1} = n_{1} sin β_{1} / n_{2}

. A látszólagos rádiusz:

\begin{matrix} x = n_{2} r_{1} \cdot \frac{n_{1} sin β_{1}}{n_{2}} = n_{1} r_{1} sin β_{1} . \end{matrix}

A legbelső derékszögű háromszögből

sin β_{1} = r_{0} / r_{1}

és így a végeredmény:

\begin{matrix} x = n_{1} r_{1} \cdot \frac{r_{0}}{r_{1}} = n_{1} r_{0} = 8 cm . \end{matrix}

Mindez akkor érvényes, ha a rádiuszok elég nagyok ahhoz, hogy a megnövekedetten látszó

r_{0}

beléjük férjen.
Nevezetes dolog, hogy az eredmény teljesen független a gyűrűk sugarának nagyságától és csak a legbelső gyűrű törésmutatójától függ. Az eredmény független a törésmutatók nagyságbeli sorrendjétől is. Az eredmény ugyanígy érvényes tetszőleges számú gyűrű esetében is. Ha a legbelső gyűrű levegő, akkor bármilyenek legyenek is a külső gyűrűk, a fémhenger eredeti vastagságában látszik. Mindez kísérletileg könnyen ellenőrizhető.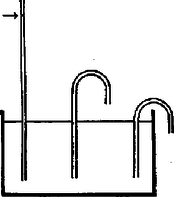

8. ábra

3. A 8. ábrán látható, folyadékba merülő három kapilláris cső anyaga és keresztmetszete pontosan egyforma. Az első kapillárisban az ábrán látható magasságig emelkedik fel a folyadék. Hogyan viselkedik a folyadék a másik két kapillárisban?
(Károlyházy Frigyes)

Megoldás. Adott anyagi minőségek és átmérő mellett a felületi feszültség egy adott magasságú folyadékoszlop hidrosztatikai nyomását képes ellensúlyozni. A felületi feszültség által létrehozott nyomás mindig a felszín homorú oldala felé irányul. Amikor a cső folyadékon kívül levő vége az edényben levő folyadékszint felett van, akkor a felszín, a meniszkusz befelé homorú, hogy a felületi feszültségből származó erő felhúzza a folyadékot a cső nyitott végének magasságáig (9. ábra).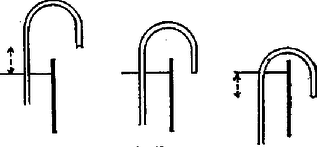

9. ábra

Ha a cső külső vége az edény folyadékszintjének magasságában van, akkor a felszín sík, nincs ellensúlyozni való hidrosztatikai nyomáskülönbség. Ha a cső külső vége lejjebb van az edény folyadékszintjénél, akkor a meniszkusz kifelé domború, hogy visszanyomja a folyadékot a hidrosztatikai nyomás ellenében. Természetesen csak akkora hidrosztatikai nyomásokat képes a felületi feszültség kiegyensúlyozni, amelyek a 8. ábra első csövének folyadékszintjéből következőnél kisebbek.
Érdemes az illeszkedési szög problémájával foglalkozni (10. ábra).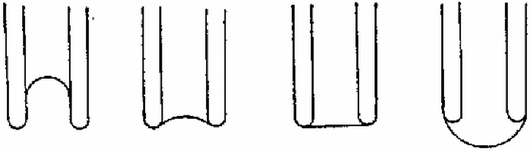

10. ábra

Adott folyadék és fal esetében a folyadékfelszínnek a fallal alkotott szöge egy adott érték, amely nem függ a fal helyzetétől. A 10. ábra négy esetet tüntet fel, a függőleges, párhuzamos vonalpárok a cső falait mutatják, legömbölyített végekkel. Az első esetben a szabad csővég az edény folyadékszintje fölött van, a meniszkusz a legnagyobb görbületet, legkisebb rádiuszt mutatja, mert nagy nyomáskülönbség kiegyensúlyozására van szükség. Süllyesztve a szabad csővéget a meniszkusz kevésbé görbült lesz. Egyenlő szintkülönbség esetében a felszín sík. Végül a belső folyadékszint alá süllyesztve a szabad csővéget, a meniszkusz kifelé görbül. De mind a négy esetben a folyadék illeszkedési szöge az üveghez nulla, a víz nedvesíti az üveget.

A verseny eredménye

I. díjat hárman nyertek egyenlő helyezésben: Csörgő Tamás, az ELTE fizikus hallgatója, aki Gyöngyösön a Berze Nagy János Gimnáziumban érettségizett mint Kiss Lajos tanítványa, Erdős László, a budapesti Berzsenyi Dániel Gimnázium III. osztályos tanulója (tanára Koltai Márta) és Tóth Gábor, a budapesti Fazekas Mihály Gimnázium IV. osztályos tanulója (tanára Horváth Gábor). II. díjat nyert Jeney Tamás honvéd, aki Miskolcon a Földes Ferenc Gimnáziumban érettségizett mint Zsudel László és Zámborszky Ferenc tanítványa. III. díjat nyertek egyenlő helyezésben: Károlyi Gyula, az ELTE matematikus hallgatója, aki Budapesten a Fazekas Mihály Gimnáziumban érettségizett mint Horváth Gábor tanítványa és Megyesi Gábor, a szegedi Ságvári Endre Gimnázium 11. osztályos tanulója (tanára Juhászné Mészáros Mária). Dicséretet hárman kaptak egyenlő helyezésben: Fodor Zoltán, az ELTE fizikus hallgatója, aki Budapesten a Teleki Blanka Gimnáziumban érettségizett, tanára Tomcsányi Péter volt, Mogyorósi András, a Semmelweis Orvostudományi Egyetem hallgatója, aki Vácott a Sztáron Sándor Gimnáziumban érettségizett mint Skripeczky Gyula és Dániel Gyula tanítványa és Oszlányi Gábor honvéd, aki Miskolcon érettségizett a Földes Ferenc Gimnáziumban mint Zámborszky Ferenc tanítványa.