Cím: A természet játékai - Káosz
Szerző(k):  Marx György 
Füzet: 1983/december, 193. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Cél. A determinisztikus mozgástörvényeket megtestesítő differenciálegyenletek azt ígérik, hogy kiszámítható a jövő, azt egyértelműen determinálja a jelen. A populációbiológia szaporodási törvényét is ilyen differenciálegyenlettel modellezték. Ennek a törvénynek a matematikai vizsgálata azonban váratlan és meglepő fordulatra vezetett, melynek elemzése túlnyúlik a biológián, és az egész természet-leírásra vonatkozóan elgondolkodtató tanulságot kínál.
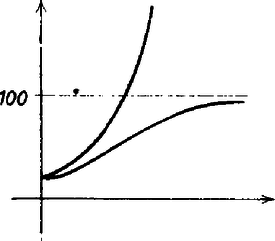
Nyulak élnek egy szigeten. Egy nyúlnak évente C kölyke van. Egy-egy év alatt az x(t) nyúllétszám

dxdt=Cx
értékkel változik. A differenciálegyenlet megoldása
x(t)=x(0)⋅eCt,
(exponenciális szaporodás). A sziget azonban nem képes akárhány nyulat eltartani, hanem - mondjuk - csak 100 állatot. A telítődő élettér a nyulakban kifejlődött genetikai program szerint a kölykök számának csökkenéséhez vezet. x populációlétszám esetén az élettér (100-x)/100 hányada szabad, a kölykök száma ezzel lesz arányos:
C(t)=C⋅100-x(t)100,
ami a következő differenciálegyenletre vezet:
dxdt=C⋅100-x100x.(1)
Ennek megoldása
x(t)=1001+A⋅e-Ct.
Ez a függvény az x(0)=(1+A)-1 értékről indul, és t→∞ esetén növekvőleg az x(∞)=100 határértékhez simul. A görbét a populációbiológiában logisztikus görbeként ismerik.
De a nyulak nem tanultak integrálszámítást. Az állatok az év bizonyos szakaszában (vagy szakaszaiban) kölykedznek, így a populációlétszám véges lépésekben, generációkban változik.
 

Játék. Nyulak élnek egy szigeten. Egy nyúlnak generációnként átlagosan K kölyke van. Így a nyúlpopuláció létszámának alakulása évről évre a következő összefüggéssel írható le:
xn+1=xn+K⋅xn.(2)
A nyúlpopuláció létszáma tehát mértani sorozatként "robban fel'' : xn=x0⋅(1+K)n. De a sziget nem képes akármennyi nyulat eltartani, hordozókapacítása legyen 100 nyúl. Ha kevesebben vannak, szaporodnak. Ha többen, éhen halnak. A nyulak genetikai programja ezt figyelembe veszi, a kölykök száma a nyitva álló élettérrel arányosan változik: tehát
xn+1=xn+K100(100-xn)xn.(3)

Induljunk x0=2 nyúllal. A játék elején a játékosok fogadjanak: mekkora legyen K, hogy a nyúlnépesség a leghamarabb elérje az x=99 és 101 közé eső telítődési értéket? (Javasoljuk, hogy a  K=0,5;1;1,5;2;2,5;3;3,5;4 értékekkel próbálkozzanak. Ezek "kézenfekvő'' értékek, hiszen egy nyúlpárra vonatkozóan ezek adnak egész számú kölyköt.) Induljon el a számolás! Minden versenyző jegyezze fel, hogy hány nyúl lesz az egymást követő generációkban!
 

Számológép. Programozható számológéppel (PTK-1072, PTK-1050) kényelmesebb a játék. A PTK 1072 gépen az M0 rekeszben lesz a mindenkori nyúllétszám, M1-ben az évszám, M9-ben pedig a kölykök számának századrésze. LD! A gép a következő évi nyúlpopulációt számítja ki elsőként:
MR0+(MR9*MR0*(100-MR0))=M0,
majd M1-hez egyet hozzáad, végül kiírja a nyúllétszámot egészekben, sőt a tizedesponttól jobbra az évek számát is feltünteti:
1  FM+1 NR0 F INT+(.01*MR1) = R/S  GOTO 00
RUN! Évenkénti szaporulat ÷100 az M9-be. Kezdeti nyúllétszám: M0. Indítás: F FP 2, GOTO 00, R/S.
A PTK 1050 esetében a Σ+ statisztikai funkciót használtuk fel az összegzésre és a Pause segítségével jelezzük ki az évek számát. Kezelése: RST, évenkénti szaporulat, R/S, majd az évek és a nyúllétszám leolvasása után újból R/S stb.
Gyakran előfordul, hogy a (3) egyenlet valamelyik esztendő nyúlpopulációjára negatív vagy 0 értéket ad. Tisztán formális szempontból ez nem hiba, a program tovább futna. Hogy ezt elkerüljük, a programba a kijelzés után egy feltételes elágazást iktatunk, amely a negatív vagy 0 létszámú kísértetnépesség továbbszaporítására irányuló törekvésünk hiábavalóságára egy akasztófával (PTK 1072) figyelmeztet. (A negatív szám logaritmusának keresésekor jelentkező, gépbe épített hibajelzést használtuk fel.)
 

PTK 1050  00  ÷     10    STO 0    20    RCL 1    30    2nd x  ≧  t  01    1    11    2nd Fix 0    21  *     31    GTO 1  02    0    12  2nd Lbl 1    22    RCL 6    32yx  03    0  13    1    23  =    33    1  04    =    14    0    24    2nd  Σ+    34  =  05    STO 6    15    0    25    2nd Pause0  06    3    16    -  26    1  0  07    0    17    RCL 1    27    x=t  0  08    STO 1    18    =    28    RCL 1  0  09    CLR    19  *     29    R/S  0

 

PTK  1072  00    MR    10  (    20    M    30    +    40    R/S    01    0    11    1  21    0    31  (    41    -  02    +    12    0    22    1    32  .  421    03  (  13    0    23  F    33    0    43    =  04    MR    14    -    24    M+    34  1    44    SKIP  05    9    15    MR    25    1  35  *     45    GOTO  06  *     16  0 -  26    MR    36    MR    46    0  07    MR    17  )    27    0  37    1    47    0  08    0    18  )    28    F    38  )    48    LN  09  *     19    =    29    INT    39    =  0   0   

 

Számítógép még gyorsabb, sőt a képernyőre fel is rajzolja a nyúlnépesség alakulását.
  10    PRINT "MEKKORA LEGYEN K";  20    INPUT K  30    CLS  40    LET X=2  50    FOR T=1 TO 60  60    LET X=X+.  01*K*X*(100-X)  70    IF  X<0  THEN 120  80    PLOT T,X/4  90    PRINT AT 0,0;T; "GENERACIO TELT EL"  100    NEXT T  110    GOTO 10  120    PRINT AT 2,0; "KIHALTAK A NYULAK"  130    GOTO 10

 

A K értékét érdemes egymás után a következőknek választani:
 

K=0,5,1,1,5,1,7,1,99 konvergencia
K=2,2,2,4  bifurkácio
K=2,5 4-szeres bifurkácio
K=2,7,2,8,2,99  káosz
K=3,01  kihalás.
 

Matematika. Mennyi lehet
xxx...?
Pontosabban, van-e az
xn+1=(x0)xn(4)
iterációs képlettel meghatározott sorozatnak határértéke a n→∞ esetén? Kalkulátor és számítógép egyaránt mutatja, hogy 1,4446 felett a sorozat divergál, az alatt pedig konvergál. Amint x0 csökkenni kezd, mégpedig jóval 1 alá, a határértéket nem monoton közelíti meg a sorozat, hanem oszcillácion át (csillapított határciklus), de a határérték létezik. Érdekes és váratlan dolgot tapasztalunk azonban x0<0,066 esetén. Nincs határérték, hanem elég sok lépés után az egymást követő xn értékek két szám, a és b között ugrálnak (csillapítatlan határciklus).* Ha x0→+0, akkor  a→1 és b→0. A határérték eme villaszerű szétágazását a "vezérlő paraméter'' (esetünkben x0 ) egy bizonyos értékétől kezdve, a villa latin nevéről bifurkációnak nevezik. A (4) sorozat az egyszerű bifurkáció tipikus példája.
A matematikusok - a struktúrák kialakulásának törvényei után kutatva - élénken érdeklődnek a sorozatok ilyen viselkedése iránt. Különösen érdekes az
yn+1=r⋅yn⋅(1-yn)(5)
összefüggéssel definiált sorozatok viselkedése: ezeknél végtelen sokszor tapasztalható újabb és újabb bifurkáció. Az (5) egyenlet pedig az
x=1001+KKy,r=1+K
az kapcsolatban van a mi nyulaink (3) egyenletével! A K=r-1 vezérlő paraméter K<2 értékére a sorozat konvergál. K1=2 és K2=6 közt bifurkál: nagy n-ekre a sorozat tagjai két érték közt ugrálnak (egyszeres periódusú csillapítatlan határciklus). K2=6 értéknél újabb bifurkáció történik (kétszeres periódusú határciklus: ugrálás 4 érték között), K3=2,564407...-nél újabb bifurkáció történik (három különböző frekvenciájú határciklus, ugrálás 8 érték között). K4=2,568799... felett 24 érték egyetlen határérték helyett, K5=2,569691... felett 25 érték, K6=2,569891... felett 26 érték stb. Ezen túl azt mondhatjuk, hogy Kr-1=K∞-A/δr és  Kr=K∞-A/δr+1 közt 2r érték közt ugrál a nyúllétszám (esetünkben A=2,6326... és δ=4,6692...). Végül K∞=2,569945651... fölött végtelen sok érték közt ugrál a létszám, végtelen sok periódus van jelen egyszerre, ami a periodicitás megszűnését jelenti. Ezt nevezik káosznak.
Akik nem olvasnak matematikai folyóiratokat, gyanútlanul számolnak kalkulátoraikkal. A K=3 vagy K=4 értéket választók győzelmét veszik biztosra. (Különösen akkor, ha megtanították őket az (1) egyenletet megoldó logisztikus görbére. Minél nagyobb a K annál meredekebben közelíti, annál hamarább belesímul a megoldás az x=100 határértékbe.) Mi azonban grafikusan is tájékozódhatunk a megoldásuk jellege felől!
Rajzoljuk fel az y=x+K100x(100-x) parabolát! A parabola az x=0 és az x=100(1+K-1) helyeken metszi az x-tengelyt, nyílása lefelé van, csúcsának koordinátái x=50(1+K-1) és y=25K-1(1+K)2. Húzzuk meg az y=x egyenest is! A két vonal az x=y=0 és az x=y=100 pontokban metszi egymást.
A populáció akkor állandó, ha xn+1=xn, azaz ha y=x. Ez megvalósulhat, ha x=0 (nincs nyúl) vagy ha x=100 (zérus növekedés a telítési értéken). Az üres sziget (x=0) instabil megoldás, már két nyúl betelepítése (x0=2) is rohamosan szaporodó népességhez vezet.

Legyen elsőként K=0,5. Jelöljük be az x0 pontot! Innen húzzunk függőlegest a parabolához, a metszéspont legyen P1. Ekkor P1 ordinátája x1. Húzzunk innen vízszintest az egyeneshez (Q1), ennek a pontnak az abszcisszája x1. Így ha ebből húzunk függőlegest a parabolához, megkapjuk az x2 ordinátájú P2 pontot. P2-ből menjünk vízszintesen az egyeneshez (Q2), e pont ordinátája x2, de a felette levő P3 parabolapont ordinátája már x3, és így tovább. A parabola és az egyenes közt függőleges-vízszintes cikk-cakkban haladva olyan pontsorozatot kapunk, melyek abszcisszaértékei az egymás után következő évek nyúllétszámát adják. K=0,5 esetén nyilvánvaló, hogy ez a létszám az x∞=100 értékhez konvergál, amint azt vártuk.
Ha ugyanezt a szerkesztést K=2 esetén is elvégezzük, akkor a Pn pontok már nem monoton konvergálnak az x=y=100 megoldáshoz, hanem túllőnek a célon. A túlszaporodást meredek visszaesés követi. A populáció oszcillálni kezd két stabil érték között. (A nyulaknál ez a jelenség kevésbé lép fel, de a földművelők jól ismerik a mezei pocokban vagy a cserebogárban gazdag és szegény évek változását.) A K≧2 körül fellépő jelenség neve: határciklus.
K≈3 esetén még drámaibb a populáció sorsa. A Pn pontok vadul ugrálnak fel és le. Az is előfordulhat, hogy x≦0 adódik (a populáció kihal). A matematikában ezt a jelenséget nevezik káosznak. (Az önmaguk táplálékát letaroló sáskajárások éhhalál-katasztrófáiról mindnyájan hallottunk.)
 

Tanulság. Végeredményben a K≦2 értéket választó diák nyer. K>2 értékre a numerikus számítás eredménye alapvetően különbözik a differenciálegyenlet-modell sima logisztikus görbéjétől. Mi lehet ennek az oka? Az (1) differenciálegyenletet
x(t+Δt)=x(t)+C⋅Δt⋅x(t)⋅100-x(t)100
alakba írva és a (3) iterációs képlettel összehasonlítva látható, hogy K=C⋅Δt. Ha Δt→0, ha tehát x(t) minden pillanatban reagál az élettér telítettségére, a dx/dt szaporodási sebességet az élettér pillanatnyilag érvényes (100-x)/100 telítettsége befolyásolja. Ilyen érzékeny (differenciált) módon simán elérhető a telítési érték.
Az állatok viszont véges Δt időközönként szaporodnak. Hogy a Δt időszak végén hány kölyök lesz, azt a Δt időszak elején levő létszám szabja meg. Ha K=C⋅Δt történetesen nagy szám (sáskák), akkor az xn értéket követő xn+1 egyedszám már túllő a célon, aminek a populáció kaotikus viselkedése lesz az eredménye.
Hasonló jelenség a matematikában és a természetben gyakran előfordul. A tanulságok innen is kézenfekvők:
 

a) Differenciálegyenlet (pl. a Newton-féle mozgásegyenlet) numerikus megoldásánál túlságosan nagy Δt lépések hamis eredményre vezethetnek.
b) Erős ütemű mozgás, szaporodás, fejlődés csak akkor engedhető meg (pl. populációdinamikában vagy közgazdaságtanban), ha a mindenkori hordozóképességet rövid időközönként, szinte pillanatról pillanatra érzékeljük, és reagálunk rá. Hosszú reakcióidő és durván nagy reakcióválasz káoszhoz vezethet.
c) Ha hosszú a Δt reakcióidőnk (pl. az autóvezető alkoholt fogyasztott), akkor egy közlekedési helyzetre olyan sokára fogunk reagálni, hogy az addigra egészen más lesz. Az eredmény: karambol. Ha valaki Δt-t nagyra választja, akkor C-nek kell kicsinek lennie, mert csak így biztosítható K=C⋅Δt<2. Autó helyett ajánlatosabb gyalog menni !
d) Az élet többi területére vonatkozó tanulságot mindenki maga fogalmazhatja meg.
 

Irodalom: Marx György-Tóth Eszter: Modellek a természettudományos nevelésben. Fizikai Szemle 31(1981)349. old.

Marx György: Simulation Games in Science Education, Europeanan Journal of Science Education (1983)

R. Hofstadter: Metamagical Themas. Scientific American 245(1981)

Nohum Joel, Párizs, szóbeli közlés.
*Ezzel a sorozattal foglalkozott a P. 270. Probléma, KÖMAL, 57. kötet (1978), 153-155. oldal, 59. kötet (1979), 205-216. oldal.-Szerk.