| Cím: | Szabályos toroidok | ||
| Szerző(k): | Szilassi Lajos | ||
| Füzet: | 1983/november, 97 - 104. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Szakmai cikkek | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Szabályos toroidok Mint ismeretes, a szabályos poliéderek minden csúcsába ugyanannyi él fut be, és minden lapjának ugyanannyi éle van. Egy poliéder topológiailag szabályos, ha a fenti kikötéseket nem szigorítjuk további (pl. az élek és lapok szögeire vonatkozó) kikötéssel. Ebben a cikkben ilyen poliéderekkel fogunk megismerkedni, előbb azonban áttekintünk néhány, a poliéderekkel kapcsolatos fogalmat és egyszerűbb összefüggést. Egy poliéder közönséges, ha a poliédertest bármely két pontja összeköthető olyan töröttvonallal, amely nem metszi a poliéder felületét, továbbá minden csúcsánál a csúcsot tartalmazó lapok egy ciklust alkotnak úgy, hogy a ciklus szomszédos tagjai a szomszédos ‐ közös éllel rendelkező ‐ lapok. A közönséges poliéder minden éle pontosan két lap határán van. Egy poliéder egyszerű, ha közönséges, topológiailag gömbszerű, azaz folytonos deformálással gömbbé alakítható, lapjai pedig egyszerű sokszögek. Pl. a konvex poliéderek egyszerűek, de nem kell minden egyszerű poliédernek feltétlenül konvexnek lennie. Az egyszerű poliéderek körében érvényes az Euler‐féle
Az összefüggés alkalmazásával könnyen belátható, hogy csak öt "topológiailag'' szabályos, egyszerű poliéder létezik, és ezek mindegyike realizálható úgy, hogy lapjai és testszögletei szabályosak és egybevágók legyenek. Így jutunk az ismert öt szabályos egyszerű poliéderhez. Nevezzük toroidnak a topológiailag tórusszerű, azaz folytonos deformálással tórusszá (körgyűrű‐felületté) alakítható, egyszerű sokszögekkel határolt közönséges poliédereket. Az így értelmezett toroidokra az Euler‐féle összefüggés így módosul:
Egy ‐ a szűkebb értelemben vett ‐ toroidot nevezzünk szabályosnak, ha minden csúcsába ugyanannyi él fut be, és minden lapjának ugyanannyi éle van. A toroidokat vizsgálva nem reménykedhetünk abban, hogy a lapok, ill. testszögletek mind szabályosak és egybevágók lesznek, így a "szabályos'' jelző itt nyilvánvalóan topológiai tulajdonság. Ismerkedjünk meg a szabályos toroidok néhány érdekes képviselőjével! 1. Legyen egy szabályos toroid minden lapjának éle, és minden csúcsába fusson be él. Az és szorzatok egyaránt az élek számának a kétszeresét adják, mivel minden él pontosan két lapra és két csúcsra illeszkedik. Ezek, valamint a toroidokra érvényes Euler‐féle (2) összefüggés alapján kapjuk, hogy osztály: , ; osztály: , ; osztály: , . Mint ismeretes, a síkot egybevágó szabályos sokszögekkel hézagmentesen csak három módon lehet lefedni: a szabályos háromszögekkel, négyzetekkel és a szabályos hatszögekkel. (Minden élnek pontosan két lap határán kell lennie. Ezt a kikötést elmulasztva a háromszögekkel és a négyzetekkel való lefedés nem egyértelmű.) A három parkettázás topológiailag éppen az előző három esetnek felel meg. Ha egy ilyen kiparkettázott síkból kiragadunk egy "elég nagy'' téglalapot, és összeragasztjuk a szemben levő éleit, akkor egy olyan tóruszra rajzolt térképhez jutunk, amely topológiailag szabályos. (Valóban: egy téglalap két szemben levő élét összeragasztva egy hengerpalástot kapunk, ebből pedig a másik két ‐ most már kör alakú ‐ él összeragasztásával tóruszt.) Ha az így kapott tóruszra rajzolt szabályos térképnek elég sok tartománya van, akkor a síklapokkal való realizálásnak nincs elvi akadálya. Mondhatjuk tehát, hogy mindhárom osztályba végtelen sok szabályos toroid tartozik. Érdekes kérdés azonban, hogy legkevesebb hány lapra, ill. csúcsra van szükség az egyes osztályokba tartozó szabályos toroidok előállításához, esetleg szigorítva a kikötést azzal, hogy a toroid lapjai ‐ vagy testszögletei ‐ az egybevágóság szempontjából minél kevesebb osztályt alkossanak. 2. Az osztályba tartozó minimális lap- (és csúcs-) számú szabályos toroid a KÖMAL 1982. novemberi számában bemutatott, átló nélküli ‐ ún. Császár‐féle ‐ poliéder. (KÖMAL 1982. 65. kötet, 3‐4. szám, 154‐155. oldal.) Valóban, egy osztálybeli szabályos toroidnak minden csúcsába hat él fut be, így legalább hét csúcsa van. Ez pedig éppen egy hét csúcsú toroid. (Belátható, hogy hétnél kevesebb csúcsú toroid egyáltalán nem létezhet.) Az említett cikkben közölt adatok alapján épített toroid (nevezzük ezt -nek) ‐ mint a szerző is említi ‐ eléggé "zsúfoltnak'' tűnik. Van olyan lapszöge is, amely több, mint -os. Egy "szellősebb'' változat kereséséhez olyan számítógépi programot készítettünk, amely a hét csúcs derékszögű koordinátáiból kiindulva először ellenőrzi, hogy a hét pont által meghatározott poliéder nem önátmetsző-e, majd kiszámítja a poliéder éleinek hosszát, élszögeit és lapszögeit. Az 1. táblázatban a poliéder három változatának az adatait közöljük. A poliéder adatai alig különböznek az eredeti ‐ Császár Ákos által közölt ‐ adatoktól. A táblázatban ‐ a könnyebb áttekinthetőség érdekében ‐ számokkal jelöltük a csúcsokat. A poliédert alkotó háromszög‐lapokat így számhármasok jelzik. A poliéder egyértelmű megadásához nem elég megadnunk a hét csúcs koordinátáit, azt is tudnunk kell, hogy a hét pont által meghatározott háromszög közül melyik az a 14, amely a poliéder felületét alkotja. Megfigyelhetjük, hogy mindhárom változatban az 1. és 6., 2. és 5., valamint a 3. és 4. csúcs egymásnak a koordináta‐rendszer tengelyére vonatkozó tükörképei, így a táblázatban egymás alá írt lappárok egybevágóak. Ugyancsak egybevágók az előbbi csúcspárokhoz tartozó testszögletek is. Így az egybevágóság szempontjából mindhárom változat lapjai hét, testszögletei négy osztályba sorolhatók. Az 1. táblázat adatait vizsgálva kitűnik, hogy -nek és -nek ugyanott vannak konkáv lapszögei. A csúcsok folytonos mozgatásával a két változat átvihető egymásba úgy, hogy eközben soha ne legyen önátmetsző a poliéder felülete. A változathoz a csúcsok alapos átrendezésével jutottunk, így ez csak topológiai tulajdonságaiban egyezik meg az előzőkkel. 1. táblázat A poliéder lapjai: (1-6-2) (1-4-2) (2-4-5) (1-3-4) (1-5-7) (5-4-7) (4-6-7) (6-1-5) (6-3-5) (5-3-2) (6-4-3) (6-2-7) (2-3-7) (3-1-7) A 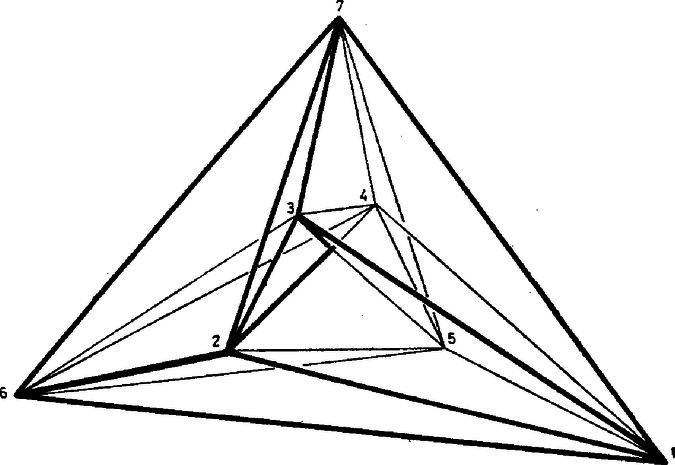 1. ábra Felvethető a kérdés, hogy a koordináták változtatásával vagy átrendezésével kaphatunk-e ezeknél lényegesen " szellősebb'', átló nélküli toroidot. 3. A szabályos toroidok Vegyünk egy (pl. szabályos) 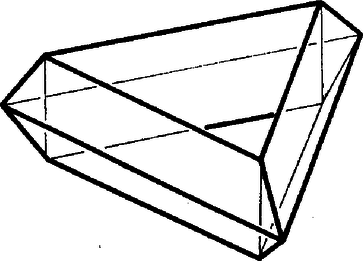 2. ábra Az előbbi eljárással 4. Mint láttuk, a Császár‐poliéder legfontosabb tulajdonsága, hogy bármely két csúcsát él köti össze. Ezzel a poliéderrel igen szoros, ún. duális kapcsolatban van az 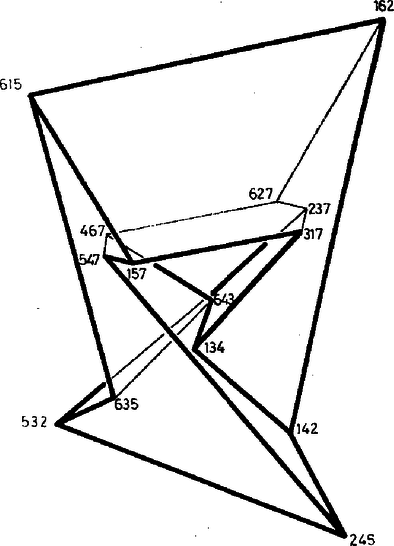 3. ábra 2. táblázat 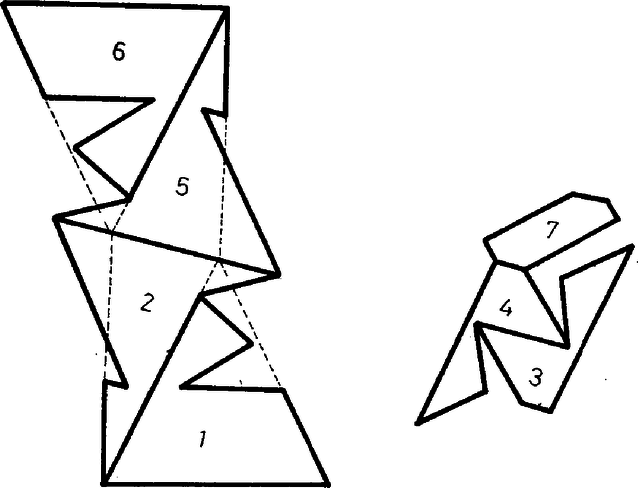 4. ábra Belátható, hogy hétnél kevesebb lapsíkkal egyáltalán nem állítható elő toroid, így ez a poliéder nemcsak az 5. A múlt században felvetődött térképszínezési problémák (pl. a négy‐színprobléma) közül Heawood 1890-ben igazolta, hogy a tóruszra rajzolt bármely térkép kiszínezéséhez elegendő hét szín. Ugyanekkor azt is megmutatta, hogy a hét szín szükséges is. Ugyanis rajzolt a tóruszra olyan hét tartományból álló térképet, amelynek bármely két tartománya szomszédos, így a helyes kiszínezéséhez minden tartományt különböző színűre kell festenünk. Az itt megismert poliéderrel ezt a Heawood‐féle hétszínű térképet állítottuk elő, hét egyszerű síkbeli hatszögből. A Heawood‐féle hétszínű térkép realizálható olyan toroiddal is, melynek minden lapja szabályos sokszög. (Persze akkor a tartományok már nem egyetlen lapból állnak.) Ennek a ‐ B. M. Stewart-tól származó ‐ konstrukciónak a hálózatát, valamint külön‐külön a toroid "belső'' és "külső'' felét az 5. ábrán láthatjuk. A sokszögekre írt számok egy‐egy színt jelölnek. Az ábrát vagy az ez alapján készített modellt vizsgálva meggyőződhetünk, hogy valóban minden szín szomszédos minden színnel. 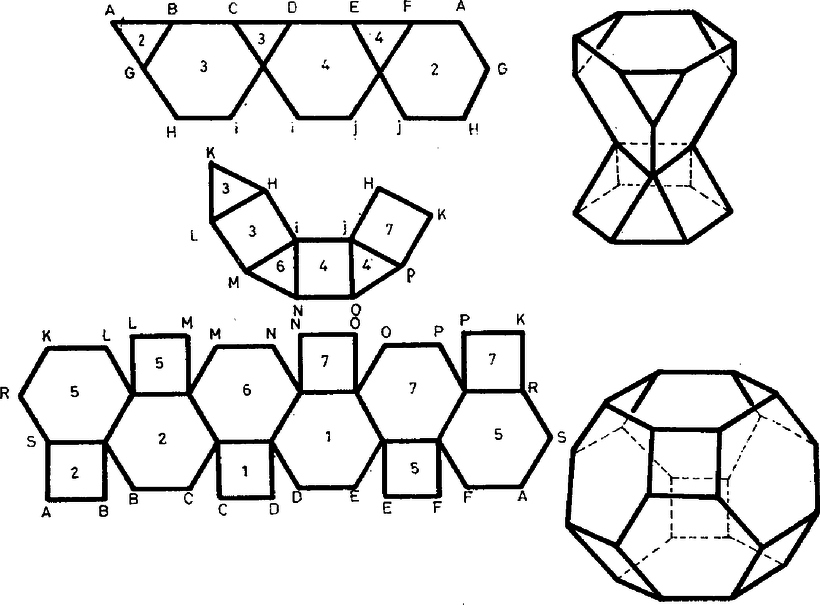 5. ábra Előállításához tekintsük az 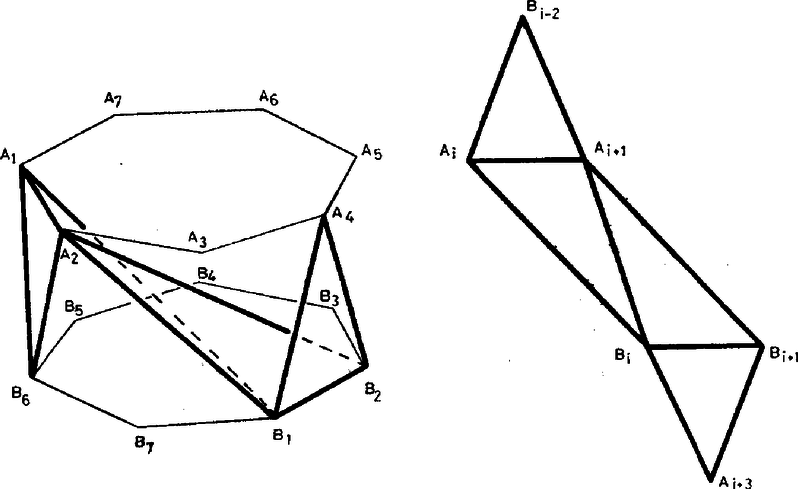 6. ábra A poliéder előállításához tetszőlegesen megadhatjuk a két szabályos hétszög síkjának a távolságát, vagy pl. az egyenlő szárú Ez a poliéder az Ennél kevesebb lap- és csúcsszámú, ugyanilyen (egybevágó testszögletű és kétféle lapból felépített) Vajon legkevesebb hány lapra van szükségünk ahhoz, hogy csupa egybevágó lapokból építhessünk toroidot? Ugyancsak B. M. Stewart konstruált olyan 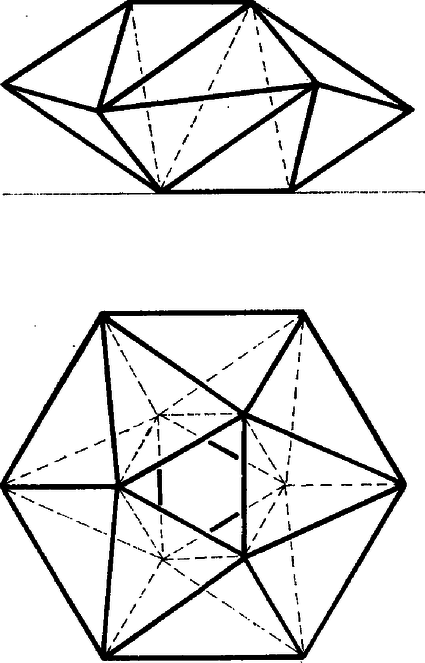 7. ábra Szilassi Lajos, Szeged |