Kezdőlap


Cím:	1982. évi Kürschák József matematikai tanulóverseny feladatainak megoldása
Szerző(k):	Surányi János
Füzet:	1983/február, 50 - 60. oldal	PDF \| MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1982. évi Kürschák József Matematikai Tanulóverseny

feladatainak megoldása

1. Adott a térben egy egész oldalhosszúságú kocka, amelyről tudjuk, hogy az egyik lapján levő négy csúcs koordinátái valamennyien egész számok. Bizonyítandó, hogy a másik négy csúcs koordinátái is egész számok.

Megoldás. Fel fogjuk használni ‐ amit a megjegyzések keretében be is bizonyítunk ‐, hogy az r(

r_{1}

r_{2}

r_{3}

) és az u(

u_{1}

u_{2}

u_{3}

) koordinátáival adott két vektor akkor és csak akkor merőleges, ha

\begin{matrix} r_{1} u_{1} + r_{2} u_{2} + r_{3} u_{3} = 0. \end{matrix}

Legyenek egy

A B C D E F G H

kocka egy lapjának

A

B

C

D

csúcsai egész koordinátájúak, a kocka élének hossza a szintén egész szám, az

A

-val szomszédos harmadik csúcs

E

. Azt kell belátnunk, hogy

E

F

G

H

is egész koordinátájú. Elég belátnunk, hogy pl. az

\vec{A E}

vektor koordinátái egész számok, hiszen

E

F

G

H

koordinátáit úgy kaphatjuk, hogy

A

B

C

, ill.

D

koordinátáihoz hozzáadjuk

\vec{A E}

koordinátáit.

Legyenek az

\vec{A B} = b

\vec{A D} = d

\vec{A E} = e

koordinátái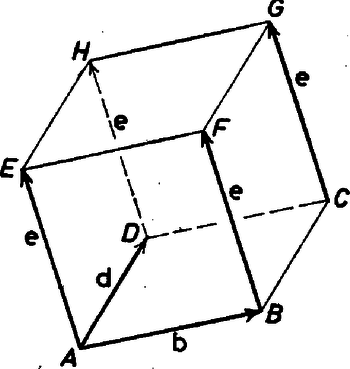

\begin{matrix} (b_{1}, b_{2}, b_{3}), (d_{1}, d_{2}, d_{3}), ill (e_{1}, e_{2}, e_{3}) . \end{matrix}

Ezeket úgy kaphatjuk, hogy a

B

D

, ill.

E

pont koordinátáiból kivonjuk

A

koordinátáit. A b és d vektor koordinátái tehát egész számok, és azt kell belátnunk, hogy e koordinátái is azok. A b és d vektorok hossza

a

, és a vektorok merőlegesek, tehát koordinátáikra teljesül, hogy

\begin{matrix} (1) b_{1}^{2} + b_{2}^{2} + b_{3}^{2} = a^{2}, (2) d_{1}^{2} + d_{2}^{2} + d_{2}^{3} = a^{2}, (3) b_{1} d_{1} + b_{2} d_{2} + b_{3} d_{3} = 0. \end{matrix}

Az e vektor merőleges b-re is, d-re is és

a

hosszúságú, tehát

\begin{matrix} b_{1} e_{1} + b_{2} e_{2} + b_{3} e_{3} = 0, \\ e_{1}^{2} + e_{2}^{2} + e_{3}^{2} = a^{2} . \\ d_{1} e_{1} + d_{2} e_{2} + d_{3} e_{3} = 0, \end{matrix}

Az első két egyenletből kifejezhetjük

e_{1}

e_{2}

e_{3}

-at, de ezt a 3 adatot a két egyenlet csak egy

k

közös szorzó tényező erejéig határozza meg.A számításokat elvégezve azt kapjuk, hogy

\begin{matrix} e_{1} = k (b_{2} d_{3} - b_{3} d_{2}), e_{2} = k (b_{3} d_{1} - b_{1} d_{3}), e_{3} k (b_{1} d_{2} - b_{2} d_{1}) . \end{matrix}

A vektor hosszát kiszámítva

\begin{matrix} a^{2} = k^{2} {b_{2}^{2} d_{3}^{2} + b_{3}^{2} d_{2}^{2} + b_{3}^{2} d_{1}^{2} + b_{1}^{2} d_{3}^{2} + b_{1}^{2} d_{2}^{2} + b_{2}^{2} d_{1}^{2} - 2 b_{2} d_{2} b_{3} d_{3} - 2 b_{1} d_{1} b_{3} d_{3} - 2 b_{1} d_{1} b_{2} d_{2}} . \end{matrix}

(4)

Bontsuk a kivonandókat 2‐2 egyenlő tag összegére és a másik két tag egyikének, ill. másikának egyik részével közös tényezőket emeljük ki. Ekkor a kivonandó így alakul

\begin{matrix} - b_{2} d_{2} b_{3} d_{3} - b_{3} d_{3} b_{1} d_{1} - b_{2} d_{2} b_{3} d_{3} - b_{2} d_{2} b_{1} d_{1} - b_{1} d_{1} b_{2} d_{2} - b_{1} d_{1} b_{3} d_{3} = \\ = - b_{3} d_{3} (b_{1} d_{1} + b_{2} d_{2}) - b_{2} d_{2} (b_{3} d_{3} + b_{1} d_{1}) - b_{1} d_{1} (b_{2} d_{2} + b_{3} d_{3}) = \\ = - b_{3} d_{3} (- b_{3} d_{3}) - b_{2} d_{2} (- b_{2} d_{2}) - b_{1} d_{1} (- b_{1} d_{1}) . \end{matrix}

Az utolsó lépésben mindhárom tag második tényezőjére a (3) összefüggést alkalmaztuk. Eredményünket (4)-be beírva azt kapjuk, hogy

\begin{matrix} a^{2} = k^{2} {b_{2}^{2} d_{3}^{2} + b_{3}^{2} d_{2}^{2} + b_{3}^{2} d_{1}^{2} + b_{1}^{2} d_{3}^{2} + b_{1}^{2} d_{2}^{2} + b_{2}^{2} d_{1}^{2} + b_{3}^{2} d_{3}^{2} + b_{2}^{2} d_{2}^{2} + b_{1}^{2} d_{1}^{2}} = \\ = k^{2} {(b_{1}^{2} + b_{2}^{2} + b_{3}^{2}) (d_{1}^{2} + d_{2}^{2} + d_{3}^{2})} = k^{2} a^{4}, k^{2} = \frac{1}{a^{2}} . \end{matrix}

Az e vektor koordinátái tehát:

\begin{matrix} \frac{b_{2} d_{3} - b_{3} d_{2}}{a}, \frac{b_{3} d_{1} - b_{1} d_{3}}{a}, \frac{b_{1} d_{2} - b_{2} d_{1}}{a}, \end{matrix}

vagy ezek ellentettjei. Világos, hogy ezek racionális számok, azt kell belátnunk, hogy egészek.
Elég ezt a fenti hármasról belátni, mert egész szám ellentettje is egész. Elég továbbá egyik koordinátáról belátni, hogy az egész, mert akkor az indexek alkalmas cseréjével adódik a másik kettő egész voltának a bizonyítása.
Azt fogjuk belátni, hogy a koordináta négyzete egész szám. Tudjuk, hogy ha egy racionális szám négyzete egész szám, akkor az alap is egész szám. Az első koordináta számlálójának négyzetét fogjuk átalakítani:

\begin{matrix} {(b_{2} d_{3} - b_{3} d_{2})}^{2} = b_{2}^{2} d_{3}^{2} + b_{3}^{2} d_{2}^{2} - 2 b_{2} d_{2} b_{3} d_{3} = \\ = b_{2}^{2} d_{3}^{2} + b_{3}^{2} d_{2}^{2} - b_{2} d_{2} (- b_{1} d_{1} - b_{2} d_{2}) - b_{3} d_{3} (- b_{3} d_{3} - b_{1} d_{1}) = \\ = b_{2}^{2} d_{3}^{2} + b_{3}^{2} d_{2}^{2} + b_{1} d_{1} b_{2} d_{2} + b_{2}^{2} d_{2}^{2} + b_{3}^{2} d_{3}^{2} + b_{1} d_{1} b_{3} d_{3} = \\ = b_{2}^{2} d_{3}^{2} + b_{3}^{2} d_{2}^{2} + b_{2}^{2} d_{2}^{2} + b_{3}^{2} d_{3}^{2} + b_{1} d_{1} (b_{2} d_{2} + b_{3} d_{3}) = \\ = (b_{2}^{2} + b_{3}^{2}) (d_{2}^{2} + d_{3}^{2}) - b_{1}^{2} d_{1}^{2} = (a^{2} - b_{1}^{2}) (a^{2} - d_{1}^{2}) - b_{1}^{2} d_{1}^{2} = a^{2} (a^{2} - b_{1}^{2} - d_{1}^{2}) . \end{matrix}

Itt ismét két tagra bontottuk a kivonandót és egyszer az első, másszor a második két tényező szorzatát helyettesítettük a (3) összefüggésből adódó értékével, majd alkalmaztuk (1)-et, (2)-t és mégegyszer (3)-at.
Azt nyertük tehát, hogy

\begin{matrix} {(\frac{b_{2} d_{3} - b_{3} d_{2}}{a})}^{2} \end{matrix}

egész szám, és ebből ‐ mint már említettük ‐ következik az alap egész volta is. Ezzel a feladat állítását bizonyítottuk.

Megjegyzések. 1. A megoldás elején kimondott állítás így látható be: Az, hogy

r

és

u

merőleges egymásra, azt jelenti, hogy az

O R U

háromszög derékszögű (a 2. ábra betűzését használjuk), ez pedig egyenértékű állítás azzal, hogy a háromszög oldalaira teljesül Pitagorász tétele. Az r‐ u vektor koordinátái (

r_{1} - u_{1}

r_{2} - u_{2}

r_{3} - u_{3}

), így a feltételt koordinátákkal felírva

\begin{matrix} r_{1}^{2} + r_{2}^{2} + r_{3}^{2} + u_{1}^{2} + u_{2}^{2} + u_{3}^{2} = {(r_{1} - u_{1})}^{2} + {(r_{2} - u_{2})}^{2} + {(r_{3} - u_{3})}^{2} = \\ = r_{1}^{2} + r_{2}^{2} + r_{3}^{2} + u_{1}^{2} + u_{2}^{2} + u_{3}^{2} - 2 (r_{1} u_{1} + r_{2} u_{2} + r_{3} u_{3}) . \end{matrix}

Ez pedig valóban egyenértékű azzal, hogy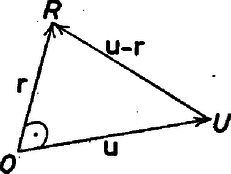

\begin{matrix} r_{1} u_{1} + r_{2} u_{2} + r_{3} u_{3} = 0. \end{matrix}

2. Aki ismeri a vektorok skaláris szorzatát, annak a most levezetett összefüggés jól ismert, aki pedig a vektoriális szorzatot is ismeri, az tudja, hogy az e vektor koordinátáiban

k

szorzói a vektorszorzat koordinátái, és azt is, hogy merőleges vektorok vektorszorzatának a hossza a tényezők hosszának a szorzata, esetünkben tehát

a^{2}

. Így

k

vagy

\frac{1}{a}

vagy

- \frac{1}{a}

. Ezeket felhasználva lényegesen lerövidül a megoldás.

3. A bizonyítás végén felhasznált tétel: ha egy racionális szám négyzete egész, akkor az alap is egész, a számelmélet alaptételének a következménye. E tétel szerint az egész számok törzstényezőkre bontott alakjában a tényezők sorrendtől eltekintve egyértelműen vannak meghatározva.
Valóban, ha egy

v / w

tört (

v, w

egész) nem egész szám, akkor

w

-nek van olyan

p

törzstényezője, ami

v

felbontásában kisebb hatványon szerepel, mint

w

-ében (esetleg egyáltalán nem szerepel). De

\begin{matrix} {(\frac{v}{w})}^{2} = \frac{v^{2}}{w^{2}} . \end{matrix}

Az alaptétel szerint

v^{2}

-nek és

w^{2}

-nek nincs más prímtényezős felbontása, mint amelyik a

v

, ill.

w

felbontásában szereplő prímek hatványkitevőinek kétszerezésével keletkezik. Ekkor azonban

p

v^{2} / w^{2}

tört nevezőjében is magasabb hatványon szerepel, mint, a számlálóban, tehát ez a tört sem lehet egész szám.

2. Bizonyítsuk be, hogy minden

k > 2

egész számhoz létezik végtelen sok olyan

n

természetes szám, hogy az

n

n + 1

...

n + k - 1

számok legkisebb közös többszöröse nagyobb, mint az

n + 1

n + 2

...

n + k

számok legkisebb közös többszöröse.

(A legkisebb közös többszörös annyiszor fordul elő az alábbi szövegben, hogy röviden lkkt-t írunk helyette.)

I. megoldás. Az

a_{1}

a_{2}

...

a_{m}

számok lkkt-ét ‐ amit így szokás jelölni: [

a_{1}, a_{2}, ..., a_{m}

], ‐ úgy határozhatjuk meg, hogy minden prímszámot, amelyik a számok valamelyikének osztója, vesszük azon a legmagasabb hatványon, amelyiken osztója valamelyik

a_{i}

-nek, és ezeket a prímszámhatványokat összeszorozzuk. Eszerint

\begin{matrix} T_{n} = [n, n + 1, ..., n + k - 1] és T_{n + 1} = [n + 1, n + 2, ..., n + k - 1, n + k] \end{matrix}

prímhatványokra történő felbontásában egyenlő hatványon szerepelnek azok a prímszámok, amelyeknek a legmagasabb hatványa az

n + 1

n + 2

...

n + k - 1

számok valamelyikének a felbontásában fordul elő.

T_{n}

-ben magasabb hatványon szerepelnek, mint

T_{n + 1}

-ben azok a prímek (ha vannak), amelyeknek magasabb hatványa osztója

n

-nek, mint

n + 1

...

n + k

bármelyikének, és alacsonyabb hatványon azok az esetleges prímek, amelyeknek magasabb hatványa osztója

n + k

-nak, mint

n

...

n + k - 1

bármelyikének.
Legyenek

p_{1}

...

p_{g}

az előbbi tulajdonságú prímek és legyen

p_{j}

T_{n}

-nek (s így

n

-nek is) a

t_{j}

-edik hatványon osztója,

T_{n + 1}

-nek az

u_{j}

-edik hatványon osztója, ahol

t_{j} > u_{j}

(

j = 1, ..., g

); hasonlóan legyenek az utóbbi tulajdonsággal rendelkező prímek

q_{1}

...

q_{h}

és

q_{j}

T_{n}

-nek

v_{j}

-edik,

T_{n + 1}

-nek

w_{j}

-edik hatványon osztója,

v < w_{j} (j = 1, ..., h)

. Ekkor

\begin{matrix} T_{n + 1} = \frac{q_{1}^{w_{1} - v_{1}} ... q_{h}^{w_{h} - v_{h}}}{p_{1}^{t_{1} - u_{1}} ... p_{g}^{t_{g} - u_{g}}} T_{n} . \end{matrix}

(1)

Végtelen sok olyan

n

értékre van tehát szükségünk, amelyekre a

T_{n}

a jobb oldalon 1-nél kisebb számmal van megszorozva. Ehhez legegyszerűbb

n

-et úgy választani, hogy

n + 1

...

n + k - 1

egyikével se legyen 1-nél nagyobb közös osztója,

(n + k)

-nak viszont legalább az egyikükkel legyen. Ekkor a tört nevezője

n

lesz, a számlálója pedig legfeljebb

\frac{n + k}{2}

. A tört tehát nem nagyobb, mint

\frac{n + k}{2 n}

; ez pedig 1-nél kisebb, ha

n

nagyobb

k

-nál.

Ha végtelen sok

n

-re kielégítjük az első két feltételt, akkor közülük végtelen sok nagyobb is lesz mint

k

, tehát elég olyan

n

egészeket keresnünk, amelyekre

n

relatív prím az

n + 1

...

n + k - 1

számokhoz,

n + k

pedig legalább egyikhez nem relatív prím. A feladatot megoldó versenyzők mind ezt az utat választották, de az

n

kívánt tulajdonságait igen különböző, módokon biztosították. Bemutatjuk a lényegében legegyszerűbbnek látszót.
Ha valamilyen

j

-re

n

-nek és

(n + j)

-nek van 1-nél nagyobb közös osztója, akkor ez közös osztója

n

és

(n + j) - n = j

-nek is és megfordítva is:

n

és

j

közös osztói

(n + j)

-nek is osztói. Azt kell tehát elérnünk, hogy kiválasztandó számaink az

\begin{matrix} 1, 2, ..., k - 1 \end{matrix}

(*)

számokhoz relatív prímek legyenek, tehát például a szorzatukhoz is. Ezzel a tulajdonsággal rendelkeznek az^{$^{*}$}

\begin{matrix} 1 \cdot 2 \cdot ... \cdot (k - 1) \end{matrix}

szorzat többszöröseinek a szomszédai, tehát a

c ((k - 1)!) \pm 1

számok.

Ahhoz, hogy a

k

-val nagyobb

c ((k - 1)!) + k \pm 1

a (*) alatti számok valamelyikéhez ne legyen relatív prím, a kettős előjelből a negatívat célszerű választani. Ez esetben a

k

-val növelt szám osztható (

k - 1

)-gyel, és az (

n + 1

)-ként adódó

c ((k - 1)!)

is osztható (

k - 1

)-gyel.
Ha tehát az

\begin{matrix} n_{c} = c ((k - 1)!) - 1 \end{matrix}

számokat választjuk, az (1) egyenlőség nevezője

n_{c}

lesz, számlálója pedig legfeljebb

\begin{matrix} \frac{n_{c} + k}{k - 1} . \end{matrix}

Így

\begin{matrix} T_{n_{c} + 1} \leq \frac{n_{c} + k}{(k - 1) n_{c}} T_{n_{c}} . \end{matrix}

Itt

k - 1 \geq 2

, mert a feladat feltétele szerint

k > 2

. Ha tehát

n_{c} > k

is teljesül (ami

k = 3

-nál

c \geq 3

-ra,

k > 3

esetén minden pozitív egész

c

-re igaz), akkor

\begin{matrix} \frac{n_{c} + k}{(k - 1) n_{c}} < 1, tehát T_{n_{c} + 1} < T_{n_{c}} . \end{matrix}

Ezzel a feladat állítását igazoltuk.

Megjegyezzük, hogy

k = 2

-re nem igaz a feladat állítása,

[n, n + 1] = n (n + 1)

és ez növekvő

n

-nel állandóan növekszik.

Megjegyzések. 1. A lkkt-nek a megoldás elején ismertetett megadásmódja ismét az első feladathoz fűzött 3. megjegyzésben említett számelmélet alaptételéből következik.

2. Egy versenyző

(k - 1)

! helyett a lényegesen kisebb

[1, 2, ..., k - 1]

számot használta, de elég lett volna ehelyett a

k

-nál kisebb prímek szorzatát venni, amint azt könnyen beláthatja az olvasó. Összehasonlításul már

k = 21

-re

(k - 1)

! felette van a 4700 billiónak,

[1, 2, ..., k - 1]

közel

233, 3

millió, a prímek szorzata pedig valamivel

9, 7

millió alatt van.

II. Megoldás. Megkaphatjuk az

[n, n + 1, ..., n + k - 1]

lkkt-t úgy is, hogy az

n (n + 1) ... (n + k - 1)

szorzatot elosztjuk bizonyos számokkal, tehát

\begin{matrix} [n, n + k, ..., n + k - 1] = \frac{n (n + 1) ... (n + k - 1)}{v_{n, k}} \end{matrix}

(2)

alakban, ahol

v_{n, k}

természetes szám.
Mielőtt ennek helyességét belátnánk, nézzük meg, hogyan alakul ennek felhasználásával a feladat állításában szereplő egyenlőtlenség. A megfelelő kifejezéseket beírva, kézenfekvő átalakításokkal az

\begin{matrix} n v_{n + 1, k} > (n + k) v_{n, k} \end{matrix}

vagy

\begin{matrix} n (v_{n + 1, k} - v_{n, k}) > k v_{n, k} \end{matrix}

(3)

adódik. A bal oldalnak pozitívnak kell lennie, amihez

\begin{matrix} v_{n + 1, k} > v_{n, k} \end{matrix}

(4)

szükséges. Ha ez fennáll, akkor az utolsó egyenlőtlenség bizonyosan teljesül, ha maga

n

nagyobb a jobb oldalnál, mert a szorzója legalább 1.

Ezek alapján a feladat állítása következik abból, ha megmutatjuk, hogy

a) Minden adott

k

-ra

v_{n, k}

egy csak

k

-tól függő korlátnál nem nagyobb, és
b) ha

k \geq 3

, adott, akkor

v_{n, k}

értéke végtelen sokszor változik.

Valóban a b) szerinti változás nem lehet valamilyen határon túl mindig csökkenés, hiszen

v_{n, k}

-nak mindig pozitív egésznek kell lennie, de nem lehet valamilyen értéken túl mindig növekedés sem, hiszen akkor

v_{n, k}

minden korláton túlnőne, ami a) miatt nem lehet. Van tehát végtelen sok olyan

n

, amelyre (4) teljesül.
Legyen

V

egy olyan érték, aminél

v_{n, k}

sohasem nagyobb, akkor mindazokra az

n

-ekre, amikre (4) teljesül és amelyek

k V

-nél nagyobbak, igaz, hogy

\begin{matrix} n (v_{n + k - 1} - v_{n, k}) > k V \geq k v_{n, k}, \end{matrix}

tehát teljesül (3), abból pedig a feladat állításában szereplő egyenlőtlenség ekvivalens átalakításokkal következik.
A feladat állításának bizonyításához tehát elég a (2) alakú előállítás létezését bizonyítani (egész nevezővel) és a nevező a) és b) tulajdonságát.
A (2) felbontáshoz eljuthatunk úgy, hogy leírjuk egyenként a számláló tényezőit és

n + j

leírása után

(1 \leq j \leq k - 1)

nézzük annak prímszámhatványok szorzatára bontott alakját. Ha van a prím alapok közül valamelyiknek korábban is többszöröse, akkor veszünk egy olyan

n + i (0 \leq i < j)

tényezőt, amelyik az illető prím legnagyobb hatványával osztható, és ha ez a hatvány nem nagyobb az

(n + j)

-ben szereplő hatványnál, akkor a nevezőbe írjuk, különben az

(n + j)

-ben fellépő hatványt írjuk a nevezőbe. Világos, hogy így a

k

-adik lépésben megkapjuk a keresett lkkt-t.

v_{n, k}

a nevezőbe került prímhatványok szorzata.
A nevezőbe írt prímszámhatvány osztója

(n + i)

-nek is,

(n + j)

-nek is, tehát a különbségüknek

j - i

-nek is, ami pozitív és nem nagyobb

j

-nél. Az

n + j

sorravételénél tehát a

j

j - 1

...

, 2 bizonyos prímszámhatvány osztóival osztunk, tehát összességében nem nagyobb számmal, mint

j

! Ezt

j = 1, 2, ..., (k - 1)

-re alkalmazva kapjuk, hogy

\begin{matrix} v_{n, k} \leq 2! 3! ... (k - 1)!, \end{matrix}

v_{n, k}

csak véges sok értéket vesz fel.^{$^{*}$} Ezzel beláttuk a (2) alakú felbontás létezését és az a) állítást. Igazoljuk még b)-t.
Világos, hogy

v_{n,2} = 1

minden

n

-re.
Legyen

p

egy

k

-nál kisebb prímszám, amelyik nem osztója

k

-nak. ‐ Ilyenek pl. a

k - 1 (\geq 2)

prímosztói. ‐ Válasszuk

n

-et úgy, hogy

n + k

többszöröse legyen

p

-nek, és vizsgáljuk

p

kitevőjét

v_{n, k}

és

v_{n + 1, k}

prímhatványok szorzatára bontott alakjában.
Nem lehet

n

is többszöröse

p

-nek, mert különben az

(n + k) - n = k

is osztható volna

p

-vel, ellentétben

p

választásával.
Mivel

p < k

, van többszöröse az

n + 1

n + 2

...

n + k - 1

számok közt. Ha áttérünk

[n, n + 1, ..., n + k - 1]

-ről

[n + 1, ..., n + k - 1, n + k]

-ra, akkor a (2) jobb oldalának számlálójából elmarad a

p

-vel nem osztható

n

tényező és megjelenik a

p

-vel osztható

n + k

. Világos, hogy

n

elhagyása a

p

kitevőjét nem befolyásolja, viszont

n + k

hozzávétele után az előállításra vonatkozó gondolatmenetet követve látható, hogy a nevezőbe kell írnunk

p

-nek valamilyen hatványát.

v_{n + 1, k}

tehát

p

-nek magasabb hatványával osztható, mint

v_{n, k}

, s így (függetlenül esetleges egyéb különbségektől) különböző számok, mivel a számok prímhatványokra történő felbontása lényegében egyértelmű.

Megjegyzések. 1. Az I. megoldás során több módon is megadtunk adott

k

-hoz végtelen sok olyan

n

értéket, amire teljesül a

T_{n} < T_{n + 1}

egyenlőtlenség, de távolról sem adtuk meg az összes ilyen

n

-et. Ez reménytelenül nehéz feladatnak is látszik. ^{$^{*}$} Belátható, hogy a legkisebb

n

is, ami ott adódik, sokkal nagyobb

k

-nál.
Jelöljük

n_{k}

-val adott

k

-hoz a legkisebb olyan

n

-et, amire teljesül a

T_{n} < T_{n + 1}

egyenlőtlenség. Néhány értéket a következő táblázat mutat:

\begin{matrix} k & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 & 29 & 30 & 31 & 32 & 210 \\ n_{k} & - & 5 & 5 & 7 & 9 & 8 & 11 & 11 & 11 & 13 & 13 & 17 & 16 & 17 & 17 & 31 & 47 & 32 & 37 & 237 \end{matrix}

Láthatólag ezek az értékek alig nagyobbak

k

-nál. Az világos, hogy

n_{k}

-nak

k

-nál nagyobbnak kell lennie, mert ha

n \leq k

, akkor az

n + 1, ..., n + k

között van

n

-nel osztható, hiszen

2 n \leq n + k

. Így

[n + 1, ..., n + k]

osztható

n

-nel, és természetesen

n + 1, ..., n + k - 1

-gyel is, tehát

[n, ..., n + k - 1]

osztója

[n + 1, ..., n + k]

-nak, amiből következik, hogy nem lehet az előbbi nagyobb.
A prímszámok eloszlására vonatkozó mély tételek segítségével belátható, hogy

n_{k} / k

tetszés szerinti 1-nél nagyobb

h

számnál kisebb lesz, amint

k

egy alkalmas (

h

-tól függő) korlátnál nagyobb.
2. Számolás közben sok olyan

n

-re találunk, amelyre

[n, ..., n + k - 1] = [n + 1, ..., n + k]

. Ez

n = k

-ra pl. csak akkor nem teljesül, ha

k

a 2-nek egy hatványa. De

k = 19

-re pl.

n = 19

-től

n = 22

-ig négy egymás utáni értékre teljesül az egyenlőség,

k = 210

-re, pedig

n = 213

-tól

n = 220

-ig nyolc egymás utáni esetben. Ezek után első pillanatra talán meglepően hat, hogy minden

k

-hoz legfeljebb véges sok esetben lehet két szomszédos lkkt egyenlő, pedig a (2) formula alapján ez legfeljebb az

\begin{matrix} n = \frac{k v_{n, k}}{v_{n + 1, k} - v_{n, k}} \end{matrix}

értékekre teljesül (és közülük az egész értékekre teljesül is). Mivel pedig

v_{n, k}

csak véges számú különböző értéket vehet fel, így csak véges számú megfelelő

n

létezik.

3. Az egész számok halmazát kiszíneztük száz színnel úgy, hogy mind a száz színt felhasználtuk és teljesül a következő: bárhogyan is választunk két

[a, b]

és

[c, d]

egyforma hosszú, egész végpontú intervallumot, ha

a

színe ugyanaz, mint

c

színe és

b

színe ugyanaz, mint

d

színe, akkor

[a, b]

és

[c, d]

teljes színezése megegyezik (azaz

0 \leq x \leq b - a, x

egész esetén

a + x

és

c + x

színe azonos). Bizonyítsuk be, hogy

- 1982

és

1982

színe különböző.

I. megoldás. A feladat feltételeiből következik, hogy az egész számok színezése 100 hosszúságú periódusokban ismétlődik az egész számegyenes mentén, és egy perióduson belül minden szín előfordul.

Ha ezt belátjuk, ebből következik, hogy két szám színe akkor és csak akkor egyezik meg, ha különbségük a 100 többszöröse.

- 1982

és 1982 tehát különböző színű, mert különbségük 3964, nem osztható 100-zal.

A színezés periodikus voltának belátásához előbb belátjuk, hogy

a) van olyan

A

és

d_{1}

természetes szám, amelyekre minden

A

-nál nagyobb szám színe megegyezik a

d_{1}

-gyel nagyobb száméval,
b) hasonlóan van olyan

B

és

d_{2}

természetes szám, hogy minden

- B

-nél kisebb egész színe megegyezik a

d_{2}

-vel kisebb száméval,
c) ezután belátjuk, hogy a két periodikus részszínezés az egész számegyenes egyetlen periodikus színezésének a része.

Az a) és b) részállítás bizonyítása ugyanazon gondolatmenettel történhet, elég tehát az a) állítás bizonyítását részletezni.
Nevezzük alapszámköznek azokat a számközöket, amelyeknek a kezdő és végső száma ugyanolyan színű és más egyező színű számpár nincs a számközben.
Egy alapszámköz legfeljebb 101 egész számot tartalmazhat, mert 100 színünk van, s így bármelyik számtól elindulva legkésőbb a 101-edik színe kell, hogy megegyezzék az előzők valamelyikével. Minden 101 egészet tartalmazó számköz tartalmaz is alapszámközt, hiszen az első számtól elindulva addig megyünk, míg először nem érünk a számköz egy korábbi számával egyező színű számához; ekkor ez a két egyező színű szám alapszámközt fog közre.
A természetes számok közt végtelen sok alapszámköz van, hiszen pl. a [

101 n

101 n + 100

]

(n = 0, 1, 2, ...)

számközök 101‐101 egészből állnak, s így mindegyik tartalmaz alapszámközt. Mivel egy alapszámköz legalább 2 és legfeljebb 101 egészet tartalmaz, kell olyan

d_{1}

egésznek lennie, hogy végtelen sok alapszámköz

d_{1} + 1

egészet (

d_{1}

különböző színűt) tartalmaz. Legyenek

[a_{i}, a_{i} + d_{1}]

(

i = 1, 2, ...

és

a_{i} \geq 0

d_{1} + 1

pozitív egészből álló alapszámközök. Megmutatjuk, hogy minden

A = a_{1}

-nél nagyobb

n

-re

n

és

n + d_{1}

színe megegyezik.
Legyen

n > A

. Mivel az

a_{i}

nem-negatív egészek sorozata végtelen, választhatjuk

j

-t úgy, hogy

a_{j} \geq n

teljesüljön. Az alapszámköz definíciójából következik, hogy az [

A

a_{j}

] és az [

A + d_{1}

a_{j} + d_{1}

] számközök kezdő számai is egyező színűek, a záró egészek is. Világos, hogy a két számköz ugyanannyi egészből áll és

j

választása szerint

n

az első számközhöz tartozik. A feladatnak a színezésre vonatkozó feltétele szerint ekkor következik, hogy

n + d_{1}

színe megegyezik

n

színével. Ezzel az a) állítást igazoltuk. Meggondolásainkat a negatív egészekből álló alapszámközökre alkalmazva kapjuk a b) állítás igazolását.

Az a), ill. b) állítás helyességéből természetesen az is következik, hogy ha

k

pozitív egész és

n > A

, ill.

m < - B

, akkor

n

és

n + k d_{1}

, ill.

m

és

m - k d_{2}

egyező színű.
A két periodikus rész kapcsolatának tisztázásához jegyezzük meg először is, hogy mind a két rész periodikus pl.

d_{1} \cdot d_{2}

szerint, hiszen csak a fenti állításban

k

helyett az első esetben

d_{2}

-t, a másodikban

d_{1}

-et kell írni. Megmutatjuk, hogy ez igaz az egész számegyenesre is.
Legyen ugyanis

r

tetszés szerinti egész,

u < - B

v > A

, továbbá

u \leq r \leq v

. Ekkor

u - d_{1} d_{2}

és

u

, ill.

v

és

v + d_{1} d_{2}

egyező színűek, így az [

u - d_{1} d_{2}

v

] és [

u

v + d_{1} d_{2}

] kielégítik a feladatban szereplő feltételeket, és az első tartalmazza

r

-et, így következik, hogy

r

és

r + d_{1} d_{2}

ugyanolyan színű.
Azt kell még belátnunk, hogy a legrövidebb periódushossz 100. Itt használjuk ki azt az eddig még nem értékesített tényt, hogy egy egyik végpontjától megfosztott alapszámköz csupa különböző színű pontból áll. Eszerint az

A

-nál nagyobb egészek

d_{1}

színnel vannak színezve, nem kevesebbel, mert tartalmaznak

d_{1} + 1

elemből álló alapszámközt, de nem is többel, hiszen színezésük

d_{1}

hosszúságú egyező periódusokból tevődik össze.
Ekkor azonban az egész számegyenes is

d_{1}

színnel van színezve, mert tetszés szerinti

r

egészhez van olyan

s

pozitív egész, hogy

r + s