Cím: Megjegyzések az F. 2355. feladathoz
Szerző(k):  Bakos Tibor 
Füzet: 1983/április, 153. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A megoldásban a közös csúcs nélküli élpárok merőleges állásának megmutatásakor látszólag nem használtuk ki teljesen a föltevést; csak azt, hogy a DE magasság a többi magasságok mindegyikét metszi. Ez a 3 metszéspont ‐ úgy tűnik ‐ különböző is lehetne (1. ábra), mintha a magasságok mintegy függetlenek volnának egymástól.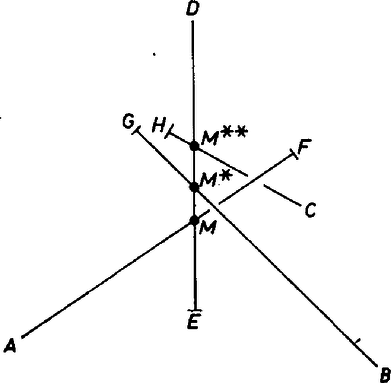

 

1. ábra
 
Elég lett volna azonban a feladatban inkább ezt föltenni: a tetraéder 3 magassága egy M pontban metszi egymást; már ekkor érvényes a vektoregyenlőség.
Ez a megfogalmazás azonban kevésbé tetszetős, mert nem szimmetrikus, ebben a negyedik magasságot mellőztük. Hasonló a helyzet a síkban is. Így igaz: két magasságvonal metszéspontján szükségképpen átmegy a harmadik, de tetszetősebb együtt szólni a háromról.
A 4 magasság kapcsolatához első meglátásunk: ha ‐ mint a megoldás 1. pontjában ‐ DE és AF-nek van közös pontja, M, akkor BG és CH is metszi egymást egy M* pontban. Ez azonban nem szükségképpen azonos M-mel! Bizonyításul belátjuk, hogy M létezéséhez nemcsak szükséges, hanem elegendő feltétel is, hogy DA⊥BC legyen.
Ha ugyanis azt tudjuk, hogy DA⊥BC, akkor ‐ mivel DE a szerkesztésnél fogva merőleges az ABC síkbeli BC-re ‐, azért a DAE sík is merőleges BC-re. Ugyanígy merőleges BC-re az ADF sík is. Ámde az A ponton át BC-re csak egy merőleges sík állítható, ezért D, A, E és F egy síkban vannak. Nem lehet azonban, hogy a DE és AF egyenesek párhuzamosak legyenek ‐ hiszen úgy az ABC és DBC lapsíkok is párhuzamosak lennének ‐, ennélfogva DE és AF metszik egymást.
Ebből már következik, hogy feltevésünk mellett a tetraéder B, C csúcsaiból húzott magasságok is metszik egymást egy M* pontban, hiszen a DA⊥BC tényben a két egyenes egyenrangú.
M* és M különböző lehet, erre példát mutat a 2. ábra. Tetraéderünk csúcsai egy szabályos négyoldalú hasáb csúcsai közül valók, ennélfogva lapjai egyenlő szárú háromszögek.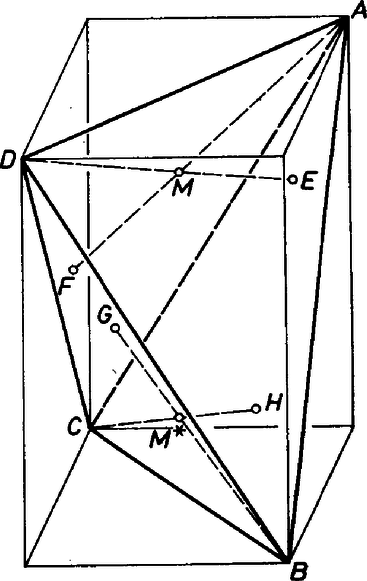
 

2. ábra
 

Tegyük föl most már, hogy a DE, AF magasságok közös M pontján a BG magasság is átmegy. Ekkor BG-vel AF-et párba állítva ‐ az előzők szerint ‐ egyfelől BA⊥CD, másfelől a másik két magasság, CH és DE is metszi egymást. Továbbá BG-nek DE-vel való metsződéséből BD⊥CA, valamint CH és AF is metszik egymást.
Átcsoportosítva e következményeket: egyrészt mind a három szemben fekvő élegyenespár merőleges helyzetű, másrészt a CH magasság DE-t is, AF-et is metszi. Nem lehet azonban, hogy CH-n így két különböző metszéspont adódjék, hiszen akkor CH benne lenne a DE és AF síkjában, vagyis a három magasság a DAC lapsíkban lenne. Így pedig a további 3 lapsík merőlegesen állna DAC-re és a B csúcs nem jönne létre. Eszerint CH is a DE és AF (és BG) közös M pontján megy át, amint előre kimondtuk.