Cím:	A középiskolások 1982. évi Számítástechnikai Versenyén kitűzött néhány feladat megoldása
Szerző(k):	Garádi János
Füzet:	1983/február, 68 - 73. oldal	PDF  |  MathML
Témakör(ök):	Szakmai cikkek

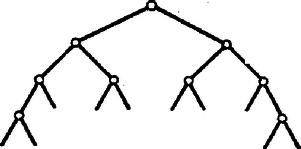
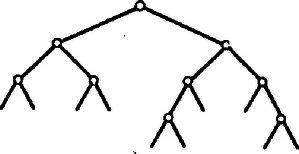
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A középiskolások 1982. évi Számítástechnikai Versenyén kitűzött néhány feladat megoldása   Az első forduló 2. feladata   A szovjet borítékokon az alábbi ábrán látható módon kell megadni az irányítószámok számjegyeit. Ez gyakorlatilag azt jelenti, hogy a tíz számjegy mindegyikét az itt látható $9$ vonalkából kell összeállítani. A leveleket osztályozó gép a programozó által előírt sorrendben lépésenként egy‐egy vonalkáról eldönti, hogy megvastagította-e a levél feladója. Adjunk meg egy eljárást, amelynek során a gép minél kevesebb vonalka megvizsgálásával dönti el, hogy milyen számjegy van a téglalapban. (Mindegyik kérdés függhet a korábbi kérdésekre kapott választói.) Képzeljük el, hogy a gépnek tízezer borítékot kell az utolsó számjegyük alapján szétválogatnia: mindegyik számjegy egyforma gyakorisággal (ezerszer) fordul elő. Hány vonalkát fog a gép végigvizsgálni a feladat megoldása során? Megoldás. Az osztályozó eljárást legszemléletesebben az ún. döntési fa felrajzolásával adhatjuk meg. 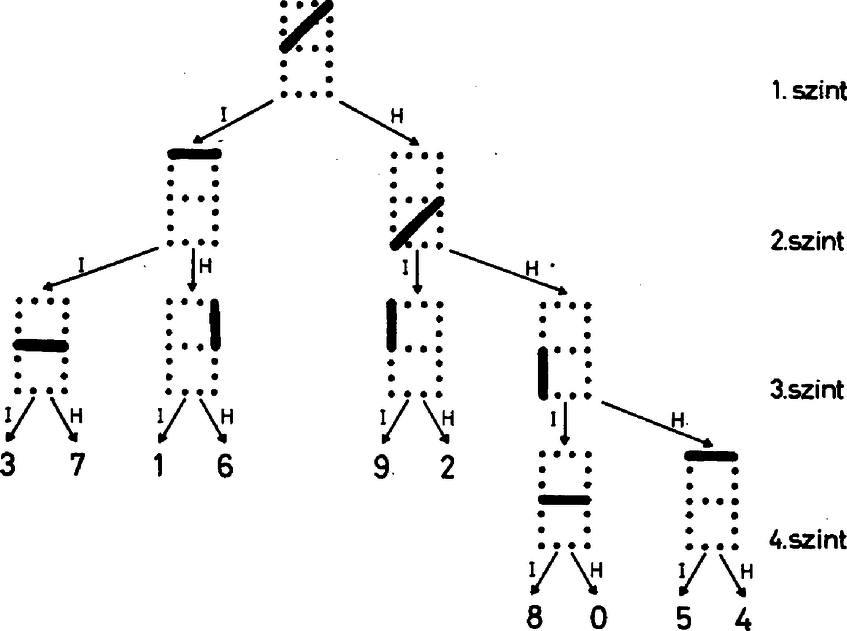Az ábra "olvasása'' nyilvánvaló: minden csomópontban a gép eldönti, hogy a megadott vonalka vastag-e vagy nem. Ha vastag, az $I$ (= igaz) betűvel jelzett ágon halad tovább, ha nem, akkor a $H$ (= hamis) ágon. Könnyen látható az is, hogy egy adott szám meghatározásához annyi vizsgálat szükséges, ahány szint van fölötte a döntési fában. Minthogy egy vizsgálatnak pontosan kétféle eredménye lehet és $2^3<10<2^4$, nincs olyan döntési fa, amelyben minden számjegy legfeljebb 3 vizsgálattal meghatározható. Az is igazolható, hogy a 3 vagy 4 vizsgálattal eredményre vezető döntési fákban mindig van 6 szám, amelynek meghatározása 3 vizsgálatot, míg a további 4 szám meghatározása 4 vizsgálatot igényel.   Ilyen döntési fák még: Ha mind a 10 számjegy azonos gyakorisággal fordul elő, akkor éppen ezek a döntési fák optimálisak. Példánkban $\left(6\cdot 3+4\cdot 4\right)\cdot 1000=34000$ vizsgálatot kell végezni.   Megjegyzések. 1.A számjegyek kódolása a szovjet borítékokon szerencsés, mert mint megmutattuk ‐ egyenletes előfordulási gyakoriság esetén ‐ szerkeszthető optimális döntési fa. 2. Ha a számjegyek különböző gyakorisággal fordulnak elő, nem feltétlenül a fenti ún. kiegyensúlyozott döntési fák az optimálisak.   Az első forduló 3. feladata   Adott egy $4$ alapműveletet végző, $9$ számjegyet megjelenítő zsebszámológép. Ennek segítségével kell kiszámolnunk, hogy $2^{1000}$ mennyi maradékot ad $1982$-vel osztva. A memória funkcióját egy papírlap és toll segítségével magunk látjuk el (a papíron műveleteket nem végezhetünk). Adjunk módszert a maradék minél kevesebb művelettel való kiszámolására. Állapítsuk meg, hogy eljárásunk során hány alapműveletet kell a gépnek elvégeznie.   I. megoldás. A feladat megoldásához a következő elemi tényt használjuk fel. Ha $a$, $b$, $c$, $d$ és $m$ természetes számok, $a$ és $b$, ill. $c$ és $d$ ugyanazt a számot adják maradékul $m$-mel osztva, akkor $a\cdot c$ és $b\cdot d$ is ugyanazt a maradékot adja.   Bontsuk fel $2^{1000}$-t a következő módon: $\begin{array}{c}{\displaystyle 2^{1000}=2^{40}\cdot 2^{960}={\left(2^{20}\right)}^2\cdot {\left(2^{15}\right)}^{64}\mathrm{.}}\end{array}$ (*) Először azt határozzuk meg, hogy $2^{40}$ mennyit ad maradékul 1982-vel osztva: $2^{40}=2^{20}{)}^2$ és $2^{20}=1048576$, ami még belefér a gépbe. Ezért 3 művelettel (egy maradékos osztással) megállapítható, hogy $2^{20}$ mennyit ad maradékul 1982-vel osztva: 98-at. A másik tényező, ${\left(2^{15}\right)}^{64}$ felírható $\begin{array}{c}{\displaystyle ({\left({\left({\left({\left({\left(2^{15}\right)}^2\right)}^2\right)}^2\right)}^3\right)}^3}\end{array}$ alakban. 3 művelettel megállapítjuk a $2^{15}$ maradékát, ezt négyzetre emeljük, 3 művelettel megállapítjuk a maradékot, majd ezt az utóbbi 4 lépést 5-ször megismételjük. 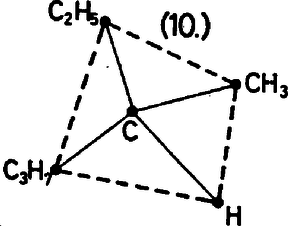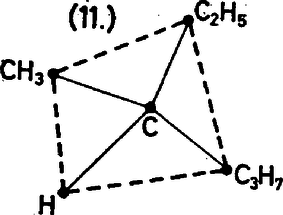Bár a feladat kitűzésében ez nem szerepel, illusztrációként elvégezzük a számításokat: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle 2^{15}}& {\displaystyle =32768}\hfill & {\displaystyle \text{maradék}:1056}\hfill \\ \hfill {\displaystyle {1056}^2}& {\displaystyle =1115136}\hfill & {\displaystyle \text{maradék}:1252}\hfill \\ \hfill {\displaystyle {1252}^2}& {\displaystyle =1567504}\hfill & {\displaystyle \text{maradék}:1724}\hfill \\ \hfill {\displaystyle {1724}^2}& {\displaystyle =2972176}\hfill & {\displaystyle \text{maradék}:1158}\hfill \\ \hfill {\displaystyle {1158}^2}& {\displaystyle =1340964}\hfill & {\displaystyle \text{maradék}:1132}\hfill \\ \hfill {\displaystyle {1132}^2}& {\displaystyle =1281424}\hfill & {\displaystyle \text{maradék}:1052}\hfill \\ \hfill {\displaystyle {1052}^2}& {\displaystyle =1106704}\hfill & {\displaystyle \text{maradék}:748.}\hfill \end{array}}$ Végül (emlékezzünk a (*) képletre!) a ${98}^2\cdot 748=7183792$-ről további 3 művelettel megállapítható, hogy 1982-vel osztva 1024-et ad maradékul. Ha feltételezzük, hogy 2 első 10 hatványát fejből tudjuk, akkor a $2^{20}$ és a $2^{15}$ kiszámítása egy‐egy műveletet igényel. Ezenkívül végeztünk 7 négyzetreemelést, 1 szorzást és 8 maradékos osztást (24 művelet), tehát összesen 34 műveletet. (Az utolsó lépésben egy kis szerencsénk volt: ${98}^2\cdot 748$ még befért a gépbe.)   II. megoldás. Az előző megoldás során az 1982 semmilyen speciális tulajdonságát nem használtuk ki. Vegyük azonban észre, hogy $1982=2\cdot 991$, és 991 prímszám. Ezért a Fermat‐tétel miatt $\left(2^{990}-1\right)$ osztható 991-gyel, azaz $\left(2^{991}-2\right)$ osztható 1982-vel. Minthogy $\begin{array}{c}{\displaystyle 2^{1000}=\left(2^{991}-2\right)\cdot 2^9+2\cdot 2^9\mathrm{,}}\end{array}$ ez utóbbi összeg első tagja osztható 1982-vel, tehát a keresett maradék 1024. Ez a megoldás végül nem igényelt egyetlen "gépi'' műveletet sem, mert fel tudtuk használni azt a körülményt, hogy az 1982 fele egy 1000-hez közeli, 1000-nél kisebb prímszám.   Megjegyzés. Azok a versenyzők, akik ezt a megoldást adták ‐ igen helyesen ‐ észrevették, hogy ez "nem számítástechnikai'' megoldás, mert nem lehet egyszerűen és áttekinthetően általános algoritmussá fejleszteni.   A második forduló 3. feladata   Van $N$ hírszerző. A felderítés befejezése után igyekeznek minél gyorsabban egymást értesíteni a szerzett információról. Egyszerre csak két hírszerző találkozhat, egy találkozáskor mindent elmondanak egymásnak,amit tudnak.   a) Adjunk meg olyan algoritmust, hogy $2N-3$ találkozás után minden hírszerző ismerje a teljes felderített információt. b) Ha $N\ge 4$, adjunk meg olyan algoritmust, amely ugyanezt a célt $2N-4$ lépésben valósítja meg.   Megoldás. Az $N=2$, 3 esetre a feladat megoldása nyilvánvaló. Az is világos, hogy $N\ge 4$ esetén elegendő a b) feladatot megoldani. Jelölje $h_1$, $h_2$, $\text{...}$, $h_N$ az $N$ hírszerzőt. $N=4$-re pl. a $\left(h_1\mathrm{,}{h}_2\right)$, $\left(h_3\mathrm{,}{h}_4\right)$, $\left(h_1\mathrm{,}{h}_3\right)$, $\left(h_2\mathrm{,}{h}_4\right)$ találkozósorozat után megtörténik a teljes információcsere. Ha $N>4$, jelöljünk ki egy 4-elemű "agytrösztöt'', pl. $h_1$, $h_2$, $h_3$, $h_4$. Az agytröszt tagjai találkoznak a maradék $N-4$ hírszerzővel. Ezek után egymás között 4 találkozás során kicserélik az általuk ismert (teljes) információt, majd az agytröszt tagjai $N-4$ találkozás során közlik a teljes információt a többi hírszerzővel. Látható, hogy lényegtelen az agytröszt tagjai közötti " munkamegosztás'' az információ begyűjtésében és terjesztésében.   A második forduló 4. feladata   Van egy $N$ tagú társaság. A társaság minden tagja legfeljebb $19$ másik tagot ismer. Feladatunk az, hogy a társaságot $2$ részre bontsuk, a "$7$-esek'' és a "$11$-esek'' klubjára úgy, hogy a "$7$-esek'' klubjukon belül legfeljebb $7$, a "$11$-esek'' klubjukon belül legfeljebb $11$ másik tagot ismerjenek. Egy matematikus a következő eljárást ajánlja: először osszuk tetszőlegesen két részre a társaságot, majd "fokozatosan'' lépésenként javítsuk ki az esetleges hibákat: ha valaki egy adott lépésben a "$7$-esek'' klubjához tartozik és ebben a klubban legalább $8$ ismerőse van, tegyük át a "$11$-esek'' klubjába, ill. fordítva, ha valakinek a "$11$-esek'' klubjában legalább $12$ ismerőse van, tegyük át a "$7$-esek'' közé. Így minden csere után megváltozik a klubok összetétele. Igaz-e, hogy ez az eljárás véges számú lépésben biztosan célra vezet?   Megoldás. A matematikusnak igaza van. Meg tudunk ugyanis adni olyan, a klubokba sorolástól függő természetes szám értékű függvényeket, amelyek értéke minden egyes javító lépés során legalább 1-gyel csökken. Ezért az algoritmus véges sok lépés után megszakad, ami azt jelenti, hogy a kívánt tulajdonságú klubok létrejöttek.   A feladatot két csapat oldotta meg helyesen, a két csapat két különböző ($C_1$ és $C_2$) függvényt adott meg: $C_1=7\times$ (a 11-esek klubján belüli ismeretségek száma) $+11\times$ (a 7-esek klubján belüli ismeretségek száma ill. $C_2$=(a klubokon belüli ismeretségek össz-száma) $+4\times$ (a 7-esek klubjának létszáma). Egyszerű számolás mutatja, hogy a $C_1$ függvény értéke 11-es $\to$ 7-es csere esetén legalább 7-tel, 7-es-$\to$ 11-es csere esetén legalább 11-gyel csökken. Mindkét függvény felhasználásával azt kapjuk, hogy ha kezdetben mindenki a 11-esek klubjába volt besorolva, akkor az eljárás véget ér, mégpedig legfeljebb annyi lépésben, mint amennyi a társaságban az összes ismeretségek száma.   A második forduló 5. feladata   Írjuk föl a $C_7{H}_{16}$ tapasztalati képleti szénhidrogén összes izomerjének szerkezeti képletét (a hidrogénatomok feltüntetése nélkül). $2$ vegyület izomerje egymásnak, ha azonos a tapasztalati képletük, de különböző a szerkezeti képletük, pl. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{C}}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{|}}\hfill \\ \hfill {\displaystyle \text{ C ‐ C ‐ C ‐ C ‐ C<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mi>M</mi><mi>M</mi></mphantom></math>}}\hfill & \hfill {\displaystyle \text{ C ‐ C ‐ C ‐ C ‐ C}}\hfill \\ \hfill {\displaystyle \text{ |}}\hfill & \hfill {\displaystyle \text{|}}\hfill \\ \hfill {\displaystyle \text{ C}}\hfill & \hfill {\displaystyle \text{C}}\hfill \\ \hfill {\displaystyle \text{ |}}\hfill & \hfill {\displaystyle }\hfill \\ \hfill {\displaystyle \text{ C}}\hfill & \hfill {\displaystyle }\hfill \end{array}}$ Ügyeljünk arra, hogy minden vegyület pontosan egyszer szerepeljen! Mennyi a kapott izomerek száma?   Megoldás. A feladatot helyesen megoldók észrevették, hogy az izomereket a bennük található leghosszabb szénlánc szerint rendezve érdemes felsorolni !