| Cím: | Kedvenc problémáim (1983. március) | ||
| Szerző(k): | Csirmaz László | ||
| Füzet: | 1983/március, 104 - 105. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Szakmai cikkek | ||
|
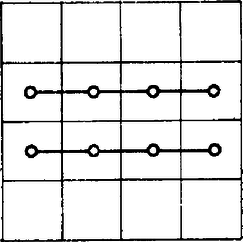
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Havonta egy-egy, számomra valamilyen oknál fogva kedves feladatot mondok el. Ezek megoldása, noha a középiskolában oktatott ismeretanyagnál többet nem kíván, mégis mély, igazi matematikusi gondolkodást igényel. A problémákra a megjelenést követő számban megoldást adok, azonban nem kívánok egyetlen problémát sem teljesen lezárni. Akár a feladatokkal, akár azok megoldásával kapcsolatban minden megjegyzést örömmel veszek. Bűvös négyzetben a sorokban, az oszlopokban, valamint a két átlóban álló számok összege megegyezik, ezt a közös összeget a bűvös négyzet állandójának szokás nevezni. A feladat feltételeinek megfelelően tegyük fel, hogy sikerült (egész) számot elhelyezni egy -es kockában úgy, hogy a kocka -es síkmetszetei (ugyanolyan állandójú) bűvös négyzetek legyenek. (Könnyű utánaszámolni, hogy összesen ilyen síkmetszet van.) Megmutatjuk, hogy ebben az esetben a kockába beírt számok között van két egyenlő ‐ ez bizonyítja állításunkat. Elsőként megmutatjuk, hogy egy -es bűvös négyzetben a négy "sarokelem'' összege is a bűvös állandót adja. Valóban, adjuk össze az 1a ábrán megjelölt mezőkben álló számokat, mindegyiket annyiszor, ahány pont a megfelelő mezőben szerepel. Látható, hogy az összeg a bűvös állandó négyszerese.
|