| Cím: | Az 1982. évi (23.) Nemzetközi Fizikai Diákolimpia feladatai | ||
| Füzet: | 1982/november, 161 - 168. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Nemzetközi Fizika Diákolimpia | ||
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.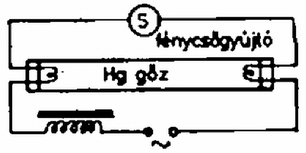 1. ábra 1. Egy fénycsővet Hz-es váltakozó áramú hálózatra kapcsolunk (1. ábra). Működés közben a kővetkező adatokat mérjük: Számításainkban magát a fénycsővet tiszta ohmikus ellenállásúnak tekinthetjük. a) Mekkora a fojtótekercs b) Mekkora a c) Mekkora az áramkör által felvett teljesítmény? d) Azon kívül, hogy a fojtótekercs korlátozza az áramot, más fontos szerepe is van. Mi ez? Megjegyzés. A fénycsőgyújtó szerkezet egy olyan kapcsoló, amely a hálózati feszültség bekapcsolásakor zárja, majd nyitja az áramkört, és ezután nyitva is marad, ha a fénycső már világít. e) Rajzoljuk meg a működő állapotban levő fénycső fényintenzitását mint az idő függvényét kvantítatív időskálával! f) Miért kell csupán egyszer begyújtani a fénycsövet, noha a váltakozó áram szabályos időközönként átmegy a nulla értéken? g) A gyárban adott útmutató szerint egy kb. h) Vizsgáljuk meg az adott fénycső két felét az adott spektroszkóppal. (A fénycső egyik felén van csak lumineszkáló bevonat.) Magyarázzuk meg a két spektrum közti különbséget! Megoldás. (A továbbiakban a hivatalos pontozást is feltüntetjük.) Az a), b) és c) ponthoz a váltakozó áramra vonatkozó összefüggések érvényesek. a) A teljes impedancia Ebből az ismert összefüggéssel b) c) A teljesítmény d) Amikor a gyújtó zár, áram folyik rajta és ez izzítja a fénycső két végén levő izzószálat. A gyújtó kikapcsolásakor a tekercsen nagy feszültség indukálódik, ami begyújtja a csövet. A működési folyamat fenntartásához a hálózati feszültség már elegendő. 1 pont e)Az 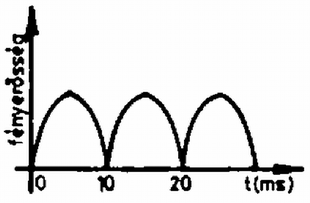 2. ábra f) A begyújtáskor az izzószál és az első impulzus sok iont és szabad elektront hoz létre. Ezeknek a semlegesítődéséhez elég sok idő kell. Az újragyújtáshoz szükséges töltéshordozók a feszültség újbóli megjelenésekor még rendelkezésre állnak. 1 pont g) A Ha minden második fénycső elé ilyen "fázisjavító'' kondenzátort kötünk, akkor nem lesz eredő fázistolás. A nagy fázistolás veszteségeket okoz a tápvezetéken, és az erőművekben. Ezek a kondenzátorok ezt szüntetik meg. 2 pont h) A cső lumineszkáló bevonattal be nem borított felén a Hg-gőz vonalas spektruma látható. A bevonattal ellátott részben ezen kívül még folytonos spektrumot látunk. A Hg ultraibolya sugárzása ugyanis gerjeszti a szilárd bevonatot, amely mint általában a szilárd anyagok, folytonos spektrummal rendelkezik. 1 pont 2. Egy drótból készült ruhafogas kis amplitúdójú lengéseket végez az ábra síkjában a lerajzolt egyensúlyi helyzetek körül (3. ábra). Az a) és a b) helyzetben a fogas hosszú oldala vízszintes. A másik két oldal egyenlő hosszú. A lengésidő mindhárom esetben azonos. Hol a tömegközéppont és mekkora a lengésidő? (Az ábra a megadott adatokon kivül információt nem tartalmaz.) 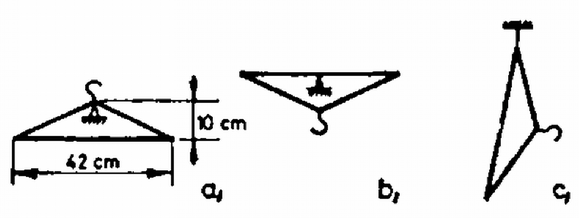 3. ábra Megoldás. A fizikai inga lengésideje: ahol Az előző két összefüggés alapján 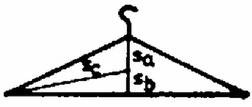 4. ábra A gyökök és együtthatók közti összefüggés alapján amiből 3. A a) Milyen b) A ballont a talajhoz rögzítjük és a benne levő levegőt állandóan c) A ballont alul bekötjük, de a benne levő levegő állandóan d) A Megoldás. a) Először kiszámítjuk a ballonban levő levegő sűrűségét lebegéskor. A lebegés feltétele: Az egyesített gáztörvényhől, figyelembe véve, hogy a térfogat állandó: ahol b) A kötelet feszítő erő ahol Mivel ahol A ballon addig emelkedik, amíg a súlya egyenlő lesz a felhajtóerővel: ahol Ebből A barometrikus magasságformula szerint (1. Budó Ágoston: Kísérleti fizika) ahol Számadatokkal: d) Ha a ballont egyensúlyi helyzetéből kis mértékben kimozdítjuk, a visszatérítő erő lineáris lesz. 0,25 pont Ennek hatására harmonikus rezgőmozgást végez. 1 pont A hőlégballon mozgását erősen akadályozza a levegő közegellenállása, ezért a rezgőmozgás csillapított. 0,5 pont Kísérleti feladatok 4. A méréshez csak az adott bikonvex lencse, síktükör, a csepegtető edényben levő víz, az optikai tárgy (ceruza) és az állítható szorítóval ellátott állvány használható. 1. Halározzuk meg 2. Halározzuk meg a lencse anyagának törésmutatóját! A víz törésmutatója Megoldás. Hogy az Helyezzük a síktükröt az állvány aljára, és fektessük rá a lencsét. A szorítóban levő tárgy (a ceruza) képét felülről látjuk. 1 pont A kép helyét kell pontosan meghatározni. Ez akkor lehetséges, ha a tárgyat úgy helyezzük el, hogy képével egybeessék. 0,5 pont Ebben az esetben fejünket mozgatva a tárgy és a kép relatív helyzete nem változik. 1 pont 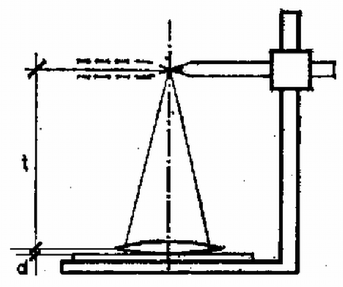 5. ábra Ekkor egy lencserendszerrel van dolgunk, amelynek fókusztávolsága A kép és a lencse vagy tükör távolságát többször lemérve láthatjuk, hogy a statisztikus hiba nincs egy százalék. A távolságnak Szisztematikus hiba már van, mivel a lencse vastagsága  6. ábra A törésmutató meghatározásához még egy összefüggés kell, mert a bikonvex lencsére felírt összefüggéshez jutunk, ahol képlet határozza meg. A törésmutatóra az 5. A csúszásmentesen gördülő henger mozgását felbonthatjuk egy tengely körüli forgásra és a tömegközéppont vízszintes transzlációjára. Ebben a kísérletben közvetlenül csupán a transzlációs gyorsulás és az azt létrehozó erők határozhatók meg. Az Mielőtt a mérést elkezdjük, állítsuk be a deszkát vízszintesre papírdarabokkal. A jelen célnak megfelel, ha a deszka nem lejt a) Határozzuk meg kísérletileg a henger különböző b) A kapott c) Ábrázoljuk az d) Mi a következménye annak, ha a deszka nem vízszintes? e) Írjuk le a mellékmennyiségek meghatározását és a szükséges további beállításokat is! Adjuk meg, hogy a rossz beállítás hogyan befolyásolja az eredményeket! 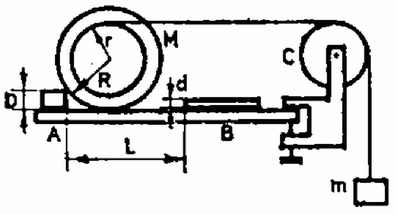 7. ábra A kővetkező mennyiségek adottak: A csiga Megoldás. Mielőtt elkezdjük a mérést, a fonalat vízszintesre és a mozgás irányába kell állítani. Ezt a csiga A fonál beállítását elég szemmérték alapján elvégezni, mivel az eltérési hiba koszinuszával kell ilyen esetben korrekciót végezni, és a koszinusz függvény nem túl nagy szögekre még közel Vigyázni kell a sík vízszintes beállítására. Az A henger elmozdulása a 7. ábra alapján A megadott számértékekkel A gyorsulásokat az képletből lehet kiszámítani. Különböző Az időmérés pontossága az adatok alapján A táblázat már feltünteti a súrlódási erő értékét is. 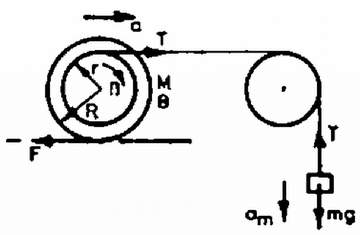 8. ábra Az (1), (2) és (5) egyenletből összefüggést. Ebből számítottuk ki az A A grafikonból két lényeges információt nyerhetünk. Egyrészt lineáris az összefüggés, másrészt az erő előjelet vált. Ez érthető is. Ha 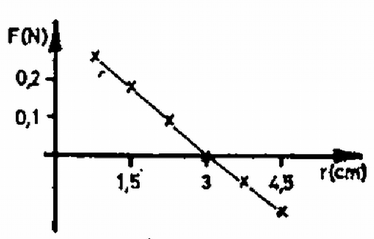 9. ábra |