Cím:	1982. évi fizika OKTV feladatai
Füzet:	1982/október, 81 - 88. oldal	PDF  |  MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az 1982. évi középiskolai tanulmányi verseny feladatai   Az I. forduló feladatai   1. Egyenlőkarú emeld egyik végére elhanyagolható tömegű korong van csapágyazva (1. ábra). A korongról lelógó fonál végeire $m_0$ és $m$ tömegű testeket akasztottunk. Az emelő végén $m_0$ tömegű test függ. Mekkora legyen a fonál másik végén függő test $m$ tömege, hogy az emelőrúd vízszintes egyensúlyi helyzetben maradjon? (Párkányi László) 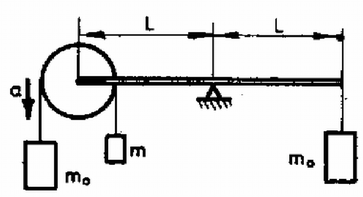    1. ábra   Megoldás. A fonálon függő, összesen $m_0+m$ tömegű testeket $m_{0}g-mg$ erő gyorsítja, ezért a gyorsulás: $\begin{array}{c}{\displaystyle a=g\cdot \frac{m_0-m}{m_0+m}\mathrm{.}}\end{array}$ A fonalakban ébredő erő $\begin{array}{c}{\displaystyle m_0\left(g-a\right)=m_{0}g\cdot \frac{2m}{m_0+m}\mathrm{.}}\end{array}$ A két fonálerő eredője ennek kétszerese, és ez tart egyensúlyt az emelő jobb oldali végén ható $m_{0}g$ erővel: $\begin{array}{c}{\displaystyle \frac{4m{m}_{0}g}{m_0+m}=m_{0}g\mathrm{.}}\end{array}$ Innen: $\begin{array}{c}{\displaystyle m=\frac{m_0}{3}\mathrm{,}}\end{array}$ és a gyorsulás $\begin{array}{c}{\displaystyle a=g/2.}\end{array}$   2. Egy körlejtő sugara $OA=0\mathrm{,}8$ méter hosszú. Középpontja alatt $OB=0\mathrm{,}48$ méter mélyen, a $B$ pontban rögzítjük egy rugó egyik végét (2. ábra). A rugó eredeti hossza $L=0\mathrm{,}32\text{<span style="font-style: italic;">m</span>}$ és rugóállandója $D=75\text{<span style="font-style: italic;">N/m</span>}$. A rugó másik végét vízszintesen kihúzzuk a lejtőn levő $C$ pontig, itt egy $m=3\mathrm{,}2\text{<span style="font-style: italic;">kg</span>}$ tömegű testet akasztunk rá, és a testet elengedjük. A súrlódás elhanyagolható, $g=10{\text{<span style="font-style: italic;">m/s</span>}}^2$.   a) Mekkora sebességgel halad át a test a lejtő legalsó pontján? b) Mekkora erő nyomja ekkor a lejtőt? (Vermes Miklós) 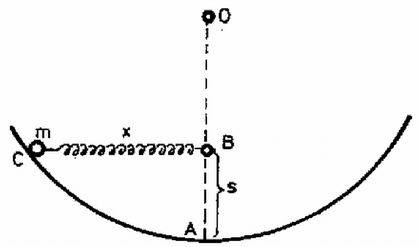    2. ábra   Megoldás. A lejtő legalján, az $A$ pontban a rugó hossza az eredeti hosszúság, mert $s=AB=0\mathrm{,}32$ m, így itt nem marad a rugóban rugalmas energia. A súlyerő munkavégzésének és a rugó munkavégzésének az összege egyenlő a mozgási energiával: $\begin{array}{c}{\displaystyle mg\cdot s+\left(1/2\right)D{\left(x-L\right)}^2=\left(1/2\right)m{v}^2\mathrm{,}}\end{array}$ ahol $x$ a $C$ pontig kihúzott rugó hossza, azaz a $BC$ félhúr hossza, amely az adatokkal: $x=0\mathrm{,}64$ m. Az adatokat behelyettesítve a sebesség $v=2\mathrm{,}97$ m/s. A legalsó helyzetben a rugó hossza egyenlő az eredeti $L$ hosszúsággal, a lejtőre az $mg$ súlyerő és $m{v}^2/r$ középpont felé mutató erő hat: $\begin{array}{c}{\displaystyle F=mg+m{v}^2/r=67\mathrm{,}2\text{ N}\mathrm{.}}\end{array}$   3. Egy $M$ tömegű, $R$ sugarú henger ált egy szegletben (3. ábra). A hengerre csavart fonál egy kis csigán van átvetve és végéről $m$ tömegű test lóg le. A $\mu$ csúszási súrlódási együttható a talajon és a falon ugyanakkora. Mekkora gyorsulással mozog a fonál végére akasztott test? Számadatok: 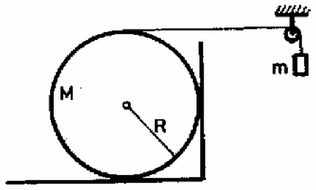$\begin{array}{c}{\displaystyle \mu =0\mathrm{,}\mathrm{5,}m=11\text{ kg}\mathrm{,}M=8\text{ kg}\mathrm{,}R=0\mathrm{,}4\text{ m}\mathrm{,}g=10{\text{ m/s}}^2\mathrm{.}}\end{array}$ (Wiedemann László)     3. ábra   Megoldás. A $m$ tömegű test a gyorsulással süllyed, tehát a fonálerő (4. ábra): 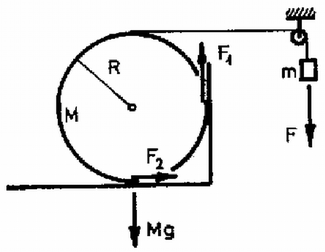$\begin{array}{c}{\displaystyle F=mg-ma\mathrm{.}}\end{array}$ A hengerre a fonálerő, a súlyerő és az $F_1$ és $F_2$ súrlódási erők hatnak, amelyekre igaz: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle F_1=\mu \left(F+F_2\right)\mathrm{,}}\hfill & \text{(<mn>1</mn>)}\\ \hfill {\displaystyle F_2=\mu \left(Mg-F_1\right)\mathrm{.}}\hfill & \text{(<mn>2</mn>)}\end{array}}$   4. ábra   A henger szöggyorsulása $\beta =a/R$, a tehetetlenségi nyomatéka $\Theta$. A henger mozgásegyenlete: $\begin{array}{c}{\displaystyle FR-F_{1}R-F_{2}R=\Theta \cdot \left(a/R\right)\mathrm{.}}\end{array}$ (3) Az (1)‐(3) egyenletrendszert kell megoldanunk. (1)-ből és (2)-ből következik,hogy ${\displaystyle \begin{array}{cc}\hfill {\displaystyle F_1=\frac{\mu \left(F+\mu Mg\right)}{1+{\mu }^2}\mathrm{,}}\hfill & \text{(<mn>4</mn>)}\\ \hfill {\displaystyle F_2=\frac{\mu \left(Mg-\mu F\right)}{1-{\mu }^2}\mathrm{.}}\hfill & \text{(<mn>5</mn>)}\end{array}}$ (4)-et, (5)-öt és a fonálerő értékét behelyettesítve (3)-ba a gyorsulást kifejezhetjük: $\begin{array}{c}{\displaystyle a=g\cdot \frac{\left(m/M\right)\cdot \left(1-\mu +2{\mu }^2\right)-\mu \left(1+\mu \right)}{\left(m/M\right)\cdot \left(1-\mu +2{\mu }^2\right)+\left(1+{\mu }^2\right)\cdot \Theta /\left(M{R}^2\right)}\mathrm{.}}\end{array}$ Számadatainkkal $a=3\mathrm{,}125{\text{ m/s}}^2$, $F_1=46\mathrm{,}25\text{ N}$, $F_2=16\mathrm{,}875\text{ N}$, $F=75\mathrm{,}625\text{ N}$. A gyorsulás független a henger sugarától. Ha az $a$-ra kapott eredményt nullával tesszük egyenlővé, akkor megkapjuk annak feltételét, hogy a henger ne kezdjen forogni: $\begin{array}{c}{\displaystyle \frac{m}{M}=\frac{\mu \left(1+\mu \right)}{\left(1-\mu +2{\mu }^2\right)}\mathrm{.}}\end{array}$   4. Egy $160\text{<span style="font-style: italic;"> g</span>}$ tömegű, $5{\text{<span style="font-style: italic;"> cm</span>}}^2$ alapterületű, vékony falú hengert dugattyújához erősített fonálon úgy tartjuk víz alatt lógva, hogy feneke $10\text{<span style="font-style: italic;"> m</span>}$-re van a víz felszíne alatt (5. ábra). A hengerben a légoszlop hossza $20\text{<span style="font-style: italic;"> cm</span>}$. A fonalat lassan húzzuk felfelé. Milyen mélyen van a henger, amikor lebegni kezd? A légköri levegő nyomása $10{\text{<span style="font-style: italic;"> N/cm</span>}}^2$, $g=10{\text{<span style="font-style: italic;"> m/s</span>}}^2$; a dugattyú súrlódása elhanyagolható. (Vermes Miklós) 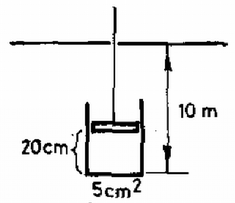    5. ábra   Megoldás. A henger és a dugattyú között a súrlódás elhanyagolható, tehát közöttük közvetlen erőhatás nincs. Ha valamely $h$ mélységben a fonállal tartva nyugalomban van a rendszer, akkor a hengerre és a dugattyúra külön kell felírni az egyensúly feltételét. A hengerre az $mg$ súlyerő, a bezárt levegő $pA$ nyomóereje, a $p_l$ külső légnyomás és a víz hidrosztatikai nyomásából származó erő hat. Tehát az egyensúly feltétele: $\begin{array}{c}{\displaystyle mg+pA=p_{l}A+h\varrho gA\mathrm{,}}\end{array}$ (1) ahol $h$ a henger aljának a felszíntől mért távolsága. A dugattyú elhanyagolható tömegű, így az egyensúly feltétele a dugattyúra: $\begin{array}{c}{\displaystyle F+pA=p_{l}A+\left(h-l\right)\varrho gA\mathrm{.}}\end{array}$ (2) ahol $F$ a fonálban ébredő erő, $l$ pedig a $h$ mélységben levő hengerbe bezárt levegő hossza. Az (1) egyenlet megadja a $p=p\left(h\right)$ függvényt. Ennek és a Boyle‐Mariotte-törvénynek a segítségével az $l$-t kiszámíthatjuk, a kezdeti adatok ismeretében. (A kezdeti adatokat 0 indexszel jelöljük): $\begin{array}{c}{\displaystyle l=\frac{p_0{l}_0}{h\varrho g+p_l-\left(mg/A\right)}\mathrm{.}}\end{array}$ (3) A lebegés megegyezik az $F=0$ feltétellel, tehát abban a $h$ mélységben lebeg a rendszer, ahol $\begin{array}{c}{\displaystyle pA=p_{l}A+\left(h-l\right)\varrho gA\mathrm{.}}\end{array}$ (4) Beírva ide a (3) összefüggést, a rendezés után kapjuk: $\begin{array}{c}{\displaystyle h\varrho g=\frac{p_0{l}_0}{mg}\cdot A-p_0+\frac{mg}{A}\mathrm{.}}\end{array}$ Behelyettesítve a $h_0=10\text{ m}$, $p_l=10{\text{ N/cm}}^2$, $m=160\text{ g}$, $l_0=20\text{ cm}$, $A=5{\text{ cm}}^2$ és $\begin{array}{c}{\displaystyle p_0=h_0\varrho g+p_l-mg/A=19\mathrm{,}68{\text{ N/cm}}^2}\end{array}$ értékeket, $\begin{array}{c}{\displaystyle h=2\mathrm{,}62\text{ m}}\end{array}$ adódik.   A II. forduló feladatai   1. Egy $\alpha$ hajlásszögű, $M$ tömegű lejtő súrlódásmentesen mozoghat a vízszintes talajon (6. ábra). A nyugvó lejtőre függőlegesen ráejtünk egy $m$ tömegű, $v$ sebességű testet és ez rugalmasan ütközik a lejtővel. Mekkora $u$ sebességgel és a vízszinteshez képest mekkora $\phi$ szögben hagyja el a test a lejtőt és mekkora $c$ sebességre tesz szert a lejtő? Számadatok: $\alpha =37\mathrm{,}{87}^{\circ }$, $m=6\text{<span style="font-style: italic;"> kg</span>}$, $M=18\text{<span style="font-style: italic;"> kg</span>}$, $v=14\text{<span style="font-style: italic;"> m/s</span>}$. (Légrádi Imre) 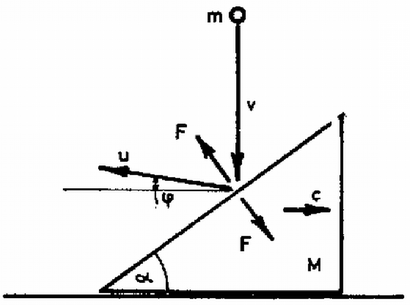    6. ábra   Megoldás. Hasson az ütközés során $\Delta t$ ideig a lejtőre merőlegesen $F$ erő. Ekkor a $m$ tömegű test impulzusának a függőleges irányú megváltozása: $\begin{array}{c}{\displaystyle F\cdot \Delta t\text{cos}\alpha =mu\text{sin}\phi -\left(-mv\right);}\end{array}$ míg az $m$ tömegű test impulzusának a vízszintes irányú megváltozása: $\begin{array}{c}{\displaystyle F\cdot \Delta t\text{sin}\alpha =mu\text{cos}\phi \mathrm{.}}\end{array}$ A lejtő impulzusát az impulzusmegmaradás törvényéből kapjuk meg: $\begin{array}{c}{\displaystyle mu\text{cos}\phi =Mc\mathrm{.}}\end{array}$ Az energiamegmaradás törvénye szerint $\begin{array}{c}{\displaystyle m{v}^2/2=\left(m{u}^2/2\right)+\left(M{c}^2/2\right)\mathrm{.}}\end{array}$ Vezessük be a $k=m/M$ jelölést és küszöböljük ki az $F\Delta t$ impulzusváltozást a fenti egyenletből. Ekkor a ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{ctg}\alpha =\text{tg}\phi +\frac{v}{u\text{cos}\phi }\mathrm{,}}\hfill & \text{(<mn>1</mn>)}\\ \hfill {\displaystyle ku\text{cos}\phi =c\mathrm{,}}\hfill & \text{(<mn>2</mn>)}\\ \hfill {\displaystyle k{v}^2=k{u}^2+c^2\mathrm{.}}\hfill & \text{(<mn>3</mn>)}\end{array}}$ egyenletrendszert kapjuk. Ezt az egyenletrendszert kell megoldani $\phi$-re, $u$-ra és $c$-re. Először (2)-ből kifejezzük $c$-t és (3)-ba helyettesítjük: $\begin{array}{c}{\displaystyle k{v}^2=k{u}^2+k^2{u}^2\text{cos}{}^2\phi \mathrm{,}}\end{array}$ innen az ismeretlen $u$: $\begin{array}{c}{\displaystyle u=\frac{v}{\sqrt[]{1+k\text{cos}{}^2\phi }}}\end{array}$ (4) $u$ ezen értékét (1)-be helyettesítve egyenletet kapunk $\phi$-re: $\begin{array}{c}{\displaystyle \text{ctg}\alpha =\text{tg}\phi +\frac{\sqrt[]{1+k\text{cos}{}^2\phi }}{\text{cos}\phi }\mathrm{.}}\end{array}$ A megfelelő trigonometriai összefüggések felhasználásával az eredmény a keresett $\phi$ szögre: $\begin{array}{c}{\displaystyle \text{tg}\phi =\left(1/2\right)\cdot \left[\text{ctg}\alpha -\left(1+k\right)\text{tg}\alpha \right]\mathrm{.}}\end{array}$ Ez a szög független $v$-től. Ha $\phi$ megvan, (4)-ből kapjuk az $u$ sebességet és (2)-ből $c$-t: $\begin{array}{c}{\displaystyle c=\frac{k\text{cos}\phi }{\sqrt[]{1+k\text{cos}{}^2\phi }}\cdot v\mathrm{.}}\end{array}$ Számadatainkkal $\text{sin}\alpha =3/5$, $\text{cos}\alpha =4/5$, $\text{tg}\alpha =3/4$, $k=1/3$. Az eredmény $\text{tg}\phi =1/6=0\mathrm{,}1667$, $\phi =9\mathrm{,}{46}^{\circ }$, $u=2\sqrt[]{37}=12\mathrm{,}166$ m/s, $c=4$ m/s. A visszapattanó test sebessége $43\mathrm{,}{67}^{\circ }$-os szöget zár be a lejtő merőlegesével. Rögzített lejtő esetében ennek a szögnek is $36\mathrm{,}{87}^{\circ }$-osnak kellett volna lennie.   2. R sugarú henger két végére $r=R/3$ sugarú korongokat erősítünk (7. ábra). A hengert a korongokra feltekert fonalakra függesztjük és elengedjük. A henger palástján nyomdafestékes betűk vannak körös‐körül elhelyezve. Az a feladatunk, hagy ezt a szöveget hibátlanul nyomtassuk le egy függőleges falra, amely mellett a henger mozog. Mekkora gyorsulással kell a fonál végét mozgatnunk? Az $r$ sugarú korongok tömegétől eltekintünk. (Nagy László)   Megoldás. A hibátlan nyomtatáshoz szükséges, hogy a henger csúszás nélkül gördüljön a falon. Ennek érdekében a fonalat a kezünkkel $a_x$ gyorsulással kell lefelé engednünk. Mozogjon a henger tengelye $a$ gyorsulással lefelé. A mozgásegyenlet 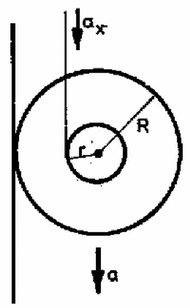$\begin{array}{c}{\displaystyle mg-F=ma\mathrm{,}}\end{array}$ (1) ahol $F$ a fonálerő. Az $Fr$ forgatónyomaték hatására a $\Theta$ tehetetlenségi nyomatékú henger $\beta$ szöggyorsulással forog: $\begin{array}{c}{\displaystyle Fr=\beta \Theta \mathrm{.}}\end{array}$ (2) A henger kerületi gyorsulása $\begin{array}{c}{\displaystyle a=a_x+\beta \cdot r\mathrm{.}}\end{array}$ (3)   7. ábra   A csúszás nélküli legördülés feltétele: $\begin{array}{c}{\displaystyle a=\beta R\mathrm{.}}\end{array}$ Az (1)‐(4)egyenletrendszer megoldása: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle a_x}& {\displaystyle =\frac{r\left(R-r\right)m}{\Theta +rRm}\cdot g\mathrm{,}}\hfill \\ \hfill {\displaystyle F}& {\displaystyle =\frac{mg}{1+\left(rRm/\Theta \right)}\mathrm{,}}\hfill \\ \hfill {\displaystyle \beta }& {\displaystyle =\frac{mgr}{\Theta +rRm}\mathrm{,}}\hfill \\ \hfill {\displaystyle a}& {\displaystyle =\frac{mrR}{\Theta +rRm}\cdot g\mathrm{.}}\hfill \end{array}}$ Behelyettesítve a henger $\Theta =\left(1/2\right)m{R}^2$ tehetetlenségi nyomatékát és a megadott $r/R=1/3$ sugárarányt, kapjuk, hogy $a_x=4g/15$, $F=0\mathrm{,}6mg$, $\beta =0\mathrm{,}4g/R$. $a=0\mathrm{,}4g$. Felmerülhet az a kérdés is, hogy a henger a túlsó oldalon levő falra nyomtassa le hibátlanul a szöveget. Ekkor a kötélvéget felfelé kell mozgatnunk $a_y$ gyorsulással. Az egyenletrendszer az előbbihez hasonlóan alakul, az eredmény: $a_y=8g/3$, $F=3mg$, $\beta =2g/R$, $a=2g$.   3. Az $L$ önindukciójú tekercs, $C$ kapacitású kondenzátor és a két, egymással egyenlő $R_C=R_L=R$ ellenállás adott értékek a 8. ábra szerinti kapcsolásban. Mekkora az a legnagyobb feszültség, amely alkalmas frekvencia esetén $A$ és $B$ pontok között felléphet? Adatok: a) $R=1\text{ k}\Omega$, $c=0\mathrm{,}1\mu \text{F}$, $L=0\mathrm{,}1$ H; b) $$\begin{gathered} R= \\ =1\text{ k}\Omega \end{gathered}$$, $C=0\mathrm{,}1\mu \text{F}$, $L=0\mathrm{,}4$ H.   (Dr. Bodó Zalán) 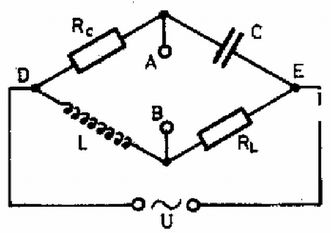    8. ábra   Megoldás. A szokásos eljárás szerint ki kell számítani mindegyik ágban az áramerősség amplitúdóját és fázisát. Azután ki kell számítani ezek felhasználásával az $AE$ és $BE$ pontokra jutó feszültségkülönbségeket (mint az idő függvényeit) és ezek különbsége adja az $AB$ között jelentkező $U_x$ feszültséget. 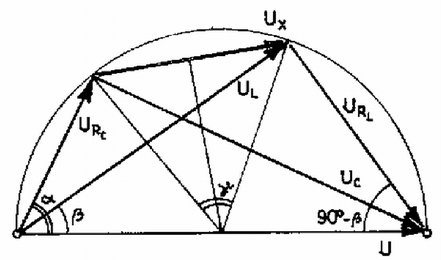  9. ábra   Áttekinthetőbb a megoldás a feszültségek vektorábrája alapján (9. ábra). A felső ágban az adott $U$ feszültség $U_{R_C}$-nek és $U_C$-nek az összege, $U_{R_C}$, és $U_C$ merőleges egymásra, és így egy félkörbe rajzolható. Az alsó ágban ugyanaz az adott $U$ feszültség $U_L$ és $U_{R_C}$ összege, $U_L$ és $U_{R_L}$ szintén merőlegesek egymásra, és berajzolhatók az előbbi félkörbe. Az ábrán levő szögekre írhatjuk: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{tg}\alpha }& {\displaystyle =\frac{U_C}{U_{R_C}}=\frac{I_1/\omega C}{I_1\cdot R}=\frac{1}{\omega CR}\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{tg}\beta }& {\displaystyle =\frac{U_{R_L}}{U_L}=\frac{I_{2}R}{I_2{\omega }_L}=\frac{R}{\omega L}\mathrm{.}}\hfill \end{array}}$ $I_1$ és $I_2$ a felső, ill. az alsó ágban folyó áramot jelöli. A keresett $U_x$ feszültséget a derékszögek csúcsait összekötő vektor adja. Ugyanis a 8. ábra $D-A-B-E$ (vagy $D-B-A-E$) útján végigmenve is $U$ a feszültség. $U_x$ akkor maximális, ha a hozzá tartozó $\gamma$ középponti szög maximális, ez pedig ($\alpha -\beta$) kétszerese. $\begin{array}{c}{\displaystyle \text{tg}\frac{\gamma }{2}=\text{tg}\left(\alpha -\beta \right)=\frac{\text{tg}\alpha -\text{tg}\beta }{1+\text{tg}\alpha \text{tg}\beta }=\frac{\left[1/\left(\omega CR\right)\right]-\left[R/\left(\omega L\right)\right]}{1+\left[1/\left({\omega }^{2}LC\right)\right]}=\frac{1}{R}\cdot \frac{L-C{R}^2}{CL\omega +\left(1/\omega \right)}\mathrm{.}}\end{array}$ Ez a tört akkora legnagyobb, amikor a nevezője $y=CL\omega +\left(1/\omega \right)$ a legkisebb. Ennek feltétele: $\begin{array}{c}{\displaystyle \frac{\text{d}y}{\text{d}\omega }=CL-\frac{1}{{\omega }^2}=0\text{alapján}\omega =\frac{1}{\sqrt[]{LC}}\mathrm{.}}\end{array}$ (Ekkor $y$ valóban minimális.) Ebben az esetben $\begin{array}{c}{\displaystyle \text{tg}\frac{\gamma }{2}=\text{tg}\left(\alpha -\beta \right)=\frac{1}{R}\cdot \frac{L-C{R}^2}{2\sqrt[]{LC}}\mathrm{.}}\end{array}$ A keresett feszültség: $\begin{array}{c}{\displaystyle U_x=\left(U/2\right)g\text{sin}\left(\gamma /2\right)\mathrm{.}}\end{array}$ A vektorábrában $U_x$ hajlásszöge a vízszinteshez adja a fázisszöget, amely a maximális feszültség esetében 0. Számadatainkkal az $a)$ esetben $L-C{R}^2=0$ és az $AB$ pontok közötti feszültség bármely frekvenciánál 0, a $b)$ esetben $\omega =5000{\text{ s}}^{-1}$ és $U_x=0\mathrm{,}6U$.   Megadjuk az általános megoldás eredményét is: ${\displaystyle \begin{array}{c}\hfill {\displaystyle U_x=\frac{R^2-\left(L/C\right)}{\sqrt[]{\left[R^2+{\left(1/\omega C\right)}^2\right]\cdot \left[R^2+{\left(\omega L\right)}^2\right]}}\cdot U_0\text{sin}\left(\omega t+\phi \right)\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{tg}\phi =\frac{R\left[1/\left(\omega C\right)-\omega L\right]}{R^2+L/C}\mathrm{.}}\hfill \end{array}}$   A III. kísérleti forduló   A versenyzőknek adott olaj belső súrlódási együtthatóját kellett meghatározniuk adott berendezés felhasználásával, továbbá meg kellett vizsgálni, hogy ez az együttható független-e a sebességtől, és hogyan függ a hőmérséklettől.   Az 1982. évi tanulmányi verseny eredménye   A fizikából nem tagozatos tanulók versenyében:   1. díj:  Szállási Zoltán (Esztergom, Dobó Katalin Ginm. IV. o. t., tanára: Sípos Imre) 2. díj:  Károlyi Gyula (Budapest, Fazekas M. Gimn. IV. o. t., tanára: Horváth Gábor) 3. díj:  Náray Miklós (Budapest, I. István Gimn. III. o. t., tanára: Moór Ágnes)   A további helyezettek: 4. Kiss Péter (Zalaegerszeg, Zrínyi M. Gimn. IV. o. t., t.: Takács Jánosné), 5. Tóth Gábor (Budapest, Fazekas M. Gimn. III. o. t., t.: Horváth Gábor), 6. Fodor Zoltán (Budapest, Radnóti M. Gimn. III. o. t., t.: Tomcsányi Péter), 7. Csörgő Tamás (Gyöngyös, Berze N. J. Gimn. IV. o. t., t.: Kiss Lajos), 8. Marth Gábor (Budapest, Apáczai Cs. J. Gimn. III. o. t., t.: Holics László), 9. Tardos Gábor (Budapest, Berzsenyi D. Gimn. IV. o. t., t.: Apró Pál), 10. Pázmándi Ferenc (Debrecen, Tóth Á. Gimn. IV. o. t., t.: Kertész Béla). Két feladat megoldásáért elsőfokú dicséretet kapott egyenlő helyezésben 12 tanuló, egy feladat megoldásáért másodfokú dicséretet kapott egyenlő helyezésben 21 tanuló.   A fizikából tagozatos tanulók versenyében:   1. díj:  Földiák Péter (Budapest, Radnóti M. Gimn. IV. o. t., tanára: Rácz Mihály) 2. díj:  Tremmel János (Szombathely, Nagy Lajos Gimn. IV. o. t., tanára: Rozmán Gyula) 3. díj:  Járosi Péter (Dunaújváros, Münnich F. Gimn. IV. o. t., tanára: Kobzos Ferenc)   A további helyezettek: 4. Mádi Zoltán (Debrecen, Kossuth L. Gimn. IV. o. t., t.: Dudics Pál), 6. Bacsó Zsolt (Debrecen, Kossuth L. Gimn. IV. o. t., t.: Dudics Pál), 6. Oszlányi Gábor (Miskolc, Földes F. Gimn. IV. o. t., t.: Zámborszky Ferenc), 7. Jeney Tamás (Miskolc, Földes F. Gimn. IV. o. t., t.: Zámborszky Ferenc), 8. Nagy Ervin (Szombathely, Nagy Lajos Gimn. IV. o. t., t.: Karáth László), 9. Trefán György (Debrecen, Kossuth L. Gimn. IV. o. t., t.: Dudics Pál), 10. Molnár Ferenc(Dombóvár, Gőgös I. Gimn. IV. o. t., t.: Stettner Eleonóra). Két feladat megoldásáért elsőfokú dicséretet kapott egyenlő helyezésben 7 tanuló, egy feladat megoldásáért másodfokú dicséretet kapott egyenlő helyezésben 23 tanuló.