Kezdőlap


Cím:	1981. Beszámoló az Eötvös Loránd Fizikaversenyről
Szerző(k):	Károlyházy Frigyes , Vermes Miklós
Füzet:	1982/február, 81. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös, Loránd Fizikai Társulat 1981. október 17-én rendezte 58. versenyét Budapesten és 11 vidéki városban az azévben érettségizettek és középiskolások részére. A versenyzők 5 órai munkaidő alatt oldhatták meg a három feladatot. Bármely segédeszköz, használata meg volt engedve, beleértve a zsebszámítógépet is. A versenyen 209 dolgozatot adtak be. Ismertetjük a feladatokat és a verseny eredményét.

1. Az

1.

ábra szerinti vékony cső mindkét szára

L

hosszúságú. A zárt szárban és a vízszintes szárban elhelyezkedő higanyoszlop teljes hossza

L

. Az elzárt légoszlop hossza

l

. A szerkezetet az

O - O

tengely körül

ω

szögsebességgel forgatjuk. Állapítsuk meg a higanyoszlop elhelyezkedése és a szögsebesség közötti összefüggést ! Vizsgáljuk meg az egyensúlyi helyzetek stabilitását ! Számadatok: a külső légnyomás

p_{00} = 103 360 Pa

, a higany sűrűsége

ϱ = 13 600 {kg/m}^{3}

g = 10 {m/s}^{2}

L = 0, 1 m

l = 0, 025 m

Megoldás. Először kiszámítjuk az elzárt levegő

p_{0}

nyomását forgatás előtt. Ezt megkapjuk, ha a külső légnyomásból levonjuk a higanyoszlop hidrosztatikai nyomását:

\begin{matrix} p_{0} = p_{00} - (L - l) ϱ g . \end{matrix}

(1)

Vizsgáljuk azt az állapotot, amikor a higany részben még a bal oldali csőben is megvan, vagyis

l \leq x \leq L

, ahol

x

a higanyoszlop jobb oldali végének a forgástengelytől mért távolsága (2. ábra). A higany

x

adattal jellemzett állapotában az elzárt levegő nyomása

(p)

Boyle‐Mariotte törvénye szerint: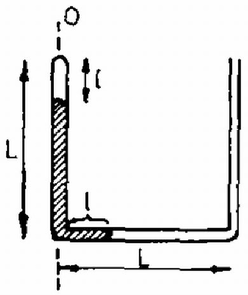

1. ábra

\begin{matrix} x p = p_{0} l, \end{matrix}

ebből (1) felhasználásával:

\begin{matrix} p = \frac{[p_{o o} - (L - l) ϱ g] l}{x} i \end{matrix}

(2)

A vízszintes szárban levő higany körpályán mozog, tehát a rá ható erők eredője (külső légnyomás mínusz az elzárt levegő nyomása és a függőleges szárban levő higany hidrosztatikai nyomása) egyenlő a centripetális erővel:

\begin{matrix} x ϱ ω^{2} \cdot \frac{x}{2} = p_{00} - p - (L - x) ϱ g . \end{matrix}

(3)

Miután a centripetális erő

r

-rel egyenes arányban növekszik, ezért a távolságok számtani középértékével számoltunk. Egyenletünkből (2)-vel az

ω

szögsebességet tudjuk kifejezni mint

x

függvényét:

\begin{matrix} ω = \sqrt[]{2 g [\frac{1}{x} + \frac{λ - L}{x^{2}} - \frac{l (l + λ - L)}{x^{2}}]} \end{matrix}

(3*)

ahol

\begin{matrix} λ = \frac{p_{00}}{g} \end{matrix}

(4)

célszerű rövidítő jelölés.

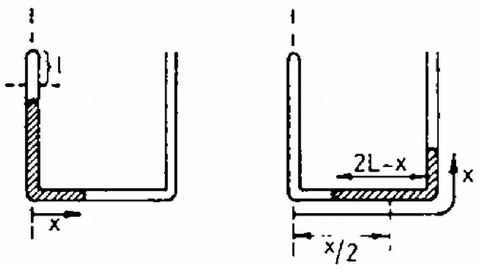2. ábra

(3) alatti képletünk addig érvényes, amíg a higany pontosan kitölti a cső alsó szárát. Ezután, amikor a higany már a jobb oldali csőbe is behatol, a hidrosztatikai nyomás előjele megfordul és az új egyenlet:

\begin{matrix} (2 L - x) ϱ ω^{2} \cdot \frac{x}{2} = p_{00} - \frac{[p_{00} - (L - l) ϱ g] l}{x} + (x - L) ϱ g . \end{matrix}

(

x

-szel itt is a 2. ábrán látható távolságot jelöltük.) Könnyen belátható, hogy a vízszintes szárban levő higany súlypontjának a tengelytől mért távolsága

x / 2

és a vízszintes szárban levő higanyoszlop hossza

2 L - x

. Az egyenlet megoldása

ω

-ra, ismét (4) alkalmazásával:

\begin{matrix} ω = \sqrt[]{2 g [\frac{1}{2 L - x} + \frac{λ - L}{(2 L - x) x} - \frac{l (l + λ - L)}{(2 L - x) x^{2}}]} . \end{matrix}

(5)

ω - x

függvény értékeit számadataink segítségével a (3*) és az (5) egyenlet alapján néhány pontban kiszámítottuk és a 3. ábrán ábrázoltuk.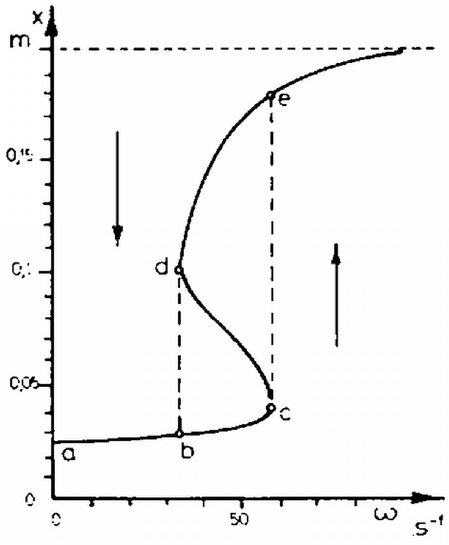

3. ábra

A görbe közepének furcsa menete miatt érdemes megoldásunkat kvalitatíve is átgondolni. Ha elkezdjük forgatni a csövet, létre kell hozni a vízszintes szárban levő higanyrészt körpályára kényszerítő centripetális erőt. Ha a higany kijjebb megy a vízszintes csőben, akkor ‐ mivel a körpálya sugarában befelé ható erő (a külső légnyomás) állandó,‐ sugárirányban a kifelé ható erő csökken, tehát megvan a körmozgást biztosító centripetális erő. Egyre nagyobb

ω

-hoz egyre nagyobb

x

tartozik mindaddig, amíg a bezárt levegő nyomásának és a függőleges szárban levő higany hidrosztatikus nyomásának csökkenése az egyre nagyobb centripetális erő növekedést szolgáltatni tudja. A feladatban megadott számadatok szerint ez

x = 0, 0378 m

-ig tart, amihez

ω = 58, 53 1 / s

tartozik. Növeljük tovább

ω

-t. Ekkor már a sugárirányban kifelé mutató erők csökkenése nem tudja fedezni a körpályán mozgáshoz szükséges centripetális erő növekedést, azaz a higany ,,átfut'' a másik csőszárba. Mint ahogy azt az (5) egyenletből láthatjuk, ebben a helyzetben már tetszőlegesen nagy

ω

-val forgathatjuk a csövet,

x

megváltozásával mindig biztosíthatjuk az egyensúlyi helyzetet. Fontos észrevenni, hogy

ω

folytonos növelésével a görbén a

c - d

szakasznak megfelelő egyensúlyi állapotok nem érhetők el. Ugyanilyen módon azt is beláthatjuk, hogy nagy

ω

-ról való fokozatos lassításnál sem jutunk rá a

c - d

állapotokra.
Ennek ellenére ezek olyan állapotok, amelyek, minthogy a (3) egyenlet jó megoldásai, egyensúlyi helyzetnek felelnek meg. Könnyű megmutatni, hogy el is érhetők. Pl. ha

ω

folytonos növelésével elértük

x = 0, 0378 m

-t, akkor nagyobb

x

értéknél úgy tudjuk csak biztosítani a centripetális erőt, ha

ω

-t csökkentjük. Mivel ez megtehető, a

c - d

szakasszal jelölt állapotok is megvalósíthatók. Azonban érezzük, hogy ezek az állapotok mégis mások, mint a többi görbeszakasszal megadottak. Ezt az érzésünket az állapot stabilitásának vizsgálata meg is erősíti. A stabilitáson azt értjük, hogy mi történik akkor, ha a testet valamely állapotában kis zavar éri. Nézzük meg először az

a - c

szakaszon a stabilitást. Legyen a test valamely

(x_{1}, ω_{1})

által jellemzett állapotban. Nevezzük (3) jobb oldalát

F (x)

-nek, ekkor

\begin{matrix} (1 / 2) x_{1}^{2} ϱ ω_{1}^{2} = F (x_{1}) . \end{matrix}

Valami kis zavar az adott

ω_{1}

szögsebesség mellett kimozdítja a higanyszálat egy

x'_{1} > x_{1}

helyre. Az

(x'_{1} ω_{1})

-gyel jellemzett körpályához tartozó centripetális erőnél azonban a higanyszálra ható tényleges erő nagyobb, hiszen

\begin{matrix} (1 / 2) ϱ x_{1}^{' 2} ω_{1}^{2} < (1 / 2) ϱ x_{1}^{' 2} ω_{1}^{' 2} = F (x'_{1}), \end{matrix}

mert nagyobb

x

-hez nagyobb

ω

tartozik az

a - c

szakaszon (

ω'_{1}

-vel az

x'_{1}

-höz tartozó egyensúlyi szögsebességet jelöltük). A nagyobb

F (x'_{1})

erő a higanyszálat visszanyomja eredeti helyére. Hasonló gondolatmenettel belátható az is, hogy

x'_{1} < x_{1}

esetén az

F (x'_{1})

kisebb lesz, mint a szükséges centripetális erő és a higanyszál a zavar elmúlta után megint visszamegy az eredeti helyére. Ezek az állapotok tehát stabilak. Nézzük meg, mi történik a

c - d

szakaszon. Épp a fordítottja mint előbb, hiszen itt nagyobb

x

-hez kisebb

ω

tartozik. Vagyis, ha a zavar az egyensúlyihoz képest nagyobb távolságra mozdítja ki a higanyszálat, akkora rá ható erő kisebb lesz, mint a szükséges centripetális erő, tehát még tovább mozdul az adott irányba, ekkor még kisebb lesz az erő stb. A higanyszál eredeti helyére nem tér vissza. Ha a zavar csökkenti

x

-et, akkor az

F (x)

nagyobb lesz, mint a szükséges centripetális erő és

x

-et tovább csökkenti stb. és így most sem tér vissza eredeti helyére. Ez a szakasz tehát instabil, gyakorlatilag igen nehezen megvalósítható, mert a legkisebb zavar esetén egy másik állapotba kerül a rendszer. Vegyük azt is észre, hogy az előbbieket nagyon szemléletesen úgy is elmondhatjuk, hogy ha a rendszer olyan nem egyensúlyi állapotba kerül, ami az egyensúlyi állapotot jelző görbétől jobbra van, akkor az

x

mindig nőni fog a zavar elmúlta után, míg, ha balra vagyunk az egyensúlyi görbétől, akkor az

x

csökkenni fog a zavar elmúlta után. Ennek segítségével is végiggondolhatjuk az egyensúlyi helyzetek stabilitását. Az

a - b - c

állapotok stabilak, mert ha a higany véletlenül kijjebb csúszna, akkor visszanyomódik a görbére, ha beljebb kerülne, akkor visszatolódna a görbén fekvő pont által jelzett állapotba. Ugyanez a helyzet a

d - e - \infty

darabon, ezek az állapotok is stabilak. A

c - d

darabon az egyensúlyi helyzet labilis, ha a higany befelé mozdulna el, akkor tovább mozog, amíg a

b - c

darabon egy stabilis egyensúlyi helyzetig el nem jut, ha kifelé mozdulna el, akkor tovább mozog, amíg a

d - e

darabon ér el stabilis egyensúlyi helyzetet. Érdekes a

c

és

d

pontokkal jelzett állapotok viselkedése. Ha

c

-ből befelé mozdul el a higany, akkor visszanyomódik

c

-be, ha kifelé csúszik, akkor eljut

e

-be. Ha

d

-ből befelé csúszik el, akkor eljut

b

-be, de kifelé elmozdulva visszatolódik

d

-be. (Hasonló esettel foglalkozik az 1981. évi Országos Középiskolai Tanulmányi Verseny I. fordulójának 4. feladata. KML. 63 (1981) 82. old.).

1 mól p_{1} = 40 {newton/cm}^{2}

V_{1} = 11, 2 {dm}^{3}

T_{1} = 546 K

adatokkal jellemzett héliumgázt úgy viszünk át a

p_{2} = 10 {newton/cm}^{2}

V_{2} = 44, 8 {dm}^{3}

T_{2} = 546 K

adatokkal jellemzett állapotba, hogy a

p - V

diagramon az állapotot jelző pont egy egyenesen mozogjon (4. ábra). Az állandó térfogat melletti fajhő

c_{V} = 12, 6 joule/(mól K)

.
a) Mennyi a folyamat közben elért

T_{m}

legmagasabb hőmérséklet ?
b) Mennyi az átlagos fajhő a

T_{1}

T_{m}

és a

T_{m} - T_{2}

szakaszon ? (Vermes Miklós)

\epsfbox{1982-02-84-1.eps} 4. ábra

Megoldás. a) Vegyük észre, hogy az 1. és 2. állapotot jelentő pontok szimmetrikusan feküsznek az első koordinátanegyedet felező

45^{\circ}

-os egyeneshez képest. Mivel

T_{1} = T_{2}

a két pont ugyanazon az izotermán fekszik. Mindebből következik, hogy a folyamat közben elért legmagasabb hőmérséklethez tartozó izoterma a két pontot összekötő egyenest a közepén érinti. A legmagasabb hőmérséklethez tartozó nyomások és térfogatok a kezdeti és végső állapothoz tartozó értékek számtani középértékei (5. ábra):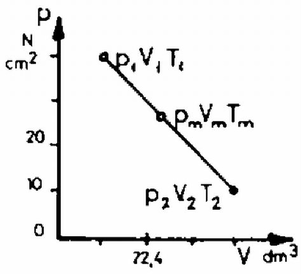

4. ábra

\begin{matrix} P_{m} = \frac{40 + 10}{2} {N/cm}^{2} = 25 {N/cm}^{2}, \\ V_{m} = \frac{11, 2 + 44, 8}{2} {dm}^{3} = 28 {dm}^{3} . \end{matrix}

Ezután az egyesített gáztörvényből meghatározhatjuk a legmagasabb hőmérsékletet:

\begin{matrix} \frac{40 {N/cm}^{2} \cdot 11, 2 {dm}^{3}}{546 K} = \frac{25 {N/m}^{2} \cdot 28 {dm}^{3}}{T_{m}} \end{matrix}

ahonnan

T_{m} = 853, 1 K = 580, 1^{\circ} C

.
b) Az I. főtétel szerint a gáz energiájának növekedése egyenlő a gázon végzett munkának és a gázzal közölt hőnek az összegével:

\begin{matrix} Δ E = Δ W + Δ Q . \end{matrix}

Átrendezve az egyenletet, megkapjuk a közölt hőt:

\begin{matrix} Δ Q = Δ Q - Δ W . \end{matrix}

(1)

Az átlagos fajhő pedig definíciója szerint:

\begin{matrix} C = \frac{Δ Q}{Δ W} . \end{matrix}

5. ábra

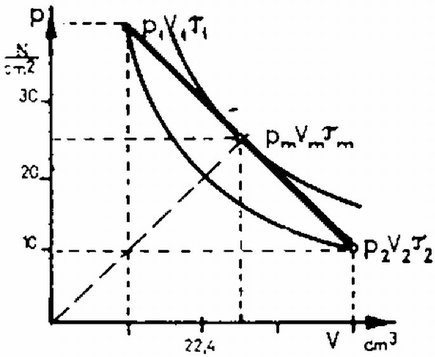Az 1. állapottól a maximális hőmérséklet elérésig tartó folyamatban a gáz energiájának növekedése:

\begin{matrix} Δ E_{1} = 1 mól \cdot c_{V} (T_{m} - T_{1}) = 3870 joule, \end{matrix}

(2)

mivel az ideális gáz belső energiája csak az abszolút hőmérséklettől függ.
A munkavégzést pedig, (amely negatív, mert a gáz végezte) a görbe alatti trapéz területe adja meg:

\begin{matrix} Δ W_{1} = - (1 / 2) (p_{1} + p_{m}) (V_{m} - V_{1}) = - 5460 joule . \end{matrix}

(3)

Behelyettesítve (2)-t és (3)-t (1)-be kapjuk, hogy

\begin{matrix} Δ Q_{1} = 3870 J - (- 5460 J) = 9330 joule \end{matrix}

A hőmérsékletváltozás

Δ T_{1} = T_{m} - T_{1} = 307, 1 K

.
Az adott folyamatra a

T_{1}

és

T_{m}

hőmérsékletek közti átlagos fajhő pedig

\begin{matrix} C_{1} = \frac{Δ Q_{1}}{Δ T_{1}} = 30, 39 joule/(mól K) . \end{matrix}

A maximumtól a 2-es állapotig tartó folyamatban a gáz energiája ugyanannyival csökken, mint amennyivel előbb nőtt, azaz

Δ E_{2} = - 3870 joule

. A munkavégzést az előbbihez hasonlóan számoljuk:

\begin{matrix} Δ W_{2} = - (1 / 2) (p_{m} + p_{1}) (V_{2} - V_{m}) = - 2940 joule . \end{matrix}

Ezeket az értékeket (1)-be beírva kapjuk, hogy

\begin{matrix} Δ Q_{2} = - 930 joule . \end{matrix}

Az átlagos fajhő most erre az adott folyamatra:

\begin{matrix} C_{2} = \frac{Δ Q_{2}}{Δ T_{2}} = 3, 03 joule/(mól K) . \end{matrix}

3. Egy transzformátornak

200, 300

és

400

menetes tekercsei vannak (6. ábra). Mely kapcsolásban lehet egy adott váltófeszültséget a lehető legnagyobb arányban erősíteni ?
(Károlyházy Frigyes)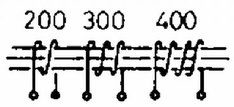

6. ábra

Megoldás. Mivel mindegyik tekercsen ugyanaz a fluxus halad át, a transzformátorból kivehető feszültség akkor a legnagyobb, ha a szekunder osztva primer menetszám ‐ hányados a legnagyobb. Ezt a hányadost és így a feszültségerősítést 4 esetre fogjuk kiszámolni (7. ábra).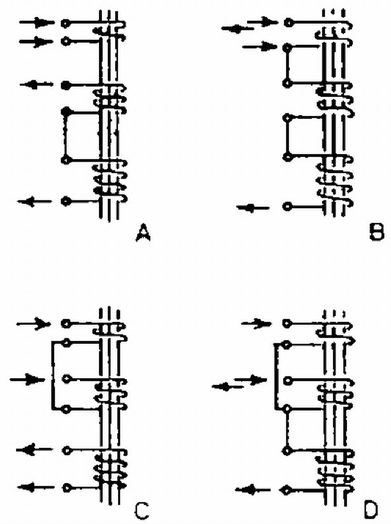

7. ábra

Ha a 200 menetes tekercset használjuk primernek és a sorba kapcsolt másik két tekercset szekundernek (7A ábra), akkor az erősítés

(300 + 400) : 200 = 3, 5

arányú. Nagyobb erősítést kapunk, ha autotranszformátort készítve a 200-as tekercset is hozzávesszük a szekunderhez (7B ábra), ekkor az erősítés

900 : 200 = 4, 5

arányú. Ha a 200-as és 300-as tekercseket ellentétesen kapcsoljuk, 100 menetes primer tekercsnek számítanak (7C ábra), és a 400 menetes szekunder tekercsen

4

-szeres feszültség keletkezik. A maximális kivehető feszültséget akkor kapjuk, ha az előbbi kapcsolást úgy módosítjuk, hogy a 400 menetes tekercset autotranszformátor módjára hozzákapcsoljuk a 300 menetes tekercshez (7D ábra). Ekkor a primer tekercsre (az ellentétesen kapcsolt 300 és 200 menetes tekercsek) adott feszültséget 7-szeresére erősíthetjük.

A verseny eredménye

I. díjat nyert Tokaji Zsolt honvéd, aki Szegeden a Ságvári Endre Gimnáziumban érettségizett, mint Kovács László tanítványa. II. díjat kaptak egyenlő helyezésben Mogyorósi András, a váci Sztáron Sándor Gimnázium IV. osztályos tanulója (tanára Skripeczky Gyula) és Petrovay Kristóf honvéd, aki a budapesti Ságvári Endre Gimnáziumban érettségizett mint Kulcsár András tanítványa. III. díjat kaptak egyenlő helyezésben Glück Ferenc az ELTE fizikus hallgatója,aki a budapesti Apáczai Csere János Gimnáziumban érettségízett mint Holics László tanítványa, Szállási Zoltán, az esztergomi Dobó Katalin Gimnázium IV. osztályos tanulója (tanára Sipos Imre) és Tóth Gábor, a budapesti Fazekas Mihály Gimnázium III. osztályos tanulója (tanára Horváth Gábor). Dícséretet kaptak egyenlő helyezésben Guba Kornél, a kazincbarcikai Ságvári Endre Gimnázium IV. osztályos tanulója (tanára Lehotczky Zoltán), Oszlányi Gábor, a miskolci Földes Ferenc Gimnázium IV. osztályos tanulója (tanára Zámborszky Ferenc) és Palasik Sándor honvéd, aki a bonyhádi Petőfi Sándor Gimnáziumban érettségizett mint Jurisits József tanítványa.