Cím: Bellmann feladata
Szerző(k):  Tóth Gábor 
Füzet: 1982/október, 53. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

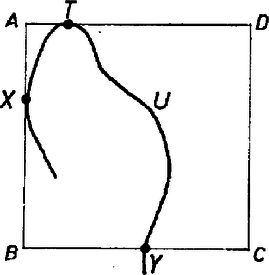
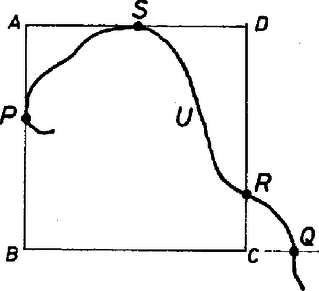
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az alábbi feladatot, mely R. Bellman amerikai matematikustól származik, D. O. Skljarszkij‐N. N. Csencov‐I M. Jaglom: Válogatott feladatok és tételek az elemi matematika köréből 2/2. Geometriai egyenlőtlenségek és szélsőérték feladatok c. gyűjteményben találtam (40. feladat):
Egy turista eltévedt az erdőben, ismeri az erdő alakját és méretét, de nem tudja, ő maga hol van. Tervezzük meg azt a minimális hosszúságú útvonalat, amelyet követve biztosan kijut az erdőből!
A feladatot az erdő alakjától függően több esetben vizsgáljuk. Az első kettőben a minimális hosszúságú kivezető utat a feladatgyűjtemény ismerteti.

 

1. Az erdő alakja kör. A megoldás: Haladjunk mindig egy irányban, így legfeljebb d egység megtétele után kijutunk az erdőből, ahol d a kör átmérője. Állítjuk, hogy ez a legrövidebb útvonal, amit követve feltétlenül kijut a turista az erdőből. Ugyanis tegyük fel, hogy létezik rövidebb útvonal. Helyezzük ennek középpontját (hosszának felezési pontját) a kör középpontjába, O-ba. Ha O-ból a végpontok valamelyike felé megyünk, nem juthatunk d/2-nél messzebbre, hiszen az útvonal hossza kisebb d-nél. Így az útvonal végéről indulva nem juthatunk ki az erdőből, tehát nem létezik d-nél rövidebb út (1. ábra).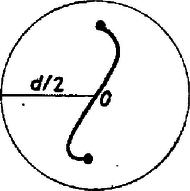
 

1. ábra
 

 

2. Az erdő félsík alakú, és tudjuk, hogy az erdő szélétől legfeljebb d távolságra vagyunk.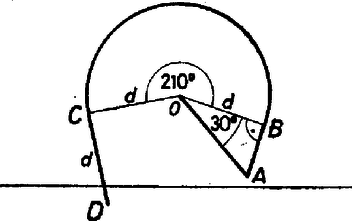
 

2. ábra
 

 

A 2. ábrán látható a legrövidebb kivezető útvonal. Az OABCD útvonal hossza kb. 6,40d, amiből OA=2d/3, AB=d/3, BC=7dπ/6 és CD=d. Ennek bizonyítása a fent említett feladatgyűjtemény szerint megtalálható J. R. Isbell, An optimal search pattern (Naveb. Res. Logist. Quart. 1957. 4. szám 357‐359. oldal) című cikkében.
 

3. Az erdő d szélességi sáv, illetve olyan d oldalú téglalap, melynek másik oldala legalább 2,278d.
Erre az esetre V. A. Zalgaller adott megoldást, de ezt nem sikerült megtalálnom.
 

4. Az erdő alakja négyzet. A minimális hosszúságú kivezető út d oldalú négyzet esetén a következő. Haladjunk egy kitűzött irányban; legfeljebb d2 utat (az átló hosszát) megtéve kijutunk az erdőből. Tegyük fel, hogy az U-val jelzett útvonal mindig kivezet a négyzet belsejéből. Megmutatjuk, hogy U hossza legalább d2.
 
3. ábra
 
4. ábra
 
5. ábra

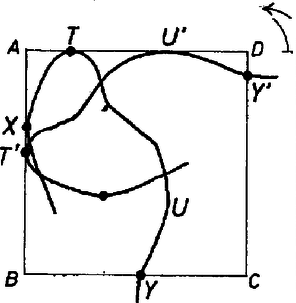
Ha U-t el tudjuk helyezni a négyzet belsejében úgy, hogy nem metszi annak egyik oldalát sem, akkor az útvonal rossz, hiszen nem vezet ki az erdőből. Jelöljük egy d élű négyzet csúcsait A, B, C, D-vel. Helyezzük el U-t az AB és AD félegyenesek által határolt síknegyedben úgy, hogy az AB, illetve AD félegyenesekkel legalább egy közös pontja legyen és teljes egészében ezeknek a félegyeneseknek a C csúcsot tartalmazó oldalára essen, azaz AB és AD az U támaszegyenesei legyenek. Az előbbiek miatt U metszi vagy BC-t, vagy DC-t, vagy mindkettőt (a "metszés'' azt jelenti, hogy van közös pontjuk), mert különben U-t az AC átlóval párhuzamosan megfelelően kis távolsággal eltolva, az útvonal teljes egészében a négyzet belsejébe kerülne. A szimmetria miatt feltehetjük, hogy U a BC-t metszi. Tehát U-nak van (legalább) egy X pontja az AB-n, egy Y pontja a BC-n és egy T pontja az AD oldalegyenesen (3. ábra).
Forgassuk U-t az óramutató járásával ellenkező irányban, és közben toljuk is el úgy, hogy AB és AD minden pillanatban támaszegyenes maradjon. U folytonosságából következik, hogy ez az " érintve‐forgó'' mozgás folyamatos, s így helyes a következő gondolatmenet: kezdetben U metszi BC-t. A forgatás minden pillanatában metszenie kell BC és DC közül legalább az egyiket. 90∘-os elforgatás után T az AB-re, Y a DC oldalegyenesre kerül, vagyis U metszi DC-t (4. ábra). Tehát volt olyan helyzete U-nak, amikor BC-t és DC-t is metszette. Ebben a helyzetben U-nak a négyzet minden oldalegyenesén van legalább egy pontja, hiszen AB és AD támaszegyenesek.
Jelöljük a négy metszéspontot P, Q, R, S-sel, amelyek rendre az AB, BC, DC, AD oldalegyeneseken vannak (lehetnek az oldalak meghosszabbításán is, 5. ábra). Vizsgáljuk meg, milyen sorrendben köti össze U ezeket a pontokat! Feltehetjük, hogy P az első. Ekkor lényegében két esetet különböztethetünk meg:
 

1. A második pont a szemközti oldalegyenesen van, azaz a második pont az R, továbbá feltehetjük, hogy a harmadik pont az S és az utolsó a Q (6. ábra). Ekkor PR≥AD és SQ≥AB, így U hossza ≥PR+RS+SQ≥AD+AB>BD.
 

2. A második pont az AB-vel szomszédos oldalegyenesen van, legyen ez például a Q. Most még két eset maradt:
 

2a) A harmadik pont az R és a negyedik az S. Az RDS és a PBQ derékszögű háromszögben RD≤RS és BQ≤PQ.
 

2b) A harmadik pont az S és a negyedik az R. Ekkor SD≤RS és BQ≤PQ, tehát a 2. esetben az út hossza csökken (legalábbis nem nő), ha P helyett B-ből megyünk Q-ba és S, illetve R helyett D-ben fejezzük be az utat. Így viszont a megtett út legalább 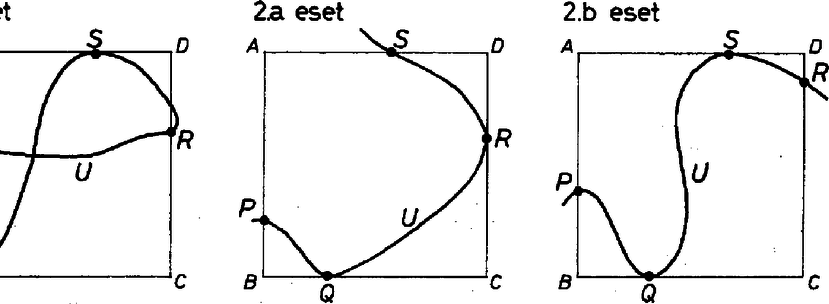BD, tehát U hossza ≥BD.
 

6. ábra
 

 
Minden esetben azt találtuk tehát, hogy U hossza nem kisebb az átló hosszánál, és ezt akartuk bizonyítani.
A bizonyítás általánosítható téglalapra bizonyos megkötéssel:
Ha feltesszük, hogy U-nak van olyan helyzete, melyben egyszerre metszi a távolabbi oldalpárt, akkor a bizonyítás közvetlenül átvihető, azaz U nem rövidebb a téglalap átlójánál. Ha viszont ez nem igaz, akkor U-t bármilyen irányba is fordítjuk, mindig a két távolabbi oldal közé esik, tehát U-nak mindig metszenie kell az egymáshoz közelebbi párhuzamos oldalakat. Legyen ezek távolsága h, ekkor a megoldás ugyanolyan, mint egy h szélességű sávban. Ez a következőt jelenti:
Egy téglalapban az oldalak arányától függően vagy az átló a megoldás, vagy megegyezik a sávra vonatkozó megoldással (határesetben a kettő azonos eredményt adhat). Sajnos nem ismerem Zalgaller megoldását, így nem tudom, hol a határ, de ez biztosan kisebb az általa megadott 2,278-nál és nagyobb, mint 3≈1,732. Tehát ha egy téglalapban az oldalak aránya nem nagyobb 3-nál, akkor a legjobb stratégia elindulni egy kiválasztott irányban, s így legfeljebb az átló megtétele után kijutunk az erdőből. Ilyen téglalap az összes páros oldalú szabályos sokszögben található, ha kiválasztunk négy megfelelő csúcsot. A szabályos hatszögben az oldalak aránya éppen 3.
 

5. Az erdő alakja páros oldalú szabályos sokszög. Az a stratégia, amelyik biztosan kivezet a sokszögből, kivezet a beleírt téglalapból is, így az út hossza legalább akkora, mint az átló, azaz a sokszög köré írt kör átmérője. Ez pedig megvalósítható, hiszen tetszőleges irányban haladva mindig kijutunk legfeljebb az átmérő megtétele után.
 

Összefoglalva: körből, téglalapból (az oldalak aránya ≤3), páros oldalú szabályos sokszögből akkor jutunk ki leghamarabb, ha elindulunk egy kiválasztott irányban. Így legfeljebb a köré írt kör átmérőjével egyenlő hosszú utat kell megtenni.
Megoldatlan a probléma szabályos háromszögre és általában páratlan oldalú szabályos sokszögekre. Érdekes, hogy egy szabályos háromszög alakú erdőből biztosan ki lehet jutni anélkül is, hogy az oldal hosszának megfelelő utat megtennénk. Több ilyen útvonalat is találtak, de a legrövidebb út még ismeretlen. A feladatot átvihetjük három dimenzióba is. Például melyik az a legrövidebb térgörbe, amelyik biztosan kivezet egy testből? Gömbre hasonló a megoldás, mint a síkban a körre, de kockára a bizonyítás már nem vihető át.
 

Tóth Gábor (Budapest, Fazekas M. Gyak. Gimn., IV. o. t.)