|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Problémák egy megoldott feladat kapcsán
Az 1981. évi Kürschák József matematikai tanulóverseny 2. feladata bástyák elhelyezésével kapcsolatos, egy, a szokásostól több vonatkozásban eltérő sakktáblán. A szokványos sakktábla mezőből áll, és ezek felváltva világosra és sötétre vannak festve. A feladat táblái továbbra is négyzet alakúak, de lehetnek nagyobb és kisebb méretűek is a sakkban használatosnál. Emellett nagyon sokszínűek: legfeljebb két-két mező lehet egyszínű. (A színek száma tehát legalább .) A színek váltakozására ezen túl nincs semmi megszorítás. A továbbiakban egy ilyen sakktáblát röviden színes sakktáblának fogunk nevezni.
Az említett feladat ekkor a II. megoldásban bizonyított, kissé általánosított formájában így fogalmazható:
Ha legalább , akkor bármely -es színes sakktáblán elhelyezhető bástya különböző színű mezőkre úgy, hogy semelyik kettő ne üthesse egymást. ( bástya ilyen elhelyezését röviden békés elhelyezésnek fogjuk nevezni.)
Az említett II. megoldásban azt bizonyítottuk -re vonatkozó teljes indukcióval, hogy ha legalább 4, és van egy mező, amelyikre nem szabad bástyát helyezni, akkor is lehetséges békés elhelyezés egy -es színes sakktáblán. A bizonyítás érdekessége, hogy a nehézséget a kezdő eset tárgyalása jelenti, tehát 4 bástya békés elhelyezése egy -es színes sakktáblán, ha egy mező tiltott. Annak bizonyítása, hogy ha valamilyen -ra -ás sakktáblára igaz az állítás, akkor igaz -es sakktáblára is, már szinte magától értetődő.
Az említett kezdő eset tárgyalásához be kellett látni és felhasználni azt is, hogy ha -as színes táblának egy mezőjére tilos bástyát tenni, akkor az 1. ábra szerint színezett táblán nem lehetséges békés bástyaelhelyezés ‐ és természetesen az ebből sorok vagy oszlopok felcserélésével vagy átlóra való tükrözéssel keletkező színezéseknél sem ‐, de egyéb színezésnél lehetséges.
Figyeljük meg, hogy ennél a színezésnél bármelyik -es résztáblának legalább az egyik átlójában különböző színű mezők állnak. Ezt az észrevételt a későbbiekben fel fogjuk használni.
Abból, hogy -es színes táblán egy tiltott mező esetén is van mindig békés bástyaelhelyezés, már az is könnyen belátható volt, hogy -nél nagyobb -re az -es színes sakktáblán akkor is lehetséges békés bástyaelhelyezés, ha van mező, amelyekre tilos bástyát tenni.
A következőkben azt vizsgálom, mennyire növelhető tovább azoknak a mezőknek a száma, amelyekről ki vannak tiltva a bástyák. Megmutatom a következőt:
TÉTEL. Ha és az -es sakktáblán megtiltjuk legfeljebb mezőre bástya elhelyezését ‐ azzal az egy kikötéssel, hogy nem lehet sem egy sor, sem egy oszlop minden mezeje tiltott ‐, akkor elhelyezhető a táblán bástya különböző színű mezőkre úgy, hogy semelyik kettő ne üthesse egymást.
A bizonyítás továbbra is teljes indukcióval fog történni, és továbbra is a kezdő eset tisztázása fog csak gondot okozni, nem is keveset, a tulajdonképpeni indukciós lépés jóformán semmit. A kezdő esetnél lépésről lépésre haladva a következőket fogjuk belátni:
a) -es színes táblán tiltott mező esetén is van békés bástyaelhelyezés.
b) -es színes táblán tiltott mező esetén csak akkor nincs békés bástyaelhelyezés, ha
a tiltott mezők egy sorban vagy egy oszlopban vannak, és ekkor is csak a 2. ábrán feltüntetett színezés esetén,
továbbá az ebből sorok, oszlopok cseréjével, valamelyik átlóra való tükrözéssel keletkező színezésnél,
végül az olyan színezésnél, amelyik a jobb felső -as résztáblának a jobbra felfelé haladó átlójára való tükrözésével keletkezik.
(Az üresen hagyott mezőkre nem kerülhet bástya békés elhelyezésnél, így azok színezhetők pl. egy-egy újabb színnel.)
c) Az -ös táblán még tiltott mező esetén is van békés bástyaelhelyezés, kivéve, ha egy sor vagy egy oszlop összes mezői a tiltottak.
A c) állítás a bizonyítandó tétel speciális esete -re (a ,,kezdő eset''). Ha ehelyett csak a)-t használjuk fel, akkor -es színes sakktáblán a tiltható mezők számát -ról csak -re tudjuk növelni. Így abban sem lehetünk biztosak, hogy ne lehetne a bizonyítandó mezőnél többre is megtiltani bástyák helyezését, ha növekszik. Az eddigiek után az látszik valószínűnek, hogy lehet.
Még azt sem láttuk be, hogy -ös táblán nem lehet -nél több mezőre megtiltani bástyák elhelyezését. Ehhez csak egy ellenpélda kell. Ez esetünkben azt jelenti, hogy úgy kell egy -ös tábláról mezőt elhagyni, és a maradókat kiszínezni, hogy egyik sornak vagy oszlopnak se legyen minden mezeje tiltott, a maradó mezőkön mégse legyen lehetséges békés bástyaelhelyezés. Próbáljon az olvasó ilyet csinálni, nem túl nehéz ! Ha ez sikerül, további meglepetésben is lesz része. Az ellenpélda átvihető tetszés szerinti mellett annak megmutatására, hogy az -es tábláról elhagyhatunk mezőt, és a megmaradókat kiszínezhetjük úgy ‐ egy színt legfeljebb két mező színezésére használva ‐, hogy a táblán ne létezzék békés bástyaelhelyezés. Ezek szerint bizonyítandó tételünk nem javítható tovább.
tiltott mezőnél kikötöttük, hogy ne legyen egy sor vagy egy oszlop minden mezeje tiltott. Tehetnénk hasonlóan további megszorításokat a tiltott mezők elhelyezésére és kérdezhetnénk, hogy így meddig növelhető a tiltott mezők száma, de ezzel egyre kevésbé érdekes kérdésekhez jutunk. Természetesen merül fel viszont a színezési feltétel gyengítése. Mit mondhatunk, ha csak azt kötjük ki, hogy ne legyen 3-nál több egyszínű mező; általában ha valamilyen pozitív egész számra azt tesszük fel, hogy nincs -nál több egyszínű mező ? Igaz-e, hogy minden pozitív egészhez van egy olyan korlát, hogy bármely -es táblán van békés bástyaelhelyezés, ha és a tábla színezésére az utoljára mondott feltétel teljesül ?
Az eredeti feladat annak bizonyítását kívánta, hogy -re mellett igenlő a válasz a kérdésre. -ra a probléma redukálása kisebb táblára még megy, csak valamilyen -ra kellene belátni az állítás helyességét. -nál nagyobb esetén viszont teljesen új gondolatok szükségesek a kérdés vizsgálatához.
Ha valakinek esetleg sakktáblával és bástyákkal fogalmazva túl játékosan, ,,a matematikához méltatlanul komolytalanul'' hangzik a probléma, azt megnyugtathatom, hogy könnyen átfogalmazható egy ,,komolyabb'', a matematikában ma már megszokott fogalomra: gráfokra vonatkozó problémává. A tábla sorait képviselje a pont, az oszlopait a , pont. Ekkor az -edik sor -edik mezejét a -t -vel összekötő vonallal ‐ éllel ‐ szemléltethetjük. Ezeket az éleket kell megszíneznünk úgy, hogy ne legyen -nél, ill. -nál, ill. -nál több egyszínű él, és a probléma az, ki lehet-e választani különböző színű élet úgy, hogy minden pont szerepeljen az élek végpontjai között. 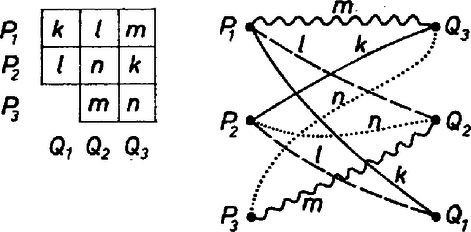 3. ábra
A bizonyítás vázlata, a redukciós lépés
Térjünk most vissza a esetre, a kimondott tétel bizonyítására. Mint említettem, a tábla nagyságára, pontosabban az egy oldal mentén sorakozó mezők számára vonatkozó teljes indukciót használunk. A bizonyítás itt is, mint a versenyfeladat II. megoldásában, megad egy eljárást a békés bástyaelhelyezés megkeresésére. Tulajdonképpen egy bástya elhelyezésével redukáljuk a feladatot lépésről lépésre egy 1-gyel rövidebb oldalú tábla esetére, amíg egy olyan táblához jutunk, amire már közvetlenül meg tudunk adni egy békés bástyaelhelyezést, vagy be tudjuk látni annak létezését.
A bizonyítandó tétel esetében az -ös tábla 5 tiltott mezővel lesz az ‐ mint említettem ‐, amire belátjuk békés bástyaelhelyezés létezését; továbbá belátjuk, hogy ha valamilyen -re minden -es színes táblán, tiltott mező esetén is lehetséges békés bástyaelhelyezés, akkor lehetséges az -es táblán is kizárt mező esetén.
Mondtam, hogy ez utóbbi lépés, a redukció kisebb méretű sakktáblára, egészen könnyű. Kezdjük ezzel, azután fogjuk megvizsgálni, hogyan helyezhetők el bástyák alkalmasan, kis táblákon.
Előrebocsátunk néhány megjegyzést, hogy a további gondolatmeneteket áttekinthetőbbé tegyük.
Fogjuk használni azt a sakkjátékból közhasznúvá vált kifejezést is, hogy egy bástya a vele egy sorban és egy oszlopban levő mezőket sakkban tartja. Ezt fogjuk használni a sakktábla egy-egy mezejével kapcsolatban is azokra a mezőkre, amelyeket a ráhelyezett bástya sakkban tart.
Szó volt már róla, hogy a tábla sorainak vagy oszlopainak felcserélése vagy tükrözése egy átlóra nem változtat a problémán, ez gyakran lehetővé teszi, hogy az éppen vizsgált mezők speciális elhelyezkedésére szorítkozzunk. Ilyenkor általában csak a speciális elhelyezést fogjuk megadni, az olvasóra bízva annak átgondolását, hogy az említett lépésekkel átrendezhető a tábla a mondott szerkezetűre.
Feltehetjük, és fel is fogjuk tenni, hogy az egyszínű mezők semmilyen színből nincsenek egy sorban, sem egy oszlopban, mert ha így helyezkednének el, akkor egy békés bástyaelhelyezésnél úgyis legfeljebb az egyiken állhatna bástya. Így nem változtatna a probléma megoldhatóságán, ha a két egyszínű mező egyikét átfestenénk egy, a táblán eddig még nem szereplő új színre.
Térjünk át ezután a redukciós lépésre. Ha egy bástyát elhelyeztünk, a mezejével egyszínű mezőre már nem tehetünk bástyát. Tehát 1-gyel növeljük a tiltott mezők számát, nekünk pedig 2-vel csökkenteni kellene azt, ha 1 mezővel rövidebb oldalú táblára térünk át. Úgy kell tehát elhelyeznünk a bástyát, hogy az eredetileg tiltott mezők közül legalább 3-at sakkban tartson. Ezt azonban könnyű elérni.
Tegyük tehát fel, hogy és -es táblákra igaz a TÉTEL. Vegyünk egy -es sakktáblát, amelyen tetszés szerint ki van jelölve mező, amelyekre tilos bástyát állítani, azzal az egy megszorítással, hogy nem lehet sem egy sorban, sem egy oszlopban tiltott mező; a többi mező pedig az előírás betartásával ki van színezve. Számoljuk meg mindegyik sorban és mindegyik oszlopban a tiltott mezők számát és válasszunk egy olyan sort vagy oszlopot, amelyikben ez a szám maximális. Feltehetjük, hogy az első sor ilyen. Feltétel szerint ebben a sorban is van olyan mező, amelyikre szabad bástyát állítani.
Ha az első sorban legalább 3 tiltott mező van, akkor tegyük az első bástyát bármelyik nem tiltott mezőre (4a ábra). Ennek a sorába és oszlopába nem helyezhető további bástya. A még kitöltendő -es táblán legfeljebb tiltott mező marad, de ehhez jöhet még egy mező, amelyik egyszínű azzal, amelyikre a bástyát helyeztük az első sorban. Így a megmaradó -es táblán legfeljebb mezőre nem helyezhetünk bástyát. Nem lehet ezek közül a tilos mezők közül sem egy sorban, sem egy oszlopban . Ha ugyanis volna, akkor azok közül legalább az eredetileg tiltott mezők közül volna, tehát legalább ennyi tiltott mező volna az eredeti táblából már elhagyott első sorban is. De ekkor az -es táblán legalább tiltott mező lett volna, nem csak . A maradó táblára tehát indukciós feltételünk szerint megoldható a probléma. 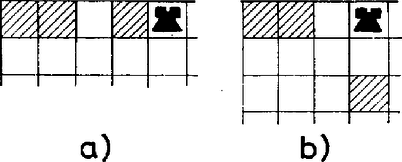 4. ábra
Egy 2 kizárt mezőt tartalmazó sor nem tiltott mezői közt van olyan, amelyiknek az oszlopában van kizárt mező (4b ábra), mert a kizárt mezők oszlopában most legfeljebb még kizárt mező lehet, és összesen 5-nél több van. Egy ilyen nem tiltott mezőre helyezve bástyát, az ismét legalább 3 tiltott mezőt tart sakkban, így a még kitöltendő -es táblán legfeljebb marad az eredetileg tiltott mezők közül, tehát az előbbi meggondolás most is alkalmazható. Az -es táblán tehát van békés bástyaelhelyezés, ha az -esen van, és ezt akartuk belátni.
-es sakktáblák és tiltott mezővel
Térjünk rá most már az a), b) és c) állítás bizonyítására. Ha -es táblán két tiltott mező van és azok nincsenek sem egy sorban, sem egy oszlopban, akkor az egyiket tartalmazó sor és a másikat tartalmazó oszlop közös mezejére lehet bástyát helyezni. Ha a tiltott mezők egy sorban vannak, akkor is van ebben a sorban olyan mező, amelyikre szabad bástyát helyezni. A kétféle lehetőséget összefoglalhatjuk úgy, hogy mondjuk, a legalsó sor és a bal szélső oszlop tartalmazza a két tiltott mezőt, de ezek közös mezeje nem tiltott.
Meggondolásunk érvényes lesz arra az esetre is, ha a sor és oszlop egyike egy, a másik két kizárt mezőt tartalmaz, de közös mezejük megengedett a bástyák számára.
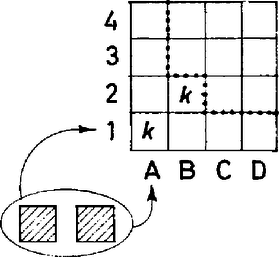 5. ábra
Ha, mondjuk, a B2 mező egyező színű A1-gyel, akkor B2-t a résztábla tiltott mezejének kell tekintenünk. Ekkor is elhelyezhető, mint említettük, 3 bástya a kívánt módon a résztáblán, kivéve az 1. ábra színezésének esetét és az abból a korábban említett átalakításokkal keletkezőket. Az ilyen színezések esetére kell tehát még megfelelő bástyaelhelyezést keresnünk.
Mind az A jelű oszlopban, mind az 1-es sorban van a sarokmezőn kívül is olyan, amelyikre lehet bástyát helyezni, sőt legalább az egyikben ‐ mondjuk, az 1-es sorban ‐ legalább két ilyen mező van. Ezeknek a színe különbözik a -as résztábla mezőinek színétől, mert az A1 mezővel egyszínű, a többi szín pedig a résztábla 2-2 mezején szerepel.
Tegyük az egyik bástyát az A oszlop egy, a sarokmezőtől különböző és nem tiltott mezejére. Az 1-es sorban van ettől különböző színű nem tiltott mező a sarokmezőn kívül. Egy ilyenre tegyük a második bástyát. A maradó két bástyát a -as résztábla egy -es részén kell elhelyeznünk. Minden ilyen résznek legalább az egyik átlója két különböző színű mezőből áll, tehát ebben az esetben is találtunk alkalmas bástyaelhelyezést.
A -es színes sakktáblán van tehát békés bástyaelhelyezés, akkor is, ha 2 kijelölt mezőre tilos bástyát helyezni, sőt még akkor is, ha 3 olyan tiltott mező van, melyek egyetlenegy bástyával sakkban tarthatók, de nincsenek mind egy sorban vagy egy oszlopban.
Legyen most a -es táblán 3 mező tiltva. Ha ezek pl. egy oszlopban vannak, akkor az oszlop egyetlen ,,szabad'' mezejére bástyát kell helyeznünk. Ha az ezután még szóba jövő -as résztábla tartalmaz az első bástya mezejével egyszínű mezőt, és a többi mezői az 1. ábra szerint vannak színezve, akkor a további 3 bástya nem helyezhető el megfelelő módon. Azt akarjuk még belátni, hogy minden ettől ,,lényegesen'' különböző esetben van békés bástyaelhelyezés.
Az eddigiek alapján az olyan eseteket kell már csak megvizsgálnunk, amelyekben a 3 tiltott mező nem tartható sakkban egyetlenegy bástyával. 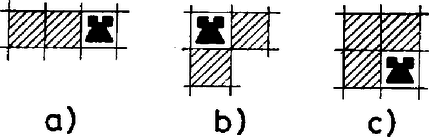 6. ábra
Két tiltott mezőt mindig sakkban lehet tartani egy bástyával, amint az a 6. ábráról könnyen leolvasható. Ha a harmadik mezőt úgy akarjuk elhelyezni, hogy ne tarthassa sakkban mind a hármat egyetlen bástya, akkor a tábla a 7a vagy 7b táblává rendezhető át (a színezésről még nem szólva).
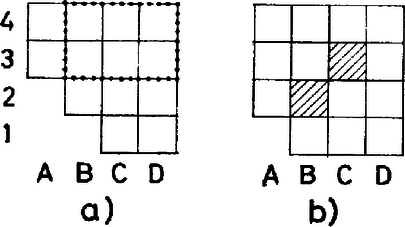 7. ábra
A táblán minden békés elhelyezésnek áll egy-egy bástyája az A oszlopban és az 1-es sorban. Mindegyikben 2 mezőre helyezhetünk bástyát, tehát ezt a 2 bástyát 4-féleképpen helyezhetjük el. A hátralevő 2 bástyát minden esetben egy -es résztáblán kell elhelyezni. Ez 2-féleképpen történhet, így a táblán 8-féle békés bástyaelhelyezés lehetséges.
Abból a 13 mezőből, amelyekre kerülhet bástya, 6 egyszínű mezőpár képezhető. Ezeket kellene úgy elhelyezni, hogy minden békés bástyaelhelyezés tartalmazzon egyszínű mezőpárt.
Egy mezőpárt, ha a mezők nincsenek sem egy sorban, sem egy oszlopban, a soraik és oszlopaik elhagyásával maradó -es résztábla kitöltésével egészíthetünk ki békés bástyaelhelyezéssé. Erre 2-féleképpen helyezhetők egymást nem ütő bástyák, ha nem tartalmaz tiltott mezőt; 1-féleképpen, ha 1 tiltott mezőt tartalmaz, vagy egyik átlója tiltott; különben nem helyezhetők. Akkor van tehát benne egy mezőpár 2 békés bástyaelhelyezésben, ha a rájuk helyezett bástyák mindegyik tiltott mezőt sakkban tartják, így esetünkben A1-et is. Ehhez a pár egyik mezejének vagy az A oszlopban vagy az 1-es sorban kell lennie, és a másiknak sakkban kell tartania a harmadik tiltott mezőt. A mezőpár így vagy a bal felső vagy a jobb alsó -es résztábla egyik átlója, vagy egy A oszlopbeli és egy 1-es sorbeli mezőből áll.
Figyeljük meg továbbá, hogy a 7a ábrán szaggatottan bekerített téglalap minden békés bástyaelhelyezésnek 1 bástyáját tartalmazza csak, mert a 3-as és 4-es sor bástyái közül az egyiknek az A oszlopban kell lennie. Ugyanez a helyzet a téglalap A1-en átmenő átlóra vett tükörképével is. Feltehetjük tehát, hogy egyik téglalapban sincs két egyszínű mező, mert ha volna, átfesthetnénk őket két új színre anélkül, hogy ez változtatna a békés bástyaelhelyezéseken.
A mindkét téglalapban benne levő 4 mező így különböző színű, és az ezekkel egyező színű mezők, ha vannak, csak az 1-es sor, az A oszlop mezői és B2 közül kerülhetnek ki.
Ahhoz, hogy a 8 lehetséges békés bástyaelhelyezés mindegyikét kizárjuk, legalább 2 egyszínű mezőpárnak 2-2 békés elhelyezést kell kizárnia. Ezek közt nem lehet olyan pár, amelyik egy 1-es sorbeli és egy A oszlopbeli mezőből áll, mert ez már lefoglal kettőt a jobb felső 4 mező párjaiként szóba jövő 5 mezőből. Így legfeljebb 3 mező számára marad pár. Ezekhez jöhet még 2 olyan pár, amelyik egy B oszlopbeli és egy 2-es sorbeli mezőből áll. Az ilyenek is csak 1-1 békés bástyaelhelyezésben lehetnek benne, mert nem tartják sakkban A1-et. Az összes egyszínű mezőpár tehát békés bástyaelhelyezésben fordulhat elő. Az sem javít a helyzeten, ha szaporítjuk az olyan egyszínű mezőpárok számát, amelyek 2 békés bástyaelhelyezést zárnak ki, mert annyival kevesebb jobb felső sarokbeli mezőnek jut pár, és így nem növekszik a kizárt békés elhelyezések száma.
A bal felső -es résztábla átlói a jobb alsó átlóival alkotnak békés bástyaelhelyezést, összesen 4-et. Ha mindegyik négyzet egyik átlója áll csak egyszínű mezőkből, akkor van egy olyan békés bástyaelhelyezés, amelyik mindkét mezőpárt tartalmazza, s így csak 3 békés bástyaelhelyezést zár ki a két mezőpár valamelyike.
Akkor zárja csak ki mind a 4 lehetséges békés bástyaelhelyezést egyszínű mezőpár, ha az egyik négyzet átlói állnak 2-2 egyszínű mezőből. Ekkor a jobb felső négyzet mezői közül ismét legfeljebb 3-nak jut azonos színű pár, viszont Bx, X2 típusú mezőpár most nem alkotható, mert a B oszlopnak vagy a 2-es sornak két erre alkalmas mezejét már felhasználtuk. Így ismét legfeljebb 7 békés bástyaelhelyezést zár ki egyszínű mezőpár. A 7a tábla esetén tehát mindig van békés bástyaelhelyezés. 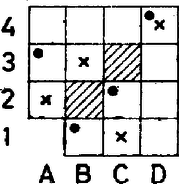 8. ábra
Ha a résztábla egyik mezeje D4-gyel egyező színű, akkor a résztáblából már 3 mezőt felhasználtunk, így csak 3 marad olyan mezőpárok kialakításához, amelyek 2-2 békés bástyaelhelyezést zárnak ki; eddig 1-et hoztunk létre, az 5-öt tehát nem értük el.
Ha viszont nincs D4-gyel egyező színű mező, akkor 2 olyan egyszínű mezőpárra van szükség, amelyik a bal alsó -as résztáblában van. Így ugyan 2 olyan pár keletkezett, amelyek 2-2 békés bástyaelhelyezést hiúsítanak meg, de már csak további 2 képzésére áll mező rendelkezésre a -as résztáblán, az 5 tehát így sem érhető el. Azt nyertük, hogy a 7b ábra tábláján is van békés táblaelhelyezés, bárhogy színezzük is a mezőket. Ezzel a b) állítás helyességét is beláttuk.
Az -ös táblák vizsgálata
Vizsgáljuk végül az -ös táblát 5 tiltott mezővel. Ezek feltétel szerint nem lehetnek mind egy sorban, sem egy oszlopban. Ha csupa különböző sorban és oszlopban vannak, akkor feltehetjük, hogy az egyik átlóban vannak (9. ábra).
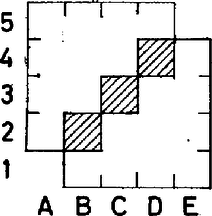 9. ábra
Számláljuk meg az A oszlop egyes mezőit tartalmazó lehetséges békés bástyaelhelyezéseket. Egy-egy ilyen mezőre bástyát téve, az 2 tiltott mezőt tart sakkban. A visszamaradó -es résztáblán tehát 3 tiltott mező van, csupa különböző sorban és oszlopban. Az előző részben beláttuk, hogy egy ilyen táblán 11 békés bástyaelhelyezés lehetséges (ha a színezés is megengedi). -ös táblánkon tehát 44-féle békés bástyaelhelyezés lehetséges.
Egy mezőpárt nézve, a ráhelyezett bástyák legfeljebb 4 tiltott mezőt tarthatnak sakkban, így a soraik és oszlopaik elhagyása után maradó -as tábla tartalmaz legalább egy tiltott mezőt. Ekkor azonban legfeljebb 4-féle békés bástyaelhelyezés fordulhat elő a résztáblán.
A bástyák elhelyezésére 20 mező áll rendelkezésre, ezekből 10 egyszínű pár képezhető. Így az elmondottak szerint legfeljebb 40 békés bástyaelhelyezést zárhat ki egyszínű mezőpár. Van tehát olyan bástyaelhelyezés is, amelyikben a bástyák csupa különböző színű mezőn állnak, és nem üthetik egymást.
Ha van olyan mező, amelyikre helyezett bástya legalább 4 tiltott mezőt sakkban tart, akkor ennek a sorát és oszlopát elhagyva a maradó -es táblán 1 eredetileg tiltott mező marad, továbbá arra a mezőre sem helyezhetünk bástyát, amelyik egyező színű az elhelyezett bástya mezejével, tehát legfeljebb 2 mező tiltott. Láttuk azonban, hogy az ilyen táblákra megoldható a probléma.
Ha van 3 tiltott mező egy vonalban, mondjuk az A oszlop 1-es, 2-es és 3-as mezeje tiltott, akkor amennyiben a 4-es vagy 5-ös sorban van tiltott mező, úgy sakkban tartható 4 tiltott mező 1 bástyával. Ha ez nem áll fenn, akkor is legfeljebb úgy juthatunk olyan -es táblához, amelyiken nincs békés bástyaelhelyezés, ha a további 2 tiltott mező egy sorban vagy egy oszlopban van, ami alkalmas sor- és oszlopcserékkel, ha kell, a 10. ábra a) vagy b) táblájába vihető át. 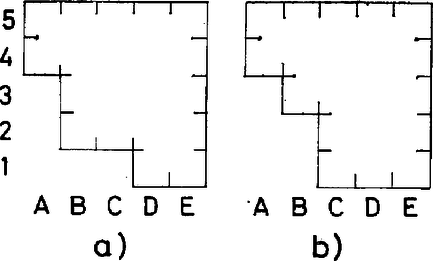 10. ábra
A 10.b. ábra esetében hasonlóan csak azt az esetet kell megvizsgálnunk, amikor az A oszlopbeli mezőkkel vannak egyező színű mezők, éspedig a B oszlopban. Az egyikkel egyező színű mező a 4-es vagy 5-ös sorban kell hogy legyen. Feltehetjük, hogy A4 és B5 egyező színű. Ekkor A5-tel B3, vagy B4 egyező színű (11. ábra). 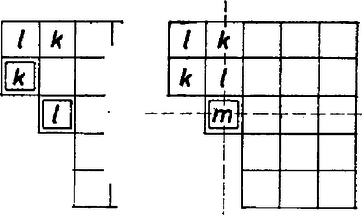 11. ábra
Hátra van még az az eset, amikor van 2 tiltott mező egy vonalban ‐ mondjuk A1-re és A2-re nem helyezhető bástya ‐, de nincs semelyik sorban vagy oszlopban 2-nél több tiltott mező. Ekkor az 1-es és 2-es sorban csak 1-1 további tiltott mező lehet, tehát kell tiltott mezőnek lennie a további sorok valamelyikében is, így sakkban lehet tartani legalább 3 tiltott mezőt, alkalmasan helyezve el egy bástyát az A oszlopban. Ezzel ismét csak akkor kaphatunk olyan -es táblát, amelyikre nem oldható meg a probléma, ha van 2 további tiltott mező egy sorban vagy oszlopban és ezekhez csatlakozik még a felhasználttal egyező színű mező.
Nem lehet 2 további tiltott mező egy sorban, mert az 1-es és 2-es sorban csak 1-1 további lehet az A oszlopbelin kívül, ha pedig a további sorok valamelyikében lenne 2, akkor 4 tiltott mezőt is sakkban lehetne tartani, alkalmasan helyezve el egy bástyát az A oszlopban.
Ha egy további oszlopban ‐ mondjuk B-ben ‐ van 2 tiltott mező, akkor az ötödik tiltott mező nem lehet ezekkel sem egy sorban, sem egy oszlopban. Ha emellett a B oszlopban levő tiltott mezők közül valamelyik a fölső 3 sor valamelyikébe esik, akkor ennek (vagy az egyik ilyennek) a sorába téve egy bástyát, az A oszlopban (12. ábra) olyan -es tábla marad vissza, amelyikben legfeljebb 3 tiltott mező lehet, de nem lehet mind sem egy sorban, sem egy oszlopban. Ezen ismét van békés bástyaelhelyezés. 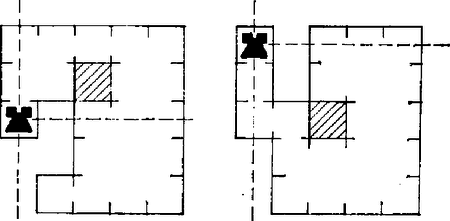 12. ábra  13. ábra
 14. ábra
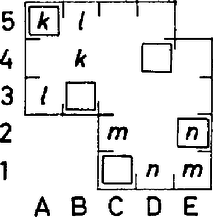
Ha az A5-tel és B5-tel egyező színű mezők nincsenek egy sorban, mondjuk B4, ill. A3 ez a két mező, akkor ezekre helyezve egy-egy bástyát, egy -as résztábla marad vissza 1 tiltott mezővel, mert az elhelyezett bástyák mindegyike sakkban tartja a másik mezejével egyszínű mezőt (14. ábra). Ha ez a -as résztábla az 1. ábra szerint van színezve, akkor merül fel probléma. Ez esetben az E oszlop mezőivel egyszínű mezők nem lehetnek egy oszlopban, mert különben volna a -as résztáblának olyan -es része, amelyiknek az átlói 2-2 egyszínű mezőből állnának, az 1. ábrán pedig ilyen nincs. Mondjuk, E1 és C2, továbbá E2 és D1 egyszínűek.
A -as résztábla minden mezővel együtt tartalmaz egy azzal egyszínű mezőt is. Így a C1-gyel és a D2-vel egyszínű mezők az 5-ös sorban vannak. Helyezzünk bástyát A5-re és B3-ra. Az utóbbinak a színe C4 és D4 közül legalább az egyikétől különbözik, mondjuk az utóbbiétól. Ekkor A5, B3, C1, D4, E2 egy békés bástyaelhelyezés.
Természetesen ugyanez a meggondolás érvényes a sorok és oszlopok szerepének cseréjével, ha az E1 és E2-vel egyszínű mezők a 2-es, ill. 1-es sorban, de nem ugyanabban az oszlopban vannak.
Legyen végül az A5, B5, E1, E2-vel egyszínű mező rendre B4, A4, D2, ill. D1 (15. ábra).
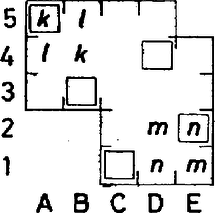 15. ábra
A D4 mező színe egy ezekétől különböző szín, és különbözik A3 és B3, továbbá C2 és C1 közül legalább az egyik-egyiknek a színétől, mondjuk, mindkét esetben különbözik az utóbbiétól. Ekkor A5, B3, C1, D4, E2 ismét békés bástyaelhelyezést tesz lehetővé.
Ezzel beláttuk, hogy ha -ös táblán bárhogy is helyezünk el 5 tiltott mezőt (csak nem mindet egy sorba vagy egy oszlopba), akkor mindig található békés bástyaelhelyezés, és ezzel mindegyik állításunk bizonyítást nyert.
Megoldását lásd e Lapok 1982 évi februári számában, 54-58. oldal |
 PDF | MathML
PDF | MathML