Kezdőlap


Cím:	Hány nevezetes pontja legyen a háromszögnek? (Fordította Láng Hugó)
Szerző(k):	Bauer, Hermann
Füzet:	1982/április, 145 - 152. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Hány nevezetes pontja legyen a háromszögnek?¹

(Fordította Láng Hugó)

1. A nevezetes pontok száma és tulajdonságaik

A háromszögben a súlypontot

(S)

, a körülírt kör középpontját

(K)

, a beírt kör középpontját

(O)

és a magasságpontot

(M)

szokás nevezetes pontnak mondani. Ezek mindegyike három-három nevezetes egyenes metszéspontja:

S

a súlyvonalak,

K

az oldalfelező merőlegesek,

O

a szögfelezők,

M

pedig a magasságvonalak közös pontja. Joggal kérdezhető azonban, miért csak ezeket mondjuk nevezetesnek, nem lehet-e valamilyen természetes módon további pontokat közéjük sorolni ?
Vegyük először szemügyre a háromszög nevezetes egyeneseit, és próbáljuk meg rendszerezni a tulajdonságaikat.¹ Négy nevezetes tulajdonságot találunk, ezek mind az egyeneseknek a háromszög valamelyik csúcsához vagy a vele szemközt levő oldalához való viszonyát határozzák meg:²

T_{1}

‐ az egyenes átmegy a csúcson;

T_{2}^{*}

‐ az egyenes felezi a csúcsnál levő szöget;³

T_{3}

‐ az egyenes merőleges a szemközti oldalra;

T_{4}

‐ az egyenes felezi a szemközti oldalt.

Mindegyik nevezetes vonal ezek közül kettővel rendelkezik: a súlyvonal

T_{1}

-gyel és

T_{4}

-gyel, az oldalfelező merőleges

T_{3}

-mal és

T_{4}

-gyel, a szögfelező

T_{1}

-gyel és

T_{2}^{*}

-gal, a magasságvonal

T_{1}

-gyel és

T_{3}

-mal. De kimerítettük-e ezzel az összes lehetőséget? A négy tulajdonságból pusztán kombinatorikailag hat pár képezhető:

T_{1} T_{2}^{*}

T_{1} T_{3}

T_{1} T_{4}

T_{2}^{*} T_{3}

T_{2}^{*} T_{4}

T_{3} T_{4}

. A baj csak az, hogy a hiányzó

T_{2}^{*} T_{3}

T_{2}^{*} T_{4}

párok valójában három tulajdonságot jelentenek:

T_{2}^{*}

és

T_{3}

együtt azt kívánná, hogy az egyenes menjen át egy csúcson, felezze az ott levő szöget, és legyen merőleges a szemközti oldalra,

T_{2}^{*}

és

T_{4}

pedig azt, hogy az egyenes menjen át egy csúcson, felezze az ott levő szöget, és felezze a szemközti oldalt. Azon nem tudunk segíteni, hogy egy egyenes általában vagy felezi a háromszög két oldala közti szöget, vagy merőleges a harmadik oldalra. De ha nem tesszük bele

T_{2}

-be

T_{1}

-et, akkor

T_{2}

és

T_{4}

már előfordulhat együtt. Legyen tehát

T_{2}

a következő tulajdonság:

T_{2}

‐ az egyenes ugyanakkora szöget zár be a csúcson átmenő oldalakkal.

T_{2}

tehát önmagában csak azt követeli meg, hogy az egyenes párhuzamos legyen a szögfelezővel és csak

T_{1}

-gyel együtt jelenti azt, hogy azonos is legyen vele.

T_{2}

és

T_{4}

így már nem zárják ki egymást. Együttes előfordulásuk egy ötödik nevezetes vonal bevezetését teszi lehetővé : ez az az egyenes, amelyik egyállású a szokásos szögfelezővel és illeszkedik a szemközti oldal felezőpontjára. Nevezzük ezt az egyenest oldalfelező szögfelezőnek. Látni fogjuk, hogy az általános háromszög oldalfelező szögfelezői egy ponton mennek át (1. tétel), ezt a pontot

F

-fel jelöljük, magukat az oldalfelező szögfelezőket pedig

f_{a}

-val,

f_{b}

-vel,

f_{c}

-vel.
Állítsuk párba a fenti tulajdonságokat úgy, hogy

T_{1}

-nek

T_{4}

T_{2}

-nek

T_{3}

legyen a párja! Ezáltal az öt nevezetes vonal is párba állítható:

\begin{matrix} T_{1} T_{2}‐ szögfelező & párja & T_{4} T_{3}‐ oldalfelező merőleges \\ T_{1} T_{3}‐ magasságvonal & párja & T_{4} T_{2}‐ oldalfelező szögfelező \\ T_{1} T_{4}‐ súlyvonal & párja & T_{1} T_{4}‐ súlyvonal \\ T_{2} T_{4}‐ oldalfelező szögfelező & párja & T_{3} T_{1}‐ magasságvonal \\ T_{3} T_{4}‐ oldalfelező merőleges & párja & T_{2} T_{1}‐ szögfelező \end{matrix}

T_{2} T_{3}

pár továbbra sem valósítható meg, itt lyuk marad a rendszerben. De mégis olyan rend keletkezett, amely korábban nem volt meg.

T_{1}

és

T_{4}

háromszor,

T_{2}

és

T_{3}

kétszer fordul elő, emiatt az ötféle egyenes közül egy-egy csúcson három megy át és ugyancsak három felez egy-egy oldalt. Két nevezetes egyenes merőleges egy-egy oldalra és ugyancsak kettő zár be két-két oldallal egyenlő szögeket. Rendszerünkben egyfajta megfeleltetés, dualitás mutatkozik

T_{1}

és

T_{4}

, valamint

T_{2}

és

T_{3}

között. Ha minden

T_{1}

-et és

T_{4}

-et, illetve

T_{2}

-t és

T_{3}

-at felcserélünk egymással a táblázatban, akkor minden egyenes átmegy az ebben értelemben vett duálisába. A szögfelezőnek így az oldalfelező merőleges felel meg, a magasságvonalnak az oldalfelező szögfelező, és megfordítva. A súlyvonal duálisa önmaga. Látni fogjuk, hogy ez a kapcsolat még további összefüggéseket rejt magában. (Meg kell azonban jegyezni, hogy itt szó sincs a projektív geometriában használatos dualitásról, hiszen ott minden tételnek megadható a párja; de azért a fenti megfeleltetés is termékeny ötletekre vezethet.)

2. Az oldalfelező szögfelezők tulajdonságai és a metszéspontjuk létezése

1. tétel. Bármely háromszög három oldalfelező szögfelezője egy pontban metszi egymást.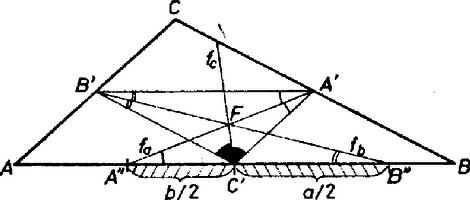

1. ábra

Bizonyítás. Az

A B C

háromszög oldalfelező szögfelezői ugyanis az

A' B' C'

középháromszög szögfelezői (1. ábra).

2. tétel. Az oldalfelező szögfelezők a háromszög mindhárom oldalát metszik. Egy oldalon az oldalfelező ponttól a másik két metszéspontig terjedő szakaszok rendre egyenlőek a másik két oldal felével.

Bizonyítás. Az oldalfelező szögfelezők metszik a középháromszög oldalait, tehát metszik az eredeti háromszög oldalait is. Tekintsük az

A B

oldalt, és jelöljük

f_{a}

f_{b}

A B

-vel alkotott metszéspontját

A''

-vel,

B''

-vel. Mivel

f_{a}

egyenlő szöget zár be

A B

-vel és

A' C'

-vel, az

A' A'' C'

háromszög egyenlő szárú,

A'' C' = A' C' = b / 2

. Hasonlóan kapjuk, hogy

B'' C' = B' C' = a / 2

Megjegyzések. a) Az 1. ábrán

a < c

b < c

, így

A''

A C'

B''

B C'

szakaszon van, és például

A A'' = (c - b) / 2

. Általában

\begin{matrix} A A'' = \frac{| c - b |}{2} . \end{matrix}

b) A külső szögfelezőkhöz hasonlóan beszélhetünk oldalfelező külső szögfelezőkről is, ezek ugyanúgy felezik az oldalakat, mint az oldalfelező szögfelezők, de a külső szögfelezőkkel párhuzamosak.

^{*}

¹ Könnyen látható, hogy a 2. tétel az oldalfelező külső szögfelezőkre is igaz, csak a metszéspontok rendre az oldalfelező pontok másik oldalán keletkeznek, mint az oldalfelező belső szögfelezők metszéspontjai.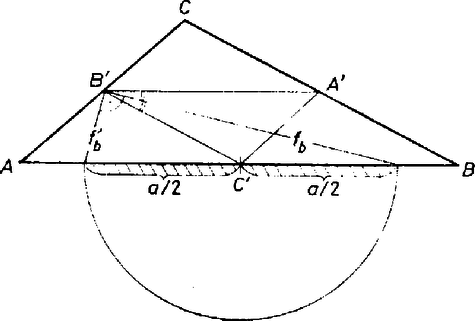

2. ábra

c) Az egyik oldal felezőpontján átmenő oldalfelező belső szögfelező és oldalfelező külső szögfelező merőlegesek egymásra, és valamelyik másik oldalt annak felezőpontjára szimmetrikus pontokban metszik. A két metszéspont távolsága egyenlő a harmadik oldal hosszával (2. ábra). Ennek alapján könnyen megszerkeszthetjük az oldalfelező szögfelezőket, például a 2. ábrán a

C'

körüli

a / 2

sugarú kör metszi ki az

A B

egyenesből a

B'

-n átmenő oldalfelező szögfelezők metszéspontjait.

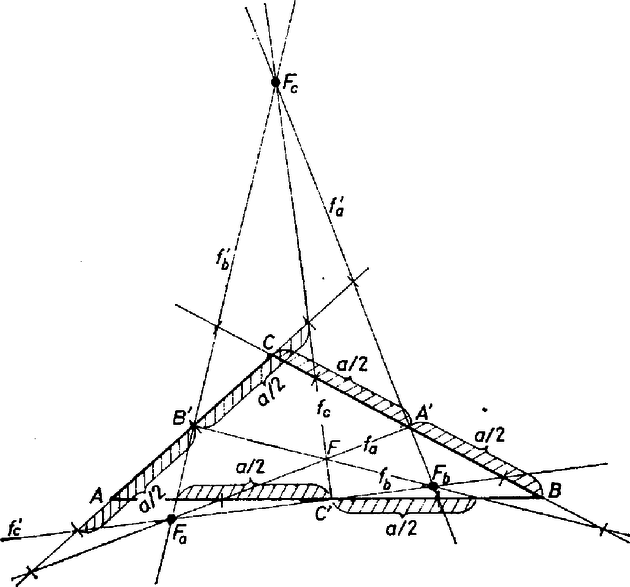3. ábra

A 3. ábrán berajzoltuk az

A B C

háromszögbe mind a hat oldalfelező szögfelezőt. Három újabb metszéspont keletkezik, ezeket

F_{a}

-val,

F_{b}

-vel,

F_{c}

-vel jelöljük. Ezek a középháromszöget kívülről érintő körök középpontjai, és

F

F_{a} F_{b} F_{c}

háromszög magasságpontja. A jobb tájékozódás kedvéért külön megjelöltük az ábrán az

a / 2

nagyságú szakaszokat.

3. tétel. Egy háromszögben az

O

S

F

pontok egy egyenesre illeszkednek, és

O S = 2 F S

(4. ábra).

Bizonyítás. Az

A' B' C'

középháromszög középpontosan hasonló az

A B C

háromszöghöz, a hasonlóság aránya

1 : (- 2)

, középpontja

S

. Emiatt az

A B C

-be írt kör

O

középpontját

F

-fel összekötő egyenes illeszkedik

S

-re, és

S

O F

szakaszt

2 : 1

arányban osztja.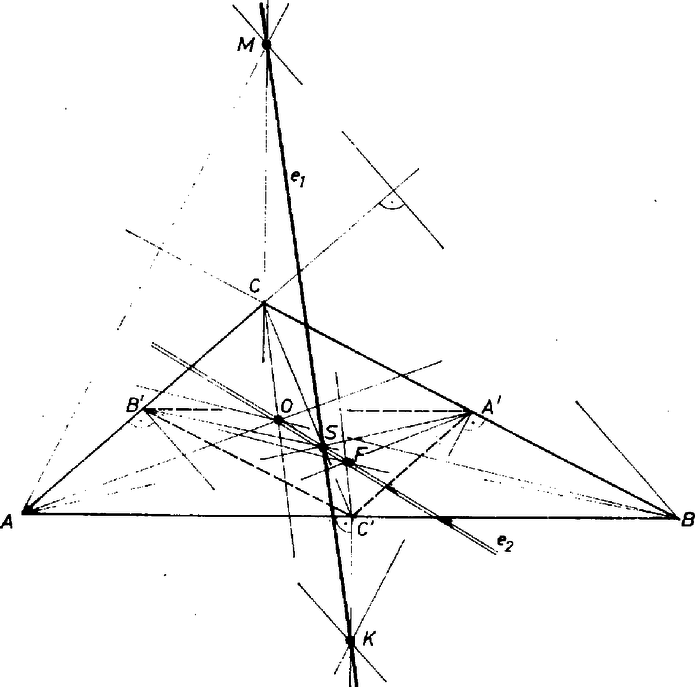

4. ábra

A kapott egyenest az

A B C

háromszög második Euler egyenesének nevezzük. (Az első Euler egyenes a

K

S

M

pontokon megy át, és mint tudjuk,

M S = 2 K S

.)
Megjegyzés. Az

O M F K

négyszög átlói a háromszög Euler egyenesei, metszéspontjuk

S

és ez az átlókat

2 : 1

arányban osztja. Emiatt

O M ∥ F K

és

O M = 2 F K

(4. ábra).

4. tétel. Tükrözzük

O

-t

F

-re, és jelöljük a kapott pontot

G

-vel. Ez a

G

pont rajta van a második Euler egyenesen, és a beírt kör középpontja abban az

A'' B'' C''

háromszögben, amelyben

A B C

a középháromszög (5. ábra).

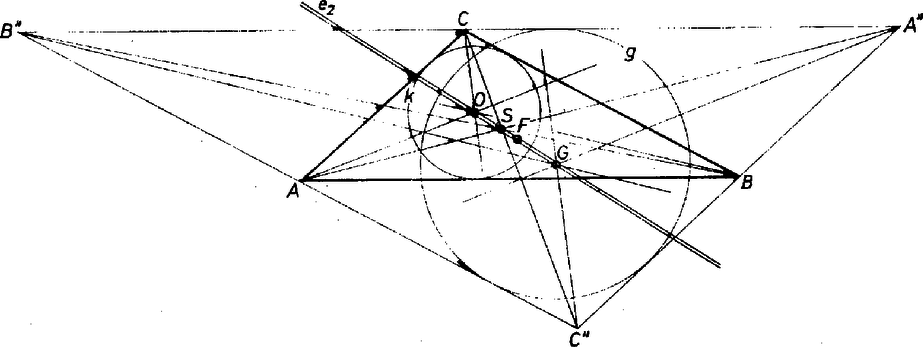5. ábra

Bizonyítás. Az

A B C

háromszög ugyanúgy kapható meg

A'' B'' C''

-ből, mint

A' B' C'

A B C

-ből. Ezért a 3. tétel szerint

G

S

O

egy egyenesre illeszkednek, és

G S = 2 O S

. Tehát

G

és

F

rajta vannak az

O S

egyenesen, és

G F = G S - F S = O S + F S = O F

(esetleg a négy pont azonos).
A cikk elején mondott dualitásban a két Euler egyenes egymásnak felel meg, az

A'' B'' C''

háromszög beírt köre pedig az

A B C

háromszög Feuerbach körének a párja. Jelöljük ezt a kört

g

-vel, mint látni fogjuk, ennek a körnek további nevezetes tulajdonságai vannak.

5. tétel. Ha meghúzzuk az

A B C

háromszög csúcsaiból a

g

-hez tartozó második érintőket⁴ (6. ábra,

g_{a}

g_{b}

g_{c}

), három érintőnégyszöget kapunk (beírható körrel vagy hozzáírt körrel), amelyeket két érintő és két háromszög-oldal határol. (Az érintők azokból a csúcsokból indulnak, ahol az

A B C

háromszög két kiválasztott oldala nem metszi egymást. Az

A B C

háromszöget tehát három különböző módon is érintőnégyszöggé alakíthatjuk úgy, hogy ‐ szemléletesen szólva ‐ egy-egy oldalát "behorpasztjuk''⁵.)
Azt, hogy hogyan lehet eldönteni, hogy egy ilyen négyszögnek a kör beírt vagy hozzáírt köre lesz-e, a legegyszerűbben a 6. ábra

A B E C

négyszögén tudjuk megmutatni. Az érintő körnek először is benne kell lennie a

B A C

szögtartományban, másrészt a

g_{b}

(ill.

g_{c}

) érintőt ugyanazon a félegyenesen kell érintenie, mint

g

. Most tehát a négyszögnek beírt köre van, amit az

A B

A C

oldalak és a

B E

C E

oldalak meghosszabbításai érintenek.⁶

6. ábra

Bizonyítás. (Zárójelben utalunk majd azokra a módosításokra, amik akkor szükségesek, ha

E

a háromszögön kívül van. Hozzáírt kör esetén hasonló a bizonyítás, amit az olvasó a 7. ábra alapján maga végiggondolhat.)
Azt kell belátnunk, hogy

A C + B E = A B + C E

, vagyis

B E - C E = c - b

. Jelöljük a

g_{a}

g_{b}

g_{c}

egyenesek érintési pontjait

G_{a}

-val,

G_{b}

-vel,

G_{c}

-vel, és legyenek

T_{a}

T_{b}

T_{c}

azok a pontok, amelyekben az

A'' B'' C''

háromszög oldalai

g

-t érintik. Jelöléseink mellett (6. ábra)

\begin{matrix} B E - C E = B G_{b} - E G_{b} - C E = B T_{b} - E G_{c} - C E = B T_{b} - C G_{c} = \\ = B T_{b} - C T_{c} = A'' T_{b} - A'' B - (A'' T_{c} - A'' C) = c - b . \end{matrix}

E

a háromszögön kívül van, akkor

\begin{matrix} B E - C E = B G_{b} + E G_{b} - C E = B T_{b} + E G_{c} - C E = B T_{b} + C G_{c} = B T_{b} + C T_{c} = \\ = (A'' T_{b} - A'' B) - (A'' T_{c} - A'' C) = c - b . \end{matrix}

g_{a}

g_{b}

g_{c}

, érintőknek egy további tulajdonságát figyelhetjük meg, ha meghúzzuk

g

-nek az

A'' B'' C''

háromszög oldalaival párhuzamos második érintőit. Ezek az

A B C

háromszöghöz középpontosan hasonló

A_{1} B_{1} C_{1}

háromszöget határoznak meg (7. ábra). A hasonlóság

H

középpontja a második Euler egyenesen van, és

H O = O G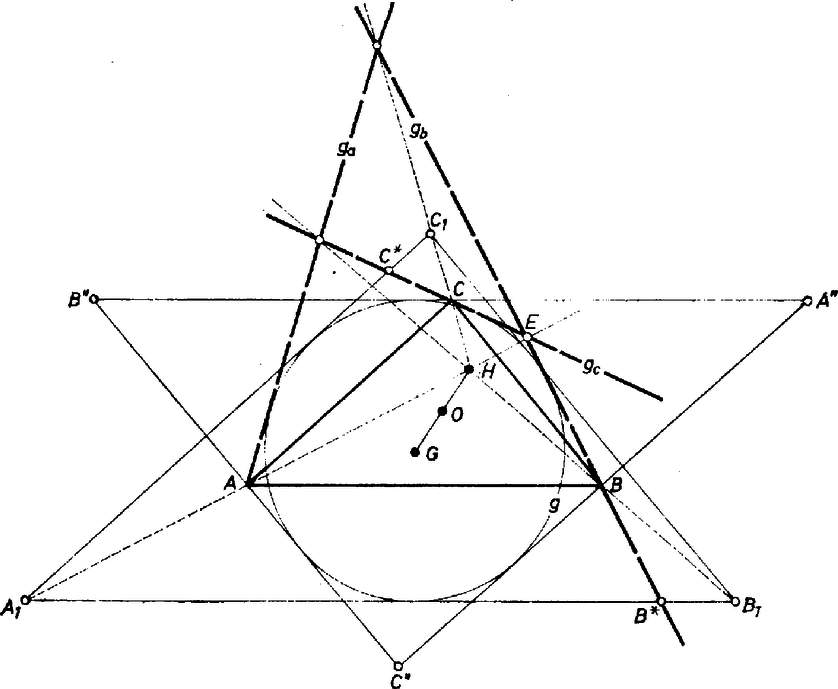

7. ábra

6. tétel. Az

A A_{1}

B B_{1}

C C_{1}

egyeneseket a

g_{a}

g_{b}

g_{c}

érintők közül kettő-kettő ugyanabban a pontban metszi. (Pl.

A A_{1}

-en van

g_{b}

és

g_{c}

már ismert metszéspontja,

E

.⁷)

Bizonyítás. Megmutatjuk, hogy

A A_{1}

egyenes illeszkedik

E

-re. Az

A B E C

és

A_{1} B^{*} E C^{*}

négyszögek érintőnégyszögek, és megfelelő oldalaik párhuzamosak vagy azonosak (

B^{*}

g_{b}

A_{1} B_{1}

-en,

C^{*}

g_{c}

A_{1} C_{1}

-en levő pontja). Az 5. tételben megadott kritériumok szerint (amelyek eldöntik, hogy a szóban forgó négyszögeknek beírt vagy hozzáírt köre van-e) a párhuzamos érintők az érintett köröknek mindig azonos oldalán vannak. Emiatt a két négyszög középpontosan hasonló, és a hasonlóság középpontja

E

. Állításunk ebből már következik.
Mindent összevéve már kilenc érintőt húztunk a

g

körhöz. Így valóban a háromszög Feuerbach körének a párja lehet.
A 3‐6. tételekhez hasonló tételeket mondhatunk ki az oldalfelező külső szögfelezőkre, így további három Euler egyenest kapunk.
Végül felsoroljuk az általunk javasolt dualitás legfontosabb megfeleltetéseit:

\begin{matrix} \begin{matrix} Az oldalfelező szögfelezők párhuzamosak a szögfelezőkkel. \\ Az oldalfelező szögfelezők a középháromszög szögfelezői. \\ F,S,Oegy egyenesre illeszkednek, ésO S = 2 F S(második Euler egyenes). \\ HaO-t tükrözzükF-re, a kapottGpont a kétszeres háromszög beírt körének a középpontja. \end{matrix} & \begin{matrix} A magasságvonalak párhuzamosak az oldalfelező merőlegesekkel. \\ A magasságvonalak a csúcsokon át a szemközti oldallal párhuzamosan húzott egyenesek által határolt kétszeres háromszög oldalfelező merőlegesei. \\ M,S,Kegy egyenesre illeszkednek, ésM S = 2 K S(első Euler egyenes). \\ AK Mszakasz felezőpontja a középháromszög körülírt körének a középpontja (Feuerbach kör). \end{matrix} \end{matrix}

3. Megjegyzések

Célunk annak megmutatása volt, hogy a nevezetes pontok {

S

K

O

M

} halmaza egy ötödik ponttal,

F

-fel bővíthető. Ezt indokolja e pontok tulajdonságainak a vizsgálata, és alátámasztja ezt a pontok síkbeli elhelyezkedése is (4. ábra).
Ha vesszük a háromszög beírt körének a középpontját (

O

), a súlypontot (

S

), a körülírt kör középpontját (

K

) és vesszük a megfelelő pontokat a középháromszögben és a megkétszerezett háromszögben, akkor olyan rendszert kapunk, amely még jobban alátámasztja az általunk javasolt módosítást:
⁸

\begin{matrix} \begin{matrix} a középháromszög \\ a háromszög \\ a megkétszerezett háromszög \end{matrix} & \begin{matrix} FSK' \\ OSK \\ GSM8 \end{matrix} \end{matrix}

\begin{matrix} * * * \end{matrix}

Felhívjuk a téma iránt érdeklődő olvasók figyelmét a következő feladatokra és a velük kapcsolatos nevezetes összefüggésekre:

a) Horvay Katalin ‐ Reiman István: Geometriai feladatgyűjtemény, I. kötet
    1376 ‐ 1379 (Euler egyenes, oldalfelező szögfelezők),
    1380 ‐ 1388 (Feuerbach kör),
    1389 ‐ 1394 (Simson egyenes),
    1526 ‐ 1528 (szögfelezők),
    1266 ‐ 1267 (érintőnégyszögek).1389 ‐ 1394 (Simson egyenes),
    1526 ‐ 1528 (szögfelezők),
    1266 ‐ 1267 (érintőnégyszögek).
b) KöMaL 59. kötet 3‐4. szám OKTV döntő mat. II. tantervűek 1. feladata.
c) D. O. Sklajarszkij-N. N. Csencov-I. M. Jaglom: Válogatott feladatok és tételek az elemi matematika köréből 2/1 kötet: 112‐114, 147 (nevezetes vonalak),
118‐121 (Euler egyenes, Feuerbach kör, Simson egyenes),
135 (Newton és Gauss tétele):
d) Matematikai Versenytételek I. kötet. Az 1897. évi versenyhez csatlakozó 2. jegyzet az "adott körbe és egyszersmind adott kör köré írt háromszögekről'' (40. oldal).

A fordító

¹Megjelent a Praxis der Mathematik 1967. évi 9. számában.

¹Vizsgálataink közben egyeneseknek tekintjük a háromszög transzverzálisait, így például $f_{a}$ , $f_{b}$ , $f_{c}$ egyeneseket jelölnek, és a háromszög oldalain is azok egyenesét értjük. "Felezőpontjuk'' és "hosszuk'' azonban a háromszögben az oldalszakaszoknak lesz, és $a$ -val, $b$ -vel, $c$ -vel az oldalak hosszát jelöljük.

²Általában három azonos jellegű nevezetes vonal közül csak az egyikről beszélünk.

³A $T_{2}$ fölött álló csillag értelme később derül ki.

¹ $^{*}$ Most látszik, hogy szerencsésebb lett volna $T_{2}$ -ben azt megkövetelni, hogy az egyenes legyen párhuzamos a belső szögfelezővel. Enélkül nehéz a kétféle szögfelezőt megkülönböztetni. (A fordító)

⁴Előfordulhat, hogy ezek azonosak az első érintőkkel (vagyis $A'' B'' C''$ oldalaival).

⁵Ha két érintő azonos, akkor a megfelelő négyszög háromszöggé fajul.

⁶Pontosabb volna, ha négyszögek helyett egyenes-négyesekről beszélnénk.

⁷Ha két érintő párhuzamos, akkor az az egyenes is párhuzamos velük, amelyiken a metszéspontjuknak rajta kellene lennie. ("Végtelen távoli'' metszéspont.) Ha az érintők azonosak, akkor alkalmas pontjukat választjuk metszéspontjuknak.

⁸ Tehát $F$ az $O'$ -t, $G$ az $O''$ -t, $M$ a $K''$ -t jelöli.