Cím: Az ikozi-dodekaéder pályázat eredménye
Szerző(k):  Csirmaz László 
Füzet: 1982/március, 107 - 111. oldal  PDF  |  MathML 
Témakör(ök): Egyéb (KöMaL pontverseny is)

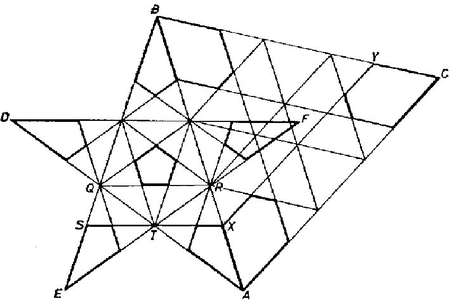
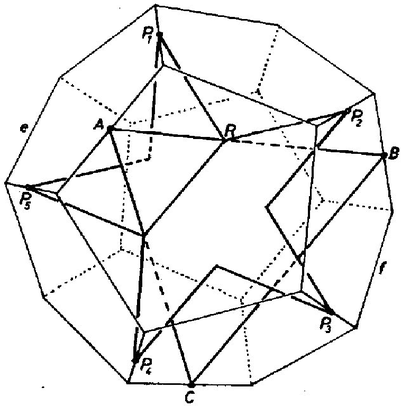
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

 

A fényképen látható csillagtest, a nagy ikozi-dodekaéder modelljének elkészítésére, valamint a fénykép melletti ábra magyarázatára az 1981. évi novemberi számunkban pályázatot írtunk ki. Erre összesen 15 pályamunka (16 modell) érkezett. A fődíjat, egy Go játékkészletet
 

CSILLAG PÉTER (Budapest),

 

a Landler Jenő Híradástechnikai és Gépészeti Szakközépiskola II. osztályos tanulója kapta a szépen elkészített modellért és az ábra érdembeli magyarázatáért.
A gondosan, pontosan elkészített modellért 100‐100 forintos könyvutalványt kaptak (betűrendben) :
   Búza Kinga  (Kaposvár),   Szabó Gyöngyi  (Szentes),   Tigelmann Péter  (Mágocs).
A többi pályamunka beküldői közül Ladányi László (Miskolc), Pintér Gábor (Kiskunhalas) és Tar Tibor (Keszthely) egy-egy könyvet, míg Dobos Balázs és Dobos Sándor (Budapest), Fekete György (Sajókeresztúr), Juhász István (Pátroha), Molnár Ágnes (Kecskemét), Molnár Endre (Budapest), Párkányi Rita (Balassagyarmat), Nagy Katalin (Szécsény), Szász Károly (Sükösd), Szászi Attila (Tamási) munkája elismeréseként egy-egy emléklapot kapott.
 

*

 

A csillagtestnek ‐ ahogyan azt a pályázat kitűzésekor említettük ‐ összesen 32 lapja van. Ebből 12 szabályos csillagötszög, a többi 20 pedig szabályos háromszög. Ezek azonban nem lapok a szokásos értelemben: egymást keresztül-kasul átjárják. (Ezzel kapcsolatban érdemes megnézni. Bakos Tibor: Megjegyzések az F. 2307. feladathoz című cikkét a KÖMAL 1981. évi 7. számában az 53. oldalon.) Pályázóink mindegyike rájött arra, hogy a megmagyarázandó 2. ábrán éppen vastagon kihúzott "részlapok'' azok, melyeket a többi lap nem takar el, s hogy a csillagtestet ezekből lehet összeállítani. A magyarázatok alapján a pályázók lényegében két csoportra oszthatók. Az egyik csoport tagjai azt mutatták meg, hogy az összeállításnál az egymás mellé kerülő részlapok élei egyenlő hosszúak ‐ például hogy az ABC háromszögben az A csúcsnál található ötszög A-val szemközti oldala ugyanolyan hosszú, mint a csillagötszög belső kis ötszögének oldala stb. A másik csoport tagjai azt igyekeztek igazolni, hogy a részlapokból összeálló csillagtestben (ha az valóban összeáll) a csillagötszög és a háromszög részlapjai egy síkban vannak. Egyedül Csillag Péter volt az, akinek lényegében sikerült igazolnia, hogy az ábrán meghúzott szakaszok a különböző csillagötszög és háromszög alakú lapok metszésvonalai, bár nem tudott számot adni a csillagtest általa felhasznált szimmetriatulajdonságairól.
 
1. ábra
 
2. ábra

A pályázat egyik tanulsága: pályázóink egyike sem kételkedett ‐ még egy pillanatra sem ‐ abban, hogy az elkészítendő test létezik! Természetesen a pályázat szövege ezt sugallta, sőt a modell elkészítése után ki-ki kezébe foghatta, forgathatta: tessék, itt van! De vajon az elkészült test valóban test-e a szó matematikai értelmében is ‐ azaz a lapok síklapok, az élek egyenes szakaszok, a csúcsok pedig pontok? Bizonyára nem! A következő (jól ismert) példa mutatja, hogy nem minden esetben hihetünk a "kézzelfogható tényeknek''. Egy 13 cm oldalú négyzetet vágjunk szét négy darabra, úgy, ahogyan azt a 3. ábra mutatja. A részekből egy 8×21-es téglalap állítható össze. (Tessék kipróbálni!) Ugyanakkor 132=169 és 8⋅21=168, tehát az összerakással valami baj van!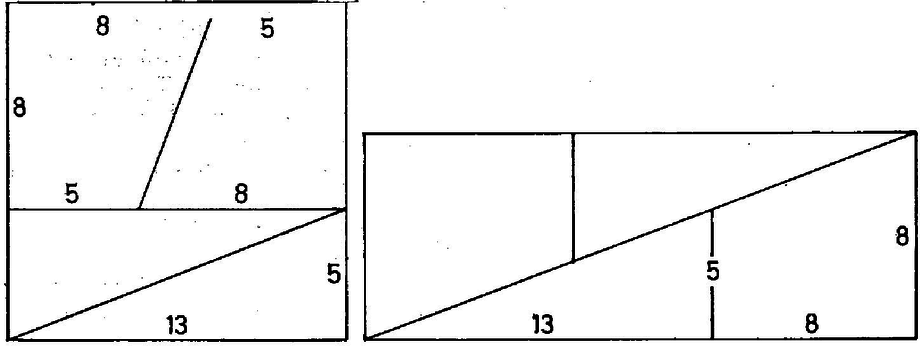
 
3. ábra

A csillagtest létezésével kapcsolatos gondok azonnal eltűnnének, ha találnánk olyan jól ismert poliédert, melyből csonkolással vagy valamilyen más módon megkaphatjuk a csillagtestet (lásd Bérczi Szaniszló: Szabályos és félig szabályos testek periódusos rendszere, KÖMAL, 1979. 10. szám, 193. oldal). Többen észrevették, hogy ha a testet vékony gumihártyával vonjuk be ‐ azaz vesszük a konvex burkot ‐ akkor olyan testet kapunk, melyet csupa szabályos ötszög és szabályos háromszög határol. Ez utóbbit pedig megkaphatjuk úgy, hogy egy szabályos dodekaéder csúcsait levágjuk (4. ábra). Így a csillagtest csúcsai ‐ legalábbis megérzésünk szerint ‐ egy szabályos dodekaéder élfelező pontjai (5. ábra).
 
4. ábra
 
5.ábra

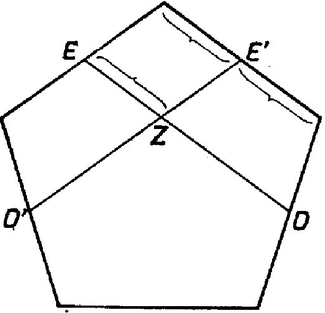
Lássuk, igaz-e ez az állítás ! Ennek érdekében induljunk el az ellenkező irányból. Vegyünk fel egy szabályos dodekaédert, és nézzük azt a 12 szabályos ötszöget, melyek csúcsai az élfelező pontok közül kerülnek ki, s melyek síkjai a dodekaéder egy-egy lapjával párhuzamosak. Az ilyen ötszögek egyikét a 6. ábrán kettős vonallal jelöltük. Minden ilyen ötszögben vegyük az átlók által meghatározott csillagötszöget. Ennek a 12 csillagötszögnek az oldalaiból további szabályos háromszögek is kialakulnak (szabályosak, hiszen mindhárom oldaluk ugyanolyan hosszú), ilyen például az ABC vagy az A'B'C' háromszög. Minden ötszögátlóra pontosan egy csillagötszög és pontosan egy háromszög illeszkedik, az átlók száma 5⋅12=60, tehát a háromszögek száma 60/3=20. Állítjuk, hogy a csillagötszögeket, illetve a szabályos háromszögeket a többi lap éppen azokban a szakaszokban metszi, amelyek a 2. ábrán szerepelnek. Ebből és a dodekaéder szimmetriáiból már következik, hogy ez a csillagtest ikertestvére annak, aminek a fényképe az 1. ábrán látható. Így nemcsak a 2. ábra "magyarázatát'' adtuk meg, hanem egy csapásra elintéztük azt a problémát is, hogy létezik-e az elkészítendő test.
A háromszög, illetve csillagötszög lapokra vonatkozó állításokat éppen a dodekaéder szimmetriaviszonyai miatt elegendő, mondjuk, az ABC háromszögre és az ABEFD csillagötszögre (illetve bármely másikra) igazolni. Sőt elég csak annyit megmutatni, hogy a lapok egy-egy csúcsánál pontosan azok az alakzatok jönnek létre, amelyeket a 2. ábrán vastag vonallal megjelöltünk.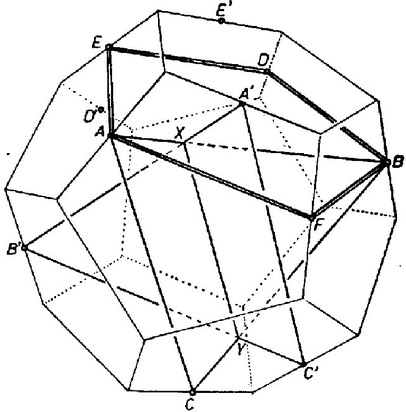
 

6. ábra
Szemeljük ki tehát az ABC háromszöget és annak is az A csúcsát. Ezt a lapot az A csúcshoz "közel'' két háromszöglap és egy csillagötszöglap metszi, a két háromszöglap egyike A'B'C'. Ám A és A',  B és B', valamint C és C' egymás tükörképei a dodekaéder egy Σ szimmetriasíkjára. Ezért például az AB és A'B' szakaszok is egymás tükörképei, tehát metszik is egymást a Σ szimmetriasík egy X pontjában. Továbbá AA' és CC' párhuzamosak, másrészt egyenlők is (mindkettő a dodekaéder egy-egy lapjának két szomszédos élfelező pontját köti össze). Tehát az ACC'A' négyszög téglalap, és az AC, A'C' egyenesek párhuzamosak Σ-val. Ebből már következik, hogy az ABC és A'B'C' lapok XY metszésvonala párhuzamos AC-vel.
 
7. ábra
 
8. ábra

Következő feladatunk az AX távolság meghatározása. Tudjuk, hogy AB párhuzamos ED-vel (AB átló az AFBDE szabályos ötszögben), és ugyanezért A'B' párhuzamos E'D'-vel. Másrészt AE∥A'E' (mert mindkettő párhuzamos a dodekaéder egy élével), tehát az AEZX négyszög paralelogramma, ahol Z az ED és E'D' szakaszok metszéspontja (7. ábra). Így AX=EZ, s ez utóbbi a 7. ábra alapján a dodekaéder élhosszának felével egyenlő.
Térjünk most vissza a 2. ábrához. Ott az AXSE négyszög egy XS oldalú szabályos ötszög része. Ez az ötszög szükségképpen egybevágó a dodekaéder lapjaival, hiszen ez utóbbi méretét az élfelező pontok közti AE távolság egyértelműen meghatározza. Ezért SX hossza egyenlő a dodekaéder élével, a 2. ábrán látható AX távolság, pedig ennek, s így a dodekaéder élének is fele. Az ABC háromszöglapon tehát az AC-vel párhuzamos XY metszésvonal valóban ott van, ahol az a 2. ábrán szerepel. Ezzel persze azt is megmutattuk, hogy XY-t az ABC háromszög szimmetriatengelyeire tükrözve szintén metszésvonalakat kapunk.
Azt kell még megvizsgálnunk, hogy hol tűnik el az ABC lap a "hasát'' felénk mutató P1P3P5P2P4 csillagötszög alatt (8. ábra). Az AP1 valamint BP3 szakaszok párhuzamosak, hiszen AP1 párhuzamos az e éllel, BP3 pedig az f éllel, és e és f egymás tükörképei a dodekaéder középpontjára. Ezért AB és P1P3 is metszi egymást egy R pontban, és AR és RB aránya megegyezik az AP1 és BP3=P1P5 szakaszok arányával, vagyis egy szabályos ötszög oldalának és átlójának arányával.
Visszatérve ismét a 2. ábrára, ARQE egy szabályos ötszög négy egymás utáni csúcsa, továbbá AQ=BR, tehát AR és RB aránya megegyezik egy szabályos ötszög oldalának és átlójának arányával. Így az ABC háromszög és a csillagötszöglap metszésvonala átmegy a 2. ábrabeli R ponton, és természetesen átmegy az AC szakaszt ugyanilyen arányban osztó ponton is ‐ tehát párhuzamos BC-vel. Ezzel igazoltuk, hogy az ABC háromszöglapból pontosan azok a részek "látszanak'', amelyek a 2. ábrán vastag vonallal vannak elkerítve.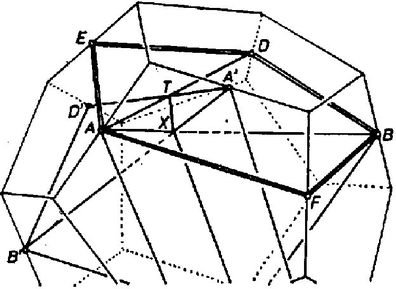
 
3. ábra

Nézzük most az ABEFD csillagötszöget! Éppen az előbb igazoltuk, hogy az egyik háromszöglap éppen az QR szakaszban metszi, tehát a csillagötszöglap közepéből pontosan az a szabályos ötszög látszik ki, amely a 2. ábrán vastagon van kihúzva. Az maradt csak hátra, hogy az ötszög A csúcsánál létrejövő deltoid oldalait határozzuk meg. Ezek egyikét a B'A'D' csúcsú csillagötszög metszi ki (9. ábra). Láttuk, hogy az AB és A'B' szakaszok egymást az X pontban metszik, tehát a metszésvonal egyik pontja X. Mivel D és D' is tükörképei egymásnak a dodekaédernek arra a Σ szimmetriasíkjára, melyre A és A' (valamint B és B') is egymásnak tükörképei, ezért az AD és A'D' szakaszok is metszik egymást, mondjuk egy T pontban. A kérdéses metszésvonal pedig éppen a Σ sík TX egyenese. Mivel AE párhuzamos Σ-val, továbbá AE és TX egy síkban vannak (az AFBDE ötszög síkjában), azért TX párhuzamos AE-vel. Ez pedig azt jelenti, hogy a 2. ábrán a T pont az AD egyenesnek és az X-ből húzott AE-vel párhuzamos egyenesnek a metszéspontja, vagyis SX felezőpontja. Ezzel megmutattuk, hogy a csillagötszögből is a többi lap a vastag vonallal megjelölt részeket metszi ki. Ezzel a 2. ábra magyarázatának is a végére értünk.
Végül figyelmébe ajánljuk mindazoknak a borítón látható félig szabályos csillagtestet, akik kedvet kaptak ezek modelljeinek elkészítésére, de a nagy ikozi-dodekaéder túl nagy falatot jelentett számukra.