Cím: 1981. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldása
Szerző(k):  Surányi János 
Füzet: 1982/február, 50 - 61. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Legyenek A, B, P, Q, R egy sík pontjai. Bizonyítsuk be, hogy

AB¯+PQ¯+QR¯+RP¯≤AP¯+AQ¯+AR¯+BP¯+BQ¯+BR¯.
(XY¯ jelöli az X, Y pontok távolságát.)
 

Megoldás. Mielőtt a tulajdonképpeni megoldásra térnénk, megjegyezzük, hogy a feladat szövege nem zárja ki, hogy a pontok közül több, akár mind az 5 egy egyenesre essék, sőt a bizonyítandó egyenlőtlenség még akkor is érvényes, ha több pont egybeesik. Ha egy K és L pont egybeesik, akkor a KL (zárt) szakaszon a K(=L) pontot értjük, a hossza pedig 0. A háromszög-egyenlőtlenség továbbra is érvényes a következő alakban: a tetszés szerinti K, L, M pontokra
KL¯+KM¯≥LM¯,
és itt abban az esetben érvényes az egyenlőség jele, ha K az LM szakasz pontja.
 

1. ábra
 

A feladatra térve, annak állítását az említett legáltalánosabb értelmezés mellett bizonyítjuk. Két esetet különböztetünk meg. Az első, ha a P, Q, R pontok között van kettő, mondjuk P és Q, amelyekre az AQ és BP szakaszoknak van egy M közös pontja (1. ábra.) Ez más szóval azt jelenti, hogy ABQP konvex négyszög, amely egyenes szakasszá is fajulhat, ha a négy pont egy egyenesen van, vagy háromszöggé, ha három pont egy egyenesen van; esetleg két szomszédos csúcs egybeesik. Ilyenkor MAB-re és MPQ-ra alkalmazva a háromszög-egyenlőtlenséget
MA¯+MB¯≥AB¯,MP¯+MQ¯≥PQ¯.
Itt
MA¯+MQ¯=AQ¯,MB¯+MP¯=BP¯,
így a két egyenlőtlenség megfelelő oldalait összeadva azt nyerjük, hogy
AQ¯+BP¯≧AB¯+PQ¯.

Bárhol fekszik is az R pont, APR-re és BQR-re alkalmazva a háromszögegyenlőtlenséget
AP¯+AR¯≥PR¯,BQ¯+BR¯≥QR¯.
Az utolsó három egyenlőtlenség megfelelő oldalait összeadva a bizonyítandó összefüggést kapjuk.
Az olyan eseteket kell még megvizsgálnunk, amelyekben bármely kettőt jelenti is U és V a P, Q, R pontok közül, AU-nak és BV-nek nincs közös pontja. Ez esetben mind az 5 pont különböző, és sem PQ, sem QR, sem PR nem párhuzamos AB-vel. Ha ugyanis A és B, vagy A és P, vagy B és Q, vagy P és Q egybeesnék, vagy ha PQ és AB egy irányban párhuzamos volna, akkor AQ-nak és BP-nek volna közös pontja, az első négy esetben éppen az egybeeső pontpár.
A P, Q, R pontok közül legalább kettő az AB egyenesnek ugyanarra a partjára vagy az egyenesre esik. Jelöljük ezek közül a távolabbit, illetőleg a legtávolabbit P-vel, a másikat Q-val, ha pedig R is erre az oldalra esik, az legyen az AB egyeneshez legközelebbi. Ekkor a PQ egyenes belső pontban metszi az AB szakaszt, mert különben ABPQ vagy ABQP konvex négyszög volna, s így átlóinak volna közös pontja.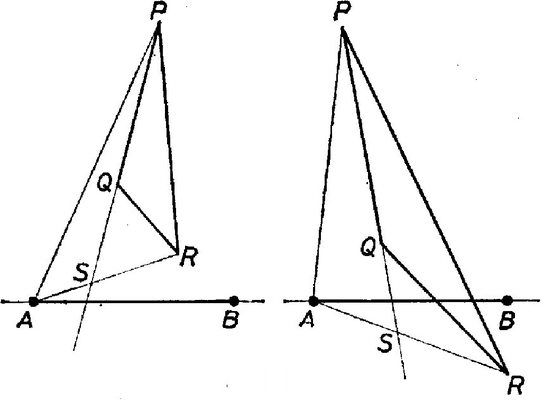

2. ábra

Ha P, Q, R nincs egy egyenesen, feltehetjük, hogy a PQ egyenes elválasztja A-t és R-et (2. ábra). Ekkor az APR háromszög tartalmazza (belsejében vagy a határán) Q-t. AR és PQ metszéspontját jelöljük S-sel. Alkalmazzuk a háromszög-egyenlőtlenséget az APS háromszögre (ez nem elfajuló, mert A nincs a PS egyenesen), és SQR-re:
AP¯+AS¯>PS¯,SQ¯+SR¯≥QR¯.
Itt
AS¯+SR¯=AR¯,PS¯=PQ¯+SQ¯.
A két egyenlőtlenség megfelelő oldalait összeadva, figyelembe véve a két egyenlőséget és mindkét oldalról elhagyva a QS¯ távolságot, azt kapjuk, hogy
AP¯+AR¯>PQ¯+QR¯.
(Mivel az egyik esetben nem állhat fenn egyenlőség, így az összeadással keletkezett egyenlőtlenségben sem.)
Alkalmazzuk a háromszög-egyenlőtlenséget QAB-re és BPR-re:
QA¯+QB¯≥AB¯,BP¯+BR¯≥PR¯.
Az utolsó három egyenlőtlenség megfelelő oldalait összeadva ebben az esetben is a bizonyítandó egyenlőtlenséget kapjuk. Ezzel a feladat állítását bebizonyítottuk.
 

Megjegyzések. 1. A bizonyítás során a háromszög-egyenlőtlenség következő két következményét bizonyítottuk be és használtuk fel:
a) Konvex négyszög átlói hosszának az összege nagyobb, mint két szemközti oldal hosszának az összege.
b) Ha az ABC háromszög tartalmazza a D pontot, de D különbözik A-tól, akkor
AB¯+AC¯>DB¯+DC¯.
Mindkét állítás igaz elfajuló sokszögekre is, ha ,,nagyobb'' helyett ,,nagyobb vagy egyenlőt'' mondunk. Az első állításban, ha két szomszédos csúcs egybeesik, akkor az ebből a pontból a másik két pontba vezető szakaszok szemben fekvő oldalaknak számítanak, de egyben ezek a négyszög átlói is. Így ha ezt a két szemben fekvő oldalt vesszük, akkor egyenlőség áll fenn. (Ha a másik két szemben fekvő oldalt tekintjük, azok közül az egyik 0 hosszúságú, s így a háromszög-egyenlőtlenséget kapjuk.) A bizonyítást elemezve láthatjuk, hogy még egy esetben áll fenn egyenlőség: ha a négy pont egy egyenesen van, a szemközti oldalpárnak tekintett két szakasz egyirányú és van közös pontjuk.
Mindkét alakzat a második állítás elfajuló esetének is tekinthető: az előbbi annak a fönt kizárt esetnek, ha D egybeesik A-val, a második pedig annak, amikor a háromszög csúcsai egy egyenesen vannak, továbbá A és D a BC szakasz pontjai. A bizonyítást elemezve látható, hogy csak ezekben az esetekben állhat fenn egyenlőség.
2. Nézzük meg, a feladat állításában mikor állhat fenn egyenlőség. Láttuk, hogy a bizonyítás második részében ez nem következhet be, mert az első rész-egyenlőtlenségben nem állhat fenn egyenlőség.
A bizonyítás első részében a négyszögre vonatkozó egyenlőtlenségben akkor áll fenn egyenlőség, ha A és P egybeesik (ettől nem lényegesen különböző eset, ha B és Q esik egybe) vagy ha AB és PQ egy egyenesnek két egyirányú szakasza, amelyeknek van közös pontjuk (a 0 hosszúságú szakaszt minden szakasszal párhuzamosnak és egyirányúnak tekintjük). A további két egyenlőtlenségben akkor lesz az egyenlőség jele érvényes, ha A a PR szakasznak, B pedig a QR szakasznak pontja.
Ha A és P egybeesik, akkor az utolsó előtti követelmény R helyzetétől függetlenül teljesül, így akkor lesz a feladat állításában az egyenlőség jele érvényes, ha R a QB szakasz B-n túli meghosszabbításán van. Egyik lehetőségnek azt kaptuk tehát, hogy A és B egyike a PQR háromszög egyik csúcsával esik egybe, a másik pedig a szemközti oldalszakasz pontja.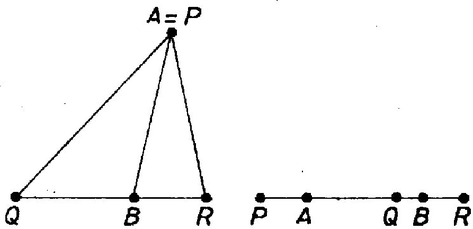

3. ábra

Ha A,B,P és Q egy egyenesen van, akkor az utolsó két követelmény akkor és csak akkor teljesül, ha R is ezen az egyenesen van, továbbá A és B a másik három pont közti két, közös belső pont nélküli szakasz egyikének, ill. másikának pontja (3. ábra).
3. Általánosan igaz, hogy ha A1,A2,...,An és B1,B2,...,Bn+1 egy sík pontjai, akkor az A-k közti szakaszok és a B-k közti szakaszok hosszának összege nem nagyobb, mint az összes AiBj távolságok összege. n=1-re a háromszög-egyenlőtlenséget kapjuk; az n=2 eset bizonyítása volt a kitűzött feladat. Nagyobb n értékek esetére egy hasonló jellegű bizonyítási kísérlet áttekinthetetlenné válnék. A gömb már több lehetőséget kínál a rá vonatkozó megfelelő állítás bizonyítására. Ez után a sugár minden határon túli növelésével látható be, hogy az állításnak a síkban is igaznak kell lennie. Ennek a részleteibe azonban nem bocsátkozunk bele.
 

2. Legyen n 2-nél nagyobb páros szám. Egy n×n-es sakktábla mezőit kiszínezzük n22 színnel úgy, hogy minden színű mezőből pontosan kettő van. Bizonyítsuk be, hogy el lehet helyezni n bástyát csupa különböző színű mezőre úgy, hogy semelyik kettő se üsse egymást.
 

I. megoldás. Két bástya akkor ütheti egymást, ha egy sorban vagy egy oszlopban vannak. Mivel n bástyát kell elhelyeznünk, ezért olyan elhelyezéseket keresünk, amelyeknél minden sorban és minden oszlopban egy bástya áll, továbbá mindegyik bástya mezeje más-más színű. Válasszuk külön a kétféle követelményt: számláljuk először össze, hányféleképpen helyezhetünk el n bástyát úgy, hogy ne üthessék egymást, azután vizsgáljuk meg, hány olyan lehet az elhelyezések közül, amelyik nem tesz eleget a mezők színére tett követelménynek.
Kezdjük a bástyák elhelyezését az első sorral, ide n-féleképpen tehetjük le az első bástyát. Mind az n kezdést (n-1)-féleképpen folytathatjuk, mivel a második sorba ‐ a már letett bástya oszlopát kivéve ‐ bármelyik mezőre tehetjük a következő bástyát. Az első két sorba tehát n⋅(n-1)-féleképpen helyezhetünk bástyát úgy, hogy ne üthessék egymást. Ezután a harmadik sorban mindig (n-2) hely áll rendelkezésre a harmadik bástya számára, és így tovább. Az első (n-2) bástya megfelelő elhelyezése után az (n-1)-edik sorban még két hely áll rendelkezésre az utolsó előtti bástya elhelyezésére, és ha ezt is letettük az egyikre, ezzel az utolsó bástya helye is már meg van határozva. Az n bástyát tehát1
n⋅(n-1)⋅(n-2)⋅...⋅2=n!
elrendezésben helyezhetjük az n×n-es sakktáblára úgy, hogy semelyik kettő ne üthesse egymást.
Ha mármost egy ilyen elhelyezésben két bástya azonos színű mezőn áll, akkor az elhelyezés megsérti a színezésre vonatkozó kívánalmat, bárhogy helyezkedjék is el a többi bástya. A további (n-2) bástyát (n-2)!-féleképpen helyezhetjük el. Mivel n2/2 szín mindegyikével két-két mezőt színeztünk ki, és ezeknek a mezőpároknak bármelyikén állhat a kívánalmat megsértő két bástya, ezzel már elrontva a bástyaelhelyezést, így legfeljebb
(n-2)!⋅n22
bástyaelhelyezés nem felel meg a színezési feltételnek az n! közül. A mindkét követelményt kielégítő bástyaelhelyezések száma tehát nem kevesebb, mint
n!-(n-2)!⋅n22=(n-2)!⋅[n(n-1)-n22]=(n-2)!n2⋅(n-2).
Ez pozitív egész szám minden 2-nél nagyobb páros n-re, és ezekre mindig van a feltételeket kielégítő bástyaelhelyezés, amint azt a feladat állította.
Hozzátesszük, hogy n=2-re a feladat állítása nem igaz, amint azt a 2×2-es táblának a 4. ábra szerinti színezése mutatja. (Lásd 56. oldal).
 

Megjegyzések. 1. A továbbiakban kényelmes lesz felhasználni a következő észrevételt. A feladat szempontjából lényegtelen a sorok és az oszlopok sorrendje, mert ha van egy bástyaelhelyezés és két sort vagy két oszlopot felcserélünk a bennük elhelyezett bástyákat velük mozgatva, akkor a keletkezett új bástya-elhelyezésben két bábu akkor és csak akkor ütheti egymást, ha az eredeti elhelyezésben is üthették egymást; továbbá nem változik az sem, hogy milyen színű mezőn álltak az egyes bástyák.
2. A problémát kiterjeszthetjük páratlan n-ekre úgy, hogy (n2-1)/2 szín mindegyikével 2-2 mezőt színezünk ki és a fennmaradó mezőnek vagy egy további színt adunk, vagy megtiltjuk, hogy arra bástya kerüljön.
Az első esetben a fenti módon számolva azt kapjuk, hogy a mindkét követelményt kielégítő bástyaelhelyezések száma nem kevesebb, mint
n!-(n-2)!⋅n2-12=(n-1)!⋅n-12.
Ez minden 1-nél nagyobb páratlan számra pozitív egész, n=1-re pedig magától értetődő módon igaz a feladat állítása. Az első értelmezés mellett tehát minden páratlan n számra elhelyezhető n bástya az n×n-es sakktáblán úgy, hogy különböző színű mezőkön álljanak, és semelyik kettő ne üthesse egymást.
Ha pedig egy mező tiltott a bástyák számára, akkor kezdjük ennek a sorában a bástyák elhelyezését. Ezt (n-1)-féleképpen tehetjük meg. A következő sorba ismét (n-1)-féleképpen helyezhetünk bástyát, mert itt csupán az első bástyával nem kerülhet egy oszlopba az újabb bástya. Tovább mindig eggyel csökken az újabb bástya számára szóba jövő mezők száma, így ha az n×n-es sakktáblán van egy tilos mező, akkor (n-1)!⋅(n-1)-féleképpen helyezhetünk el úgy bástyákat, hogy ne legyenek köztük ütő helyzetben levők. A színezési feltételt nem kielégítő elhelyezések száma most sem nagyobb, mint
(n-2)!⋅n2-12.
így a mindkét követelménynek megfelelő elhelyezések száma legalább
(n-1)!⋅(n-1)-(n-2)!⋅n2-12=(n-1)!⋅n-32.
Ha tehát n>3, akkor a második értelmezés mellett is van megfelelő bástyaelhelyezés. Az eddigiek azonban még nem zárják ki, hogy a 3×3-as sakktáblán is legyen, hiszen csak alsó becslést nyertünk a megfelelő elhelyezések számára.
3. Vizsgáljunk meg egy 3×3-as sakktáblát egy tilos mezővel. (Az 1. megjegyzés szerint feltehetjük, hogy ez a bal alsó sarok). Ezt úgy akarjuk kiszínezni, hogy ne lehessen rajta 3 bástyát a kívánt módon elhelyezni. Jelöljük a sorokat számokkal, az oszlopokat betűkkel, ahogyan a sakkban szokás, a színeket pedig kisbetűkkel. Legyen a C1 mező színe k. Ide csak akkor nem tehetünk bástyát, ha az A2, B3 és A3, B2 mezőpárok vagy egyező színűek, vagy az egyik pár egyező színű, a másikban pedig szerepel a k szín. Mindenképpen feltehetjük, hogy A2 és B3 egyező, mondjuk l színű, mert ha nem így volna, akkor a 2-es és 3-as sor felcserélésével ezt elérhetjük. Az A2, B1, C3 mezőkre akkor nem tehetjük a 3 bástyát, ha az utóbbi kettő egyező m színű. Az A3, B1, C2 ezután csak akkor nem megfelelő bástyaelhelyezés, ha az első és harmadik mező egyező n színű, végül a még lehetséges A3, B2, C1 elhelyezés sem megfelelő, mivel B2 eleve már csak k színű lehet.
 
4. ábra
 
5. ábra

Azt találtuk tehát, hogy ha páratlan n-re egy n×n-es sakktábla egy mezejét elhagyjuk, a többit kiszínezzük úgy, hogy minden színnel két mező legyen kiszínezve, akkor n>3-ra továbbra is elhelyezhető n bástya a kívánt módon, n=3-ra azonban nem feltétlenül. A fenti gondolatmenet azt is adta, hogy csak az 5a ábra színezése mellett nem lehetséges az elhelyezés, valamint az ebből a felső két sor megcserélésével keletkezőnél (5b ábra). Az utóbbi azonban nem lényegesen különböző, a jobbra emelkedő átlóra történő tükrözéssel és a színek alkalmas átkeresztelésével keletkezik az 5a ábra színezéséből.
Figyeljük meg a továbbiak érdekében azt is, hogy ennek a ,,rossz'' elhelyezésnek minden 2×2-es résztáblájában legalább az egyik átló mezői különböző színűek.
4. Tardos Gábor észrevette, hogy n növekedésével a tiltott mezők számát is növelhetjük. Pontosabban, ha n>3 és az n×n-es sakktáblából n/2-nél kevesebb mezőt elhagyunk, a többit pedig kiszínezzük úgy, hogy egy színnel legfeljebb két mező legyen színezve, akkor is elhelyezhető n bástya úgy, hogy semelyik kettő ne üthesse egymást és csupa különböző színű mezőn álljanak. Páros n esetén tehát (n-2)/2 mezőt hagyhatunk el, páratlan n esetén (n-1)/2-t.
Ennek belátására gondoljuk meg, hogy egy kizárt mező (n-1)! bástyaelhelyezést hiúsít meg, tehát ha t tilos mező van, ez legfeljebb t⋅(n-1)! elhelyezést zár ki. A megmaradó mezőkből1 [12(n2-t)] egyszínű pár alkotható és ezek legfeljebb ugyanennyiszer (n-2)! bástyaelhelyezést zárhatnak ki. A megfelelő bástyaelhelyezések száma tehát legalább
(n-2)!{(n-1)(n-t)-[12(n2-t)]}==(n-2)!{n2-nt-n+t-12(n2-n)-[12(n-t)]}==(n-2)!{12n(n-2t-1)+t-[12(n-t)]}.
A középső kifejezést úgy kaptuk, hogy alkalmaztuk a következő könnyen belátható összefüggést: ha u egész szám, akkor
[u+v]=u+[v],
éspedig u=12(n2-n)-re. (Ez a kifejezés nyilvánvalóan egész szám).
Ha az utolsó alakba t helyébe (n-2)/2-t teszünk páros n esetén, illetőleg (n-1)/2-t páratlan n esetén, akkor (n-2)! szorzójára a következők adódnak:
n-1-[n+24],ill.n-12-[n+14].
Ha n 3-nál nagyobb egész szám, akkor a megfelelő kifejezés pozitív. Ezzel az állítást bebizonyítottuk.
A nyert eredmény azt adja többek közt, hogy 4×4-es sakktáblára egy tiltott mező esetén is elhelyezhető 4 bástya a kívánt módon, 5×5-ös táblára pedig 2 tiltott mező esetén is 5 bástya. Megmutatható, hogy ennél több is igaz: 4×4-es sakktábla esetén tetszés szerinti 2 mezőre megtilthatjuk bástya helyezését, 5×5-ös tábla esetén pedig már 5 mezőre, amik nincsenek egy sorban vagy egy oszlopban, akkor is lehetséges a bástyák kívánt módon történő elhelyezése.
Az I. megoldás meggyőzött arról, hogy létezik a követelményeknek megfelelő bástyaelhelyezés, sok is, anélkül, hogy eljárást adott volna ilyen elhelyezés megkeresésére. A következő megoldásban egy ilyen eljárás megadásával bizonyítjuk az állítás igaz voltát.
 

II. megoldás. A következő, a feladaténál valamivel általánosabb állítást fogjuk bebizonyítani: Ha n egy 3-nál nagyobb egész szám, és egy n×n-es sakktáblán egy mezőt tiltottnak nyilvánítunk, a többit kiszínezzük úgy, hogy legfeljebb 2 mező lehet egyező színnel festve, akkor elhelyezhető a táblán a bástya úgy, hogy semelyik 2 ne üthesse egymást és csupa különböző színű mezőn álljanak.
Helyezzük az első bástyát a tiltott mező sorának bármelyik megengedett mezejére. Ekkor a többi bástya a többi sorokban helyezendő el úgy, hogy a már letett bástyáétól különböző oszlopban álljon, és amennyiben van még egy, a lehelyezett bástyáéval egyező színű mező a tábla még megengedett részén, arra sem kerülhet bástya. Az (n-1) bástya számára megengedett mezők tehát egy (n-1)×(n-1)-es résztáblát adnak, esetleg egy tiltott mezővel. Ha ilyen nem adódik, akkor önkényesen nyilvánítsunk tiltottnak egy mezőt, ezzel visszavezettük a feladatot az eredetire, csak n helyett (n-1)-gyel. Az eljárást ismételjük addig, amíg vissza nem jutunk egy 4×4-es táblához egy tiltott mezővel, legyen ez A1.
Ketté választjuk a lehetőségeket. Először azt az esetet vizsgáljuk, amikor az A oszlopban vagy az 1-es sorban van olyan mező, amelyikkel egyező színű található a jobb felső 3×3-as résztáblán. Legyen pl. B1 és D2 színe k. (L. 6. ábra). Ekkor A2 színe egy újabb l szín. A jobb felső 2×2-es résztáblának az egyik átlójában esetleg fellép a másik l színű mező, de az egyik átlónak egyszínűnek kell lennie. Mondjuk C4 és D3 m színű. A4 és C2 egyező n színű kell hogy legyen, mert csak így nem ad megfelelő bástyaelhelyezést B1, C3-mal, amelyekkel egyező színű mezőket már ismerjük. Hasonlóan, egyező p színűnek kell lennie B3-nak és C1-nek, mert különben A4, D2-vel ad egy megfelelő bástyaelhelyezést. A2, B3, C4 ezután D1-gyel már csak akkor nem megfelelő 4 bástya elhelyezésére, ha az utolsó mező l színű. Ekkor azonban B4 egy újabb színnel van színezve, és így A2, B4, C1, D3 alkalmas a 4 bástya elhelyezésére (6. ábra).

6. ábra

Azt az esetet kell még megvizsgálnunk, ha minden A oszlopbeli mezővel egyszínű ‐ ha van ilyen egyáltalán ‐ az 1-es sorban van és viszont. Ilyen párnak nyilvánvalóan kell lennie. Legyen A2 és B1 k színű. B3 és C4 egyező l színű, mert A2, D1-gyel csak így nem adnak megfelelő bástyaelhelyezést, miután egyikük sem lehet D1-gyel egyező színű. Hasonlóan C2, D3 egyező m színű kell hogy legyen. A4, B3, C2, D1 csak akkor nem megfelelő, ha az első és utolsó mező, egyező n színű, A4, B1, C3, D2 pedig csak akkor, ha az utolsó kettő egyező p színű. Ekkor azonban A2, B4, C3, D1 megfelelő bástyaelhelyezést ad, mert B4 színe különbözik az eddig említett mezők színétől. Ezzel beláttuk, hogy n=4-re megoldható feladtunk és ezzel a megoldást befejeztük (7. ábra).
 


7. ábra

Megjegyzés. A fenti gondolatmenet alkalmazásával lényegesen tovább lehet menni a kizárható mezők kérdésében, mint amennyi az I. megoldás gondolatmenetével elérhető volt. Bebizonyítjuk, hogy ha n legalább 5, akkor a II. megoldás állítása még akkor is érvényes marad, ha előre kijelölt n-3 mezőre nem szabad bástyát helyezni.
A II. megoldás második részében bebizonyítottuk az állítás igaz voltát n=4-re. Ha n>4, akkor egy bástya elhelyezésével legalább 2 tiltott mezőt zárhatunk ki a továbbiakból. Ha van legalább 2 tiltott mező egy sorban vagy egy oszlopban, akkor ezek sorába, ill. oszlopába helyezünk egy bástyát, ha pedig ilyen nem fordul elő, akkor egy tiltott mező sorának és egy másik oszlopának a közös mezejére. Az elhelyezett bástya mezejével egyszínű mező viszont a továbbiak szempontjából tiltott mezővé válik. Így egy bástya elhelyezésével a problémát egy 1-gyel rövidebb oldalú tábla esetére vezettük vissza, amelyen legalább 1-gyel kevesebb a tiltott mezők száma.
Az eljárást n-4-szer ismételve egy 4×4-es résztáblához jutunk, amelyen legfeljebb 1 tiltott mező van, tehát elhelyezhető rajta 4 bástya a kívánt módon. Ezzel beláttuk állításunkat.
A kizárható mezők száma ezen túl is növelhető. Erre más alkalommal szándékszom visszatérni.
 

3. Az n természetes számot osszuk el rendre az 1,2,3,...,n számokkal és jelöljük a maradékok összegét r(n)-nel. Bizonyítsuk be, hogy végtelen sok olyan k természetes szám van, amelyre r(k)=r(k-1).
 

Megoldás. Azon, hogy egy n egész számot egy pozitív egész számmal maradékosan osztunk, egy
n=cq+r
alakú előállítását értjük, ahol q (a hányados) egész szám, r pedig (a maradék) kisebb, mint c és nem negatív. Ilyen hányados és maradék mindig van és mindig csak egy.
Vizsgáljuk n és n-1 maradékát ugyanazzal a k számmal történő osztásnál. Ha a fenti osztásnál az r maradék nem 0, akkor
n-1=cq+(r-1),
és mivel a maradék egyértelműen meg van határozva, így minden ilyen esetben 1 adódik hozzá az r(n)-r(n-1) különbséghez. Ha viszont r=0, vagyis c osztója n-nek, akkor
n-1=c(q-1)+c-1,
tehát az n osztói az osztónál 1-gyel kevesebbel csökkentik a fenti különbséget. Jegyezzük meg, hogy magával n-nel n-et még el kell osztanunk a feladat szövege szerint, n-1-et azonban már nem. Ezt az osztót azonban figyelmen kívül is hagyhatjuk, mert az elvégzendő osztás maradéka 0. Jelöljük az n szám n-nél kisebb (pozitív) osztóinak összegét s(n)-nel, számukat d(n)-nel, akkor megállapításaink szerint
r(n)-r(n-1)=n-d(n)-1-(s(n)-d(n))=n-1-s(n).

A feladat eszerint annak a belátását kívánja, hogy végtelen sok olyan k szám van, amelyikre
s(k)=k-1.
Az első néhány szám kipróbálása azt mutatja, hogy a 2 hatványai ilyenek, és valóban könnyű belátni, hogy k=2l minden pozitív egész l kitevőre kielégíti az egyenletet. Valóban, 2l nála kisebb osztói 1,2,22,...,2l-1. Ezek mértani sorozatot alkotnak, amelyben az elemek összege ‐ mivel az elemek száma l, a hányados pedig 2 ‐
[2l-1]2-1=2l-1=k-1.
Ezzel állításunkat igazoltuk.
 

Megjegyzések. 1. A feladat igen hasonló a tökéletes számok problémájához. A fenti jelöléseket használva akkor neveztek az ókori görögök tökéletesnek egy számot, ha
s(k)=k.
Már Euklidész elemeiben szerepel, hogy a 2s-1(2s-1) alakú számok tökéletesek, ha a második tényező törzsszám. Mintegy 2000 évvel később Euler bebizonyította, hogy a páros számok közül csak az Euklidész által említett számok tökéletesek.
Páratlan tökéletes szám nem ismeretes. Számos olyan tulajdonságot találtak, amivel minden páratlan tökéletes számnak ‐ ha van ilyen ‐ rendelkeznie kell. A legkisebb szám is, amelyiknek mindez a tulajdonsága megvan, elképzelhetetlenül nagy kell hogy legyen, azt azonban nem sikerült eddig bebizonyítani, hogy nincs páratlan tökéletes szám.
A 2s-1 alakú szám könnyen láthatóan csak akkor lehet prím, ha s is prímszám, de távolról sem igaz, hogy minden s prímszámra prímszámot adna a fenti formula. Pl.
211-1=2047=23⋅89.
Eddig a nagyteljesítményű számítógépek segítségével is mindössze 27 ilyen alakú prímet találtak, így ugyanennyi az ismert tökéletes számok száma is. Nem tudjuk, hogy van-e több, még azt sem sikerült azonban eldönteni, hogy van-e végtelen sok, vagy pedig véges a páros tökéletes számok száma.
2. Az
s(k)=k-1
egyenletről azt láttuk be, hogy 2 minden hatványa megoldása, tehát végtelen sok megoldása van. Nem tudjuk azonban, hogy van-e más megoldása is, mint a 2 hatványai. Annyit nem nehéz belátni, hogy egy 2lm alakú szám, ahol m páratlan (l lehet 0 is) csak akkor elégítheti ki az egyenletet, ha m egy egész szám négyzete.
3. A bizonyítás során nyert
r(n)-r(n-1)=n-1-s(n)
formulát n=2,3,...,k-ra összeadva és felhasználva, hogy r(1)=0, azt kapjuk, hogy
r(k)=(r(k)-r(k-1))+(r(k-1)-r(k-2))+...+(r(2)-r(1))+r(1)==(k-1)+(k-2)+...+1-s(k)-s(k-1)-...-s(2)=k(k-1)2-S(k),
ahol S(k)-val a következő összeget jelöltük:
S(k)=s(k)+s(k-1)+...+s(2).
[Az összeghez s(1)-et is hozzáírhatjuk, ha tetszik, mert annak értéke 0.]
Célszerűbb s(k) helyett az összes osztók σ(k) összegét használni. A kettő kapcsolata
σ(k)=s(k)+k.
A σ(k)+σ(k-1)+...+σ(1) összeget ∑(k)-val jelölve
S(k)=σ(k)-k+σ(k-1)-(k-1)+...+σ(1)-1=∑(k)-k(k+1)2.
Ezt r(k) képletébe beírva az egyszerűbb
r(k)=k2-∑(k)
formulát kapjuk.
Néhány versenyző felhasználta, hogy n-et c-vel maradékosan osztva a hányados [nc], azaz n=c⋅[nc]+r, ahol 0≤r<c,
továbbá az irodalomra hivatkozva1 a
∑(n)=[n1]+2[n2]+...+n[nn]
formulát. Ezekből eljutott az r(n)-re éppen nyert képlethez és azt vette segítségül a feladat megoldásához (nem mindig sikerrel).
 Surányi János
1Ezt a számot ,,n faktoriálisnak'' nevezik, és ‐ mint azt használtuk is ‐ így jelölik: n! Lényegében azt láttuk be, hogy n különböző dolgot ennyiféleképpen lehet egymás után rakni.

1[t]-vel, mint szokásos, a legnagyobb egész számot jelöljük, amelyik még nem nagyobb t-nél, a t úgynevezett egész részét.

1 D. O. Skljarszkij‐N. N. Csencov‐J. M. Jaglom: Válogatott feladatok és tételek az elemi matematika köréből 1. Aritmetika és algebra 172. o.