Kezdőlap


Cím:	Az 1981. évi (12.) Nemzetközi Fizikai Diákolimpia feladatai
Füzet:	1981/november, 161 - 165. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Légüres térben vízszintesen fekszik egy $m_{1}$ tömegű henger, amelyben a térfogat felében egy $m_{2}$ tömegű dugattyú van rögzítve ( $1.$ ábra). Az elzárt részben $n mol M$ molekulatömegű és $T_{0}$ hőmérsékletű gáz van. A dugattyú rögzítése hirtelen megszűnik, majd a dugattyú elszabadulása után a gáz szabadon kiáramlik. Mekkora lesz a henger végsebessége?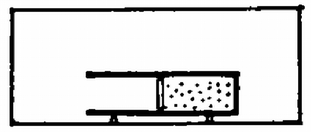
Elhanyagolandó minden súrlódás, a henger és dugattyú hőfelvétele, valamint a folyamat első részében a gáz súlypontjának elmozdulása. Számadatok: $T_{0} = 273 K$ , $m_{1} = 0, 6 kg$ , $m_{2} = 0, 3 kg$ , $n = 25 mol$ , hélium esetében a molekulatömeg $4$ , $C_{v} = 12, 8 joule/mol K$ , $κ = 5 / 3$ .

1. ábra

Megoldás. A folyamat első része adiabatikus kiterjedés; kétszeres térfogatra kiterjedve (

2.

ábra) a hőmérséklet

T

les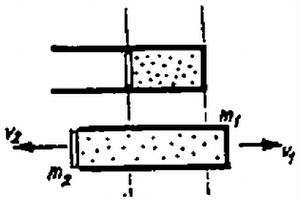z.

2. ábra

Az adiabatikus állapotváltozás törvénye szerint:

\begin{matrix} T_{0} V_{0}^{κ - 1} = T {(2 V_{0})}^{κ - 1}, \end{matrix}

innen

T = T_{0} / 2^{κ - 1}

.
A henger és dugattyú mozgási energiáját a gáz belső energiájának csökkenése fedezi:

\begin{matrix} n C_{v} (T_{0} - T) = \frac{m_{1} v_{1}^{2}}{2} + \frac{m_{2} v_{2}^{2}}{2} . \end{matrix}

Az impulzustétel szerint:

\begin{matrix} m_{2} v_{2} = m_{1} v_{1} . \end{matrix}

Az egyenletrendszer megoldása adja a henger sebességét a folyamat első részének végén:

\begin{matrix} v_{1} = \sqrt[]{\frac{2 n C_{v} (T_{0} - T)}{m_{1} [1 + (m_{1} / m_{2})]}} . \end{matrix}

A folyamat első részének végső pillanatában tehát a henger jobbra mozog

v_{1}

sebességgel, a dugattyú pedig már éppen kiesett. Ettől kezdve rögzítsük koordináta-rendszerünket a hengerhez. Adva van a vákuumban egy nyitott henger, amelyben

n M

tömegű,

T

hőmérsékletű gáz van. Ez a gáz nyilván balra kiáramlik és a hengert jobbra löki

v_{κ}

sebességgel. A gáz molekuláinak mozgási energiája:

\begin{matrix} \frac{n M \cdot v_{m}^{2}}{2} = \frac{3}{2} \cdot n R T, \end{matrix}

tehát a gázmolekulák átlagos repülési sebessége:

\begin{matrix} v_{m} = \sqrt[]{\frac{3 R T}{M}} . \end{matrix}

Egyensúlyban a molekulák egyhatod része repül az egyes koordináta-tengelyek irányában ide és oda. A kiáramlást úgy fogjuk számolni, hogy feltételezzük: a kiáramlás során végig igaz lesz, hogy a molekulák

1 / 6

része repül a cső fenekének. Tudjuk azonban, hogy ez csak első közelítésben van így. Tehát

n M / 6

tömeg

v_{m}

sebességgel repül a henger fenekének, ott rugalmasan ütközik. Ezután a henger

v_{κ}

, a gáz

v_{g}

sebességgel mozog. Rugalmas ütközés esetében az impulzus megmaradásán kívül a mozgási energia is megmarad. Az impulzus megmaradása szerint:

\begin{matrix} \frac{n M}{6} \cdot v_{m} = \frac{n M}{6} \cdot v_{g} + m_{1} v_{κ} . \end{matrix}

Az energiamegmaradás törvénye szerint:

\begin{matrix} \frac{n M v_{m}^{2}}{6 \cdot 2} = \frac{n M v_{g}^{2}}{6 \cdot 2} + \frac{m_{1} v_{κ}^{2}}{2} . \end{matrix}

Az egyenletrendszer megoldása adja a henger sebességét a gáz kiáramlása után:

\begin{matrix} v_{κ} = \frac{2 n M}{6 m_{1} + n M} \cdot v_{m} = \frac{2 n M}{6 m_{1} + n M} \cdot \sqrt[]{\frac{3 R T}{M}} . \end{matrix}

A gázmolekulák egyhatoda

v_{g}

sebességgel pattan vissza, amelynek abszolút értéke kisebb, mint

v_{m}

. A gáz szükségképp valamelyest lehűl, mert belső energiájának csökkenéséből fedezi a henger (újabb) mozgási energiáját.
Összesítve a henger sebessége:

v_{1} + v_{κ}

.
Számadataink szerint

n M = 0, 1 kg

T = 171, 17 K

v_{1} = 283 m/s

v_{2} = 566 m/s

v_{m} = 1026 m/s

v_{g} = - 972 m/s

v_{κ} = 55, 5 m/s

. A henger teljes végső sebessége:

\begin{matrix} 283 m/s + 55, 5 m/s = 338, 5 m/s . \end{matrix}

2. Egy

U_{0} = 4, 5 volt

mellett működő,

R_{0} = 2 ohm

ellenállású fogyasztót

U = 6 volt

elektromotoros erejű, elhanyagolható belső ellenállású akkumulátorról kell működtetnünk, és ezért egy csúszó érintkezős ellenállásból feszültségosztót (potenciométert) állítottunk össze.
a) Az a kívánság, hogy a hatásfok (a fogyasztó és az egész berendezés teljesítményének hányadosa) ne legyen kisebb, mint

η = 0, 6

. Mekkora legyen a változtatható ellenállás és legalább mekkora áramerősséget kell kibírnia?
b) Milyen körülmények között lesz a hatásfok a lehető legnagyobb és mekkora ez a hatásfok?

Megoldás. a) A fogyasztón minden esetben

I_{0} = U_{0} / R_{0} = 2, 25

amperes áram folyik keresztül és teljesítménye

P_{0} = U_{0} I_{0} = U_{0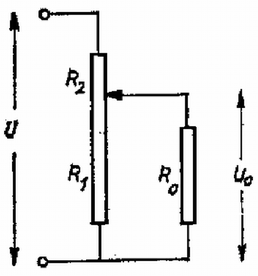}^{2} / R_{0} = 10, 125

watt (

3.

ábra).

3. ábra

Legyen a feszültségosztó részeinek ellenállása

R_{1}

és

R_{2}

. A berendezésen átfolyó teljes áramerősség

I_{t}

, és az összes felhasznált teljesítmény:

\begin{matrix} P_{t} = U I_{t} . \end{matrix}

A hatásfok:

\begin{matrix} η = \frac{P_{0}}{P_{t}} = \frac{U_{0}^{2}}{U R_{0} I_{t}} . \end{matrix}

(1)

Minthogy

U_{0}

U

R_{0}

adott mennyiségek, látható, hogy a hatásfok fordítva arányos a teljes áramerősséggel. Az áramerősség, ha a hatásfok

0, 6

\begin{matrix} I_{t} = \frac{U_{0}^{2}}{U R_{0} η} = 2, 81 A . \end{matrix}

Ezt kell kibírnia a huzalellenállás

R_{2}

ellenállású részének.
A huzalellenállás felső részének ellenállása Ohm törvénye szerint:

\begin{matrix} R_{2} = \frac{U - U_{0}}{I_{t}} = 0, 53 Ω . \end{matrix}

Az alsó rész ellenállása pedig:

\begin{matrix} R_{1} = \frac{U_{0}}{I_{t} - I_{0}} = 8 Ω . \end{matrix}

A huzalellenállás összesen

8, 53

ohmos.

b) az (1) egyenlet alapján látható, hogy esetünkben a hatásfok csak a teljes áramerősségtől függ. A hatásfok akkor lesz a lehető legnagyobb, ha

I_{t}

a lehető legkisebb. Ez minimális, ha

I_{1} = 0

, vagyis

R_{1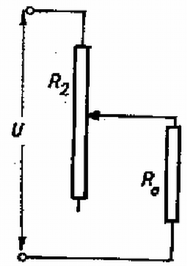} = \infty

(4. ábra).

4. ábra

A kapcsolásból előtétellenállás lesz. Ekkor

\begin{matrix} R_{2} = \frac{U - U_{0}}{I_{0}} = 0, 67 ohm és a hatásfok: \\ η = \frac{U_{0}^{2}}{U R_{0} I_{0}} = \frac{U_{0}^{2}}{U U_{0}} = \frac{U_{0}}{U} = 0, 75. \end{matrix}

3. Egy rádiócsillagászati obszervatórium tengerparton levő rádióvevőjét

h = 2

méter magasan helyezték el a tenger szintje felett. A vevő csak az elektromos térerő vízszintes összetevőjét érzékeli. Egy

λ = 21

centiméteres hullámhosszú elektromágneses hullámot kibocsátó rádiócsillag felkel a horizont fölé és ekkor a vevő maximumokat és minimumokat észlel.

a) Az érkező rádióhullámok milyen iránya esetében észlelnek maximumokat és minimumokat? A független változó az érkező hullámok irányának szöge a vízszinteshez képest.
b) Növekszik vagy csökken az intenzitás közvetlenül azután, hogy a csillag megjelent a horizont felett?
c) Hogyan alakul a felfogott jelek egymásutáni maximumainak és minimumainak intenzitásaránya?

Megjegyzés. A visszavert és érkező hullámok amplitúdóinak aránya

(n - sin ϑ) / (n + sin ϑ)

, ahol

ϑ

a hullám érkezési irányának szöge a vízszinteshez képest és

n

a törésmutató, amely a víz és rövid elektromágneses hullámok esetében

9

-cel egyenlő.

Megoldás. a) A vevőbe a rádióhullámok részben közvetlenül, tehát visszaverődés nélkül, részben pedig a tengerről való visszaverődés után juthatnak be. (A többszörösen visszavert sugarak hatását elhanyagoljuk.) A közvetlenül érkező és a visszavert sugarak különböző utat tesznek meg, ezért fázisuk a detektorban különböző lesz; interferálnak.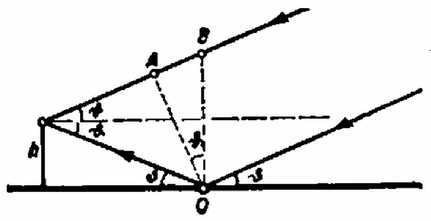

5. ábra

A geometriai útkülönbséget könnyen meghatározhatjuk az

5.

ábra alapján:

\begin{matrix} A B = 2 h sin ϑ . \end{matrix}

Az interferencia maximum- és minimumhelyek kiszámításához még azt is figyelembe kell vennünk, hogy visszaverődéskor

λ / 2

fázisugrás következik be; a maximum feltétele tehát:

\begin{matrix} 2 h sin ϑ_{max} + \frac{λ}{2} = k λ, \end{matrix}

vagyis

\begin{matrix} sin ϑ_{max} = \frac{λ}{2 h} (k - \frac{1}{2}), ahol k = 1,2,3, ... \end{matrix}

(2)

A minimum feltétele:

\begin{matrix} 2 h sin ϑ_{min} + \frac{λ}{2} = (2 k + 1) \frac{λ}{2}, \end{matrix}

vagyis

\begin{matrix} sin ϑ_{min} = \frac{λ}{2 h} k, ahol k = 0,1,2,3, ... \end{matrix}

(3)

b) A felkelés pillanatában

ϑ = 0

, ami (3) szerint minimumot jelent. Tehát

ϑ

növelésével maximum felé haladunk, az intenzitás növekszik.
c) Minimum esetében az eredeti és a visszavert hullámok amplitúdói kivonódnak (

E

az elektromos térerő amplitúdója):

\begin{matrix} E - E \cdot \frac{n - sin ϑ_{min}}{n + sin ϑ_{min}} = \frac{2 sin ϑ_{min}}{n + sin ϑ_{min}} \cdot E . \end{matrix}

Felhasználva (3)-at, ez a különbség

\begin{matrix} \frac{(λ / h) \cdot k}{n + [λ / (2 h)] \cdot k} \cdot E . \end{matrix}

A vétel erőssége az amplitúdó négyzetével arányos, ezért az egymás után következő minimumok intenzitása,

k

értékétől függően (konstans szorzótól eltekintve):

\begin{matrix} {(\frac{(λ / h) \cdot k}{n + [λ / (2 h)] \cdot k})}^{2} \cdot E^{2} . \end{matrix}

Maximum esetében az eredeti és visszavert hullámok amplitúdói összeadódnak:

\begin{matrix} E + E \cdot \frac{n - sin ϑ_{max}}{n + sin ϑ_{max}} = \frac{2 n}{n + sin ϑ_{max}} \cdot E . \end{matrix}

Felhasználva (2)-t, az összeg

\begin{matrix} \frac{2 n}{n + \frac{λ}{2 h} \cdot (k - \frac{1}{2})} \cdot E . \end{matrix}

Az intenzitás az amplitúdó négyzetével arányos, ezért az egymás után következő minimumok intenzitása,

k

értékétől függően:

\begin{matrix} {[\frac{2 n}{n + \frac{λ}{2 h} \cdot (k - \frac{1}{2})}]}^{2} \cdot E^{2} . \end{matrix}

Táblázatunk áttekintést ad a számértékekről:

\begin{matrix} k_{min} & k_{max} & ϑ_{min} & ϑ_{max} & Int. min. & Int. max. \\ 0 & 0 & 0 \\ 1 & 1, 504^{\circ} & 3, 9768 E^{2} \\ 1 & 3, 009^{\circ} & 0, 000136 E^{2} \\ 2 & 4, 517^{\circ} & 3, 9309 E^{2} \\ 2 & 6, 027^{\circ} & 0, 000532 E^{2} \\ 3 & 7, 542^{\circ} & 3, 8858 E^{2} \\ 3 & 9, 062^{\circ} & 0, 00118 E^{2} \end{matrix}

Kísérleti feladat. Egy nem lineárisan nyúló gumiszál elasztikus viselkedését kellett tanulmányozni.