Kezdőlap


Cím:	1981. évi fizika OKTV feladatai
Füzet:	1981/október, 81 - 86. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az I. forduló feladatai

1. Egy

2

méter hosszú pálca közepén csapágyazva van (1. ábra). Az egyik végétől

0,5

méterre egy

3 kg

tömegű test van a pálcára csúsztatva. A pálca tömege a

3 kg

-hoz képest, valamint a súrlódás elhanyagolható;

g = 10 {m/s}^{2}

. A pálcát vízszintes helyzetéből elengedjük. Mekkora sebességgel megy át a pálca vége a függőleges helyzetén?
(Dr. Bodó Zalán)

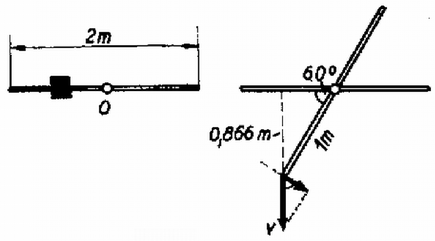1. ábra

Megoldás. A

3 kg

tömegű test szabadon esik. A

0,866

méteres szabadesés végsebessége

v = \sqrt[]{2 g s} = 4,16 m/s

. Ennek érintőleges összetevője a bot végének sebessége:

\begin{matrix} 4,16 \cdot cos 60^{\circ} = 2,08 m/s. \end{matrix}

2. Egy sínen haladó jármű magas rúdra kötött fékező ernyőt vontat

16 m/s

sebességgel (2. ábra). Az ernyő súlya elhanyagolható. Szélcsendes időben a vontatási teljesítmény

32 kW

. Mekkora teljesítmény szükséges a fékező ernyő ugyanazon sebességű vontatásához, ha az útra merőlegesen

12 m/s

sebességű oldalszél fúj?
(Nagy László)

Megoldás. A teljesítmény egyenlő az erő és sebesség szorzatával:

P = F v

. Oldalszél esetében az ernyő levegőhöz viszonyított sebessége:

\sqrt[]{16^{2} + 12^{2}} m/s = 20 m/s

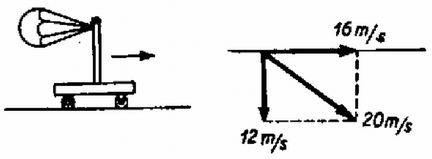2. ábra

Tehát a sebesség

20 / 16

arányában lett nagyobb. Mivel a közegellenállási erő a sebesség négyzetével arányos, ezért a közegellenállási erő

{(20 / 16)}^{2}

arányában növekedett. Azonban ennek az erőnek csak az útmenti összetevője, tehát az eredeti közegellenállási erő

\begin{matrix} {(20 / 16)}^{2} \cdot (16 / 20) = 20 / 16 -szorosa \end{matrix}

végez munkát. A sebesség változatlan, tehát oldalszél esetében a vontatáshoz szükséges teljesítmény:

\begin{matrix} 32 \cdot (20 / 16) kW=40 kW. \end{matrix}

3. Egy mereven összeerősített kettős korong sugarai

r_{1} = 0,3

m és

r_{2} = 0,2

m, tehetetlenségi nyomatéka

Θ = 0,25 kg\cdotm^{2}

. A korong egy légpárnás asztalon fekszik, a súrlódás a korong és az asztal között elhanyagolható (3. ábra). Mindegyik korong peremére egy-egy fonál van felcsévélve. A nagyobbik korong fonalán

m_{1} = 5

kg tömegű test lóg. Mekkora legyen a kisebbik korong fonalán lógó test

m_{2}

tömege, hogy a kettős korong tengelye egyhelyben maradjon?

(g = 10 {m/s}^{2} .)

(Holics László)

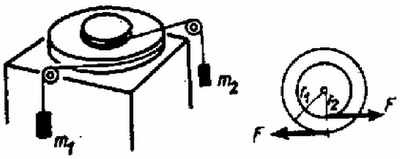3. ábra

Megoldás. A korongra ható erők eredője nulla kell, hogy legyen. Ezért az

F

fonálerőknek egyenlőknek és párhuzamosaknak kell lenniük, ekkor erőpár jön létre, amelynek csak forgatónyomatéka van, de a korong tengelyét nem mozdítja el. A kettős korong

β

szöggyorsulással forog,

m_{1}

gyorsulása (lefelé)

r_{1} β

a fonálerő

F = m_{1} g - m_{1} r_{1} β, m_{2}

gyorsulása (lefelé)

r_{2} β

, a fonálerő

F = m_{2} + m_{2} r_{2} β

. Az erőpár forgatónyomatéka hozza létre a szöggyorsulást:

\begin{matrix} F (r_{1} - r_{2}) = β Θ . \end{matrix}

A kapott egyenletrendszer megoldása:

\begin{matrix} β = \frac{m_{1} g (r_{1} - r_{2})}{Θ + m_{1} r_{1} (r_{1} - r_{2})} = 12,5 s^{- 1}, \\ F = m_{1} g \cdot \frac{Θ}{Θ + m_{1} r_{1} (r_{1} - r_{2})} = 31,25 newton, \\ m_{2} = m_{1} \cdot \frac{Θ}{Θ + m_{1} (r_{1}^{2} - r_{2}^{2})} = 2,5 kg. \end{matrix}

4. Egy kis keresztmetszetű,

U

alakú cső bal oldali, zárt szárában és az alsó vízszintes szárban

5

cm hosszú a higanyoszlop (4. ábra). Ezután a csövet az

O - O

függőleges tengely körül állandó szögsebességgel forgatjuk. Ekkor azt látjuk, hogy a higany pontosan az alsó csövet tölti ki. Mennyi a szögsebesség? A higany sűrűsége

13,6

g/cm

^{3}

, a légköri levegő nyomása

10

newton/cm

^{2}

(ez megfelel

73,5

cm magas higanyoszlop nyomásának).
(Vermes Miklós)

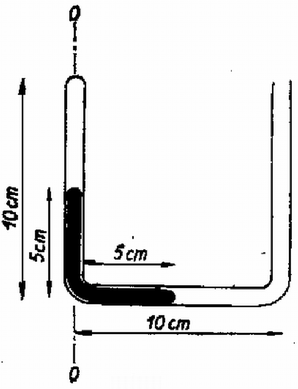4. ábra

Megoldás. A bezárt levegő nyomása a forgatás előtt

\begin{matrix} p_{0} = 10 {N/cm}^{2} - \frac{5 cm}{73,5 cm} \cdot 10 {N/cm}^{2} = 10 {N/cm}^{2} - 0,68 {N/cm}^{2} = 9,32 {N/cm}^{2} . \end{matrix}

Boyle ‐ Mariotte törvénye szerint forgatáskor a bezárt levegő nyomása ennek a fele:

\begin{matrix} p = 4,66 {newton/cm}^{2} = 46 600 P a . \end{matrix}

A

keresztmetszetű esőben a higany tömege

A \cdot l \cdot ϱ

, ahol

l = 10 cm

. Ennek

ω

szögsebességű körpályán tartásához szükséges erő:

\begin{matrix} F = A l ϱ ω^{2} \cdot l / 2 \end{matrix}

(1)

(

l / 2 = 0,05

méter az átlagos rádiusz). Ezt a higanyoszlop végei közötti nyomáskülönbség biztosítja:

\begin{matrix} F = A \cdot (100 000 Pa-46 000 Pa) . \end{matrix}

Egyenlővé téve (1)-et és (2)-t

\begin{matrix} A \cdot 0,1 m \cdot ϱ ω^{2} \cdot 0,05 m = A (100 000 Pa-46 600  Pa) . \end{matrix}

Innen:

ω = 28,02 s^{- 1}

A II. forduló feladatai

1. Egy falban

h = 6 cm

mély,

d = 2 cm

átmérőjű furatot készítünk és ebbe a furatba vékony, merev, elhanyagolható tömegű pálcát dugunk (5. ábra). A súrlódási együttható

μ = 0,2

. Legalább milyen hosszú legyen a pálca, hogy a végére akasztott ruha számára fogasként szolgálhasson?
(Nagy László)

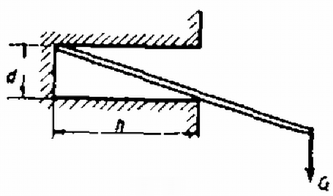5. ábra

Megoldás. A furat alakjára az

α

szög jellemző,

tg α = d / h

(6. ábra).

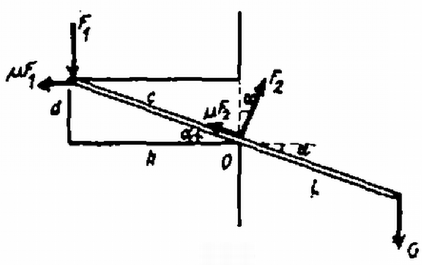6. ábra

Legyen a rúd furatban levő részének hossza

c

, a falon kívül levő részének hossza

L

, a kabát súlya

G

. A megcsúszás kritikus helyzetében mindkét alátámasztási helyen igénybe van véve a maximálisan lehetséges súrlódási erő. Amíg ez a helyzet nem következik be, a feladat statikailag határozatlan.
A fal részéről a rúdra kifejtett erők:

F_{1}, μ F_{1}, 1 F_{2}, μ F_{2}

. Az egyensúly feltétele, hogy a ható erők eredője és a forgatónyomaték nulla legyen. Az erőegyensúly a függőleges és vízszintes komponensekre:

\begin{matrix} G + F_{1} - F_{2} cos α - μ F_{2} sin α = 0, \\ F_{2} sin α - μ F_{2} cos α - μ F_{1} = 0, \end{matrix}

míg a forgatónyomatékok egyenlősége az

O

pontra vonatkozóan:

\begin{matrix} G L cos α = F_{1} c \end{matrix}

Az egyenletrendszer megoldása:

\begin{matrix} F_{1} = \frac{sin α - μ cos α}{2 μ cos α - (1 - μ^{2}) sin α} \cdot G = \frac{5}{3} G = 1,667 G, \\ F_{2} = \frac{μ}{2 μ cos α - (1 - μ^{2}) sin α} \cdot G = \frac{5}{6} \cdot \sqrt[]{10} \cdot G = 2,635 G, \\ L = \frac{(1 + μ tg α) (tg α - μ)}{2 μ - (1 - μ^{2}) tg α} \cdot c = \frac{16}{9} c = 1,778 c . \end{matrix}

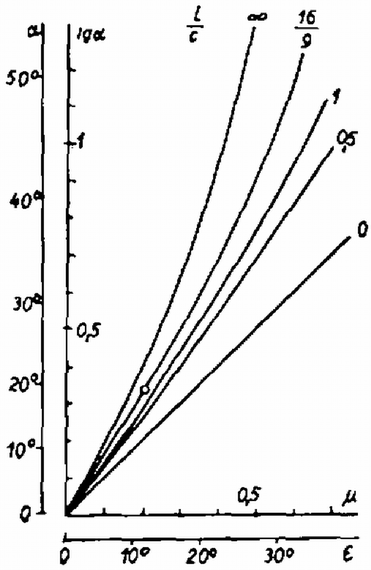7. ábra

A képletünk által adott

L

az a legközelebbi hely, ameddig a terhet közel lehet hozni a megcsúszás veszélye nélkül. Az

L / c

arány a lyuk alakjára jellemző

α

szög és a

μ

súrlódási együttható függvénye. Érdekes megnézni, hogy különböző

L / c

arányok esetében

tg α

, illetőleg

α

hogyan függ a

μ

súrlódási együtthatótól, illetve az

ε

súrlódási határszögtől

(μ = tg ε)

. Feladatunkban

tg α = 1 / 3

és

μ = 0,2 = tg 11,31^{\circ}

, az ezt jelentő helyet megtaláljuk a 7. ábra

L / c = 16 / 9

-hez tartozó görbéjén egy ponttal jelölve. Ábránkról leolvasható, hogy

ε = α

esetében a terhet akárhová akaszthatjuk, mert ekkor

L / c = 0

. A másik határeset, amikor

L / c

végtelen, ez akkor következik be, ha

\begin{matrix} 2 μ - (1 - μ^{2}) tg α = 0 \end{matrix}

Ekkor nem készíthető ilyen módon fogas. Ennek az egyenletnek a megoldása

tg α = 2 μ / (1 - μ^{2})

. Ha arra gondolunk, hogy

μ

a súrlódási határszög tangense, akkor azt kapjuk, hogy

\begin{matrix} tg α = \frac{2 tg ε}{1 - {tg}^{2} ε} = tg 2 ε . \end{matrix}

Tehát a furat alakjára jellemző a szög nem lehet nagyobb a súrlódási határszög kétszeresénél.

2. Egy

1 {dm}^{2}

alapterületű,

2,24

méter magasságú hengerben

4

gramm hélium van

0^{\circ} C

hőmérsékleten és

10 {newton/cm}^{2}

nyomáson (8. ábra). A hengerbe beejtünk egy

80 kg

tömegű dugattyút. Mennyi lesz a dugattyú legnagyobb sebessége? A súrlódást elhanyagolhatjuk. A folyamat olyan gyors, hogy a cső és a dugattyú hőfelvétele elhanyagolható.

g = 10 {m/s}^{2}

. A hélium fajhői

c_{v} = 3,15 = joule/gK

c_{p} = 5,25 joule/gK

.
(Dr. Bodó Zalán)

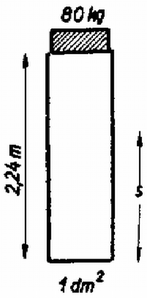8. ábra

Megoldás. A legnagyobb sebességet akkor éri el a dugattyú, amikor gyorsulása nulla, vagyis a rá ható erők eredője zérus. A

80 kg

tömegű dugattyú súlyából

8 {newton/cm}^{2}

nyomás származik, ez a külső légnyomással együtt

18 {newton/cm}^{2}

nyomást jelent. Tehát a gáz nyomásának a gyorsulásmentes pillanatban szintén

18 {newton/cm}^{2}

-nek kell lennie.
A gáz összenyomódása adiabatikus folyamat, a fajhők hányadosa

x = 5 / 3

. Az adiabata törvénye szerint:

\begin{matrix} 10 \cdot 22, 4^{5 / 3} = 18 \cdot V^{5 / 3}, \end{matrix}

innen a keresett térfogat:

V = 22,4 \cdot {(\frac{10}{18})}^{3 / 5} = 15,74 {dm}^{3}

.

Ekkor a

T

hőmérsékletre a gáztörvény alapján:

\begin{matrix} \frac{10 \cdot 22,4}{273 K} = \frac{18 \cdot 15,74}{T}, így T = 1,8 \cdot 0,7 \cdot 273 K=344 K=71^{\circ}C. \end{matrix}

A dugattyúra ható külső erők (a külső légnyomás és a nehézségi erő) nagysága a dugattyú mozgása során állandó, tehát munkavégzésüket egyszerűen megkaphatjuk:

\begin{matrix} W = 1800 N\cdot(2,24 - 1,75) m=1199 joule. \end{matrix}

Ez a munka részben melegíti a héliumot, részben pedig mozgási energiává alakul. A gáz belső energiájának a növekedése a hőmérsékletváltozásból számítható ki:

\begin{matrix} c_{v} m Δ T = 3,15 \cdot 4.71 joule=895 joule. \end{matrix}

A dugattyú mozgási energiája tehát

\begin{matrix} (1199 - 895) joule = 80 (v^{2} / 2), \end{matrix}

innen

\begin{matrix} v = 2,76 m/s . \end{matrix}

A dugattyú sebességének a helytől való függését számítással is követni lehet; így is meghatározhatjuk a sebesség maximumát. A legmélyebb helyzet számítására szolgáló egyenlet magasabb fokú. A helynek, sebességnek, gyorsulásnak, nyomásnak, hőmérsékletnek az időtől való függését csak számítógépes eljárással lehet követni. Ennek a számolásnak az eredményét mutatja a 9. ábra.

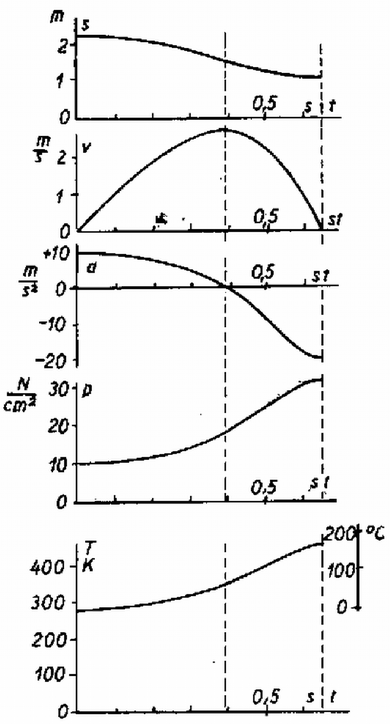9. ábra

Látható, hogy a sebességmaximum kb.

0,395

másodperckor következik be. A dugattyú legmélyebb,

1,089

méteres helyzetét

0,654

másodperckor éri el, amikor is gyorsulása

- 19,08 {m/s}^{2}

, a nyomás ekkor

33,22 {newton/cm}^{2}

, a hőmérséklet

168,2^{\circ} C

. A fékeződés gyorsabban zajlik le, mint a felgyorsulás.

3. A feladat annak megállapítása, mi van az

X

jelzésű dobozban. Ezért a kivezetéseire különböző

ω

körfrekvenciájú váltófeszültséget kapcsolunk és mérjük a bemenő áramerősséget. A dobozra kapcsolt váltófeszültség mindvégig 100 V. A mérések eredményét a 10. ábra és a táblázat mutatja.
(Nagy László)

\begin{matrix} ω(s^{- 1}) & 100 & 200 & 500 & 1000 & 2000 & 5000 & 7500 & 10 000 & 20 000 \\ I(A) & 0,1004 & 0,1015 & 0,1085 & 0,1265 & 0,1581 & 0,1894 & 0,1950 & 0,1971 & 0,1993 \end{matrix}

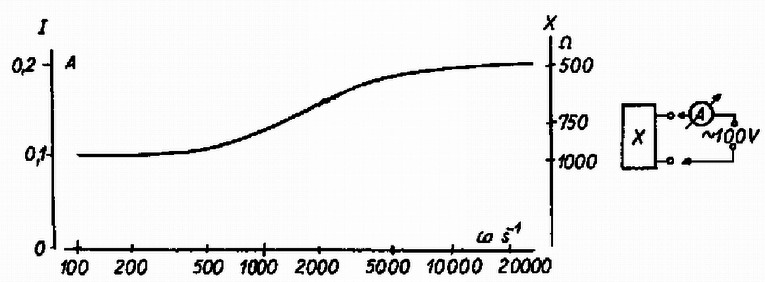10. ábra

Megoldás. Az áramerősség adatait tanulmányozva látjuk, hogy az monoton menetű, nincs rezonanciára utaló szélsőérték, tehát nem lehet a dobozban egyszerre kondenzátor és önindukciós tekercs. Az áramerősségnek a frekvenciával együtt történő monoton növekedése, illetve az impedanciának a monoton csökkenése mutatja, hogy kondenzátor van a dobozban. Látható, hogy

ω = 0

esetében az impedancia

1000

ohm,

ω \to \infty

esetén a határértéke

500

ohm. Tehát a kondenzátoron átfolyó áramnak át kell folynia egy ellenálláson is, különben az impedancia határértéke

ω \to 0

esetén

\infty

ω \to \infty

esetén

0

volna.
Két lehetőséget mutatunk meg, melyek között a mérési adatok alapján nem lehet dönteni (11. ábra).

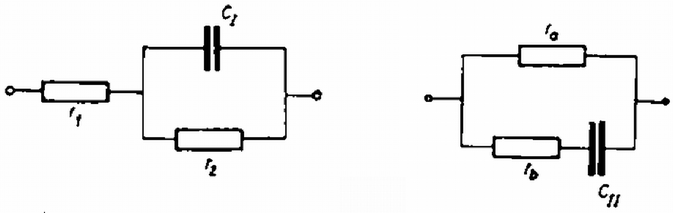11. ábra

I. Ekkor az

ω = 0

esetből

r_{1} + r_{2} = 1000 ohm

adódik és

ω \to \infty

alapján

r_{1} = 500 ohm

.
Az egyenletrendszer megoldása:

r_{1} = r_{2} = 500 ohm

II. Ekkor az

ω = 0

esetből

r_{a} = 1000 ohm

, és

ω \to \infty

alapján

\begin{matrix} r_{a} r_{b} : (r_{a} + r_{b}) = 500 ohm. \end{matrix}

A kapacitás meghatározása céljából le kell vezetni az impedancia

ω

-tól való függését.
I. esetben az eredő ellenállás

\begin{matrix} X = \frac{{(r_{1} + r_{2})}^{2} + {(ω r_{1} r_{2} C_{I})}^{2}}{1 + {(ω C_{1} r_{2})}^{2}}; \end{matrix}

ha ide a táblázat alapján számolt

(ω, X)

értékpárt behelyettesítjük, akkor kapjuk a kondenzátor kapacitására:

\begin{matrix} C_{1} = 2 μF. \end{matrix}

A II. esetben az eredő ellenállás

\begin{matrix} X = r_{a} \frac{1 + {(ω C_{11} r_{b})}^{2}}{1 + {[ω C_{11} (r_{a} + r_{b})]}^{2}} . \end{matrix}

A táblázat alapján számolt valamely

(ω, X)

értékpárt ide helyettesítve kapjuk a kondenzátor kapacitásának ilyenkor érvényes nagyságát:

\begin{matrix} C_{11} = 0,5 μF \end{matrix}

III. kísérleti forduló

A feladat két folyadék elegye sűrűségének tanulmányozása volt a koncentrációtól való függésben. Ezután a felületi feszültségnek a koncentrációtól való függését kellett megvizsgálni.