Cím:	Az 1981. évi Arany Dániel matematikai tanulmányi verseny feladatai
Füzet:	1981/november, 97 - 99. oldal	PDF  |  MathML
Témakör(ök):	Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Kezdők (legfeljebb I. osztályosok) I. forduló   1. Valaki 1981-ben annyi éves, amennyi a születése éve számjegyeinek az összege. Mikor született? 2. Az $ABC$ derékszögű háromszög $AB$ átfogóján vegyük fel a $D$ és $E$ pontokat úgy, hogy $AC=AD$ és $BC=BE$ legyen. Határozzuk meg az $ECD\sphericalangle$-et! 3. Mely valós $x$-ekre teljesül a $\begin{array}{c}{\displaystyle \frac{2x+a}{3x+a}\ge 0}\end{array}$ egyenlőtlenség, amelyben $a<0$? 4. Az $ABC$ egyenlő szárú háromszög $AC$, ill. $BC$ szárára szerkesszünk $X$, ill. $Y$ pontokat úgy, hogy $AB\parallel XY$ és $XY=2AX=2BY$ teljesüljön. 5. Az $A$ és $B$ városból egyszerre indul egymással szemben két gépkocsi. Állandó sebességgel haladnak és $7$ óra $40$ perckor találkoznak. Az $A$-ból induló gépkocsi $11$ órakor érkezik $B$-be, a $B$-ből induló pedig $8$ óra $30$ perckor $A$-ba. Mikor indult a két gépkocsi? Mekkora a két gépkocsi sebességének az aránya? 6. Egy sakkversenyen négy játékos vett részt. Mindenki egyszer játszott mindenkivel. Egy-egy győzelemért $1$, döntetlenért $1/2$, vereségért $0$ pontot kaptak. Az első helyezett egyetlen játszmát sem vesztett el, a második nem játszott döntetlent, a harmadik egyetlen játszmát sem nyert. Állapítsuk meg minden egyes játszma eredményét, tudva azt, hogy minden versenyző végső összpontszáma különböző volt. 7. Az $ABC$ derékszögű háromszög köré rajzoljunk négyzetet a mellékelt ábra szerint $\left(DA=AC;DE\parallel CB\right)$. Igazoljuk, hogy az $AF$, $BD$, $CG$ egyenesek egy pontban metszik egymást. 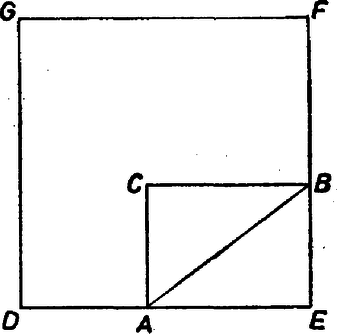8. Határozzuk meg az összes olyan $x$, $y$, $n$ pozitív egész számhármast, amelyben $x$ és $y$ a tízes számrendszerben egyaránt $n$-jegyű és $x^2=y^3$.   Kezdők, II. forduló   Szakközépiskolások feladatai   1. A lakásom és az iskola közötti utat tízszer gyorsabban teszem meg autóval, mint gyalog. Ha ennek az útnak az egyharmadát gyalog, a többit pedig autóval tenném meg, akkor ehhez $24$ percre volna szükségem. Az út hányad részét tettem meg gyalog, ha $9$ perccel hosszabb ideig közlekedtem, mintha csak autóval utaztam volna? 2. Egy háromszög kerülete $19$ cm, oldalainak hossza egész számokkal fejezhető ki, és egyik oldalának a hossza a másik kettő szorzatával egyenlő. Mekkorák a háromszög oldalai? 3. András, Béla és Csaba társasjátékot játszanak. Abban egyeznek meg, hogy aki elveszít egy játszmát, az megkétszerezi a másik kettő zsetonjainak számát. Három játszmát játszanak, s mindegyikük egyet veszít el. A játék végén Andrásnak és Bélának ugyanannyi zsetonja volt, míg Csabának egyetlen zsetonja sem maradt. Hány zsetonjuk lehetett külön-külön a játék kezdetekor, ha tudjuk, hogy hármójuknak összesen nem volt $20$ zsetonjuk, és mindegyiküknek egész számú zsetonja volt?   Általános tantervi osztályok feladatai   1. Keressük meg az összes olyan természetes számot, amely a tízes számrendszerben négyjegyű, jegyei rendre $a$, $b$, $c$, $d$; továbbá $a\cdot b=c+d$, $b\cdot d=a+c$ és $a\cdot c\cdot d={\left(a+d\right)}^3$. 2. Szerkesszünk egyenlő szárú háromszöget, ha adott a szárak által bezárt szög, továbbá a beírt és a körülírt kör középpontjának egymástól való távolsága. 3. Egy körmérkőzéses asztalitenisz bajnokságon $n$ játékos vett részt. A mérkőzések rendszertelenül kerültek sorra. Még nem volt vége a versenynek, amikor kiderült, hogy Péter, aki $k$ győzelmet aratott, behozhatatlan előnyre tett szert. Legalább hány mérkőzést játszottak le addig a bajnokságon?   Matematika II. tantervi osztályok feladatai   1. Keressük meg az összes olyan természetes számot, amely a tízes számrendszerben négyjegyű, jegyei rendre $a$, $b$, $c$, $d$; továbbá $a\cdot b=c+d$, $b\cdot d=a+c$ és $a\cdot c\cdot d={\left(a+d\right)}^3$. 2. Két egymásba nem nyúló $r$ sugarú kört tartalmazó egyenlő oldalú (szabályos) háromszögek közül melyiknek a területe minimális? 3. Egy $2n$ tagú társaságban $n^2$-nél több kézfogás történt. Tudjuk, hogy senki sem fogott többször kezet, mint András. Bizonyítsuk be, hogy azok között, akikkel András kezet fogott, van két olyan ember, akik egymással is kezet fogtak.   Haladók (legfeljebb II. osztályosok), I. forduló   1. Szerkesszük meg az egyenlő szárú háromszöget, ha adott az alapon fekvő szöge, valamint a magasságpontjának és súlypontjának távolsága. 2. Legyen $n$ tetszőleges természetes szám. Bizonyítsuk be, hogy a ${10}^n-1$ szám $37$-tel osztva négyzetszámot ad maradékul! 3. Az $ABC$ háromszög $P$ belső pontjára igaz, hogy $\begin{array}{c}{\displaystyle \frac{PBA\sphericalangle }{CBA\sphericalangle }=\frac{PAC\sphericalangle }{BAC\sphericalangle }=\frac{PCB\sphericalangle }{ACB\sphericalangle }=x\mathrm{.}}\end{array}$ Mennyi $x$ értéke ? 4. Mennyi az olyan hatjegyű számok összege, amelyeknek számjegyei között csak $1$-es vagy $2$-es szerepel? 5. Egy háromszög három csúcsa köré szerkesszünk páronként közös belső pont nélküli köröket úgy, hogy kerületük összege a lehető legnagyobb legyen! 6. Milyen esetben osztható hat szomszédos természetes szám négyzetének összege $7$-tel? 7. A síkon adott $200$ pont. Igazoljuk, hogy a pontokat ki lehet színezni pirossal és kékkel úgy, hogy $100$ piros pont legyen, $100$ kék, és akármelyik két piros pontot összekötő szakaszra igaz, hogy semelyik két kék pontot összekötő szakaszt sem metszi! 8. Egy négyszög belsejébe négy kör rajzolható úgy, hogy mindegyik csúcshoz tartozik egy kör, amely érinti az oda futó oldalakat és a szomszédos csúcsokhoz tartozó két kört. Bizonyítsuk be, hogy ha a négyszög érintőnégyszög, akkor deltoid is!   Haladók (II. forduló)   A szakközépiskolások feladatai   1. Legyenek $m$ és $n$ egymástól különböző természetes számok, amelyekre $n$ osztható $m$-mel. Tekintsük azon