Cím: Fixpont tételek (Fordította:Pataki János)
Szerző(k):  Vertgejm, B. 
Füzet: 1981/november, 107 - 112. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

(Megjelent a Kvant c. folyóirat 1980/6. számában)
 

Egyenletek megoldását keresve, jó tudni, létezik-e egyáltalán a megoldás ‐ egyébként ugyanis csak az időt vesztegetjük. A kérdés akkor válik igazán komollyá, ha meggondoljuk, hogy bonyolult egyenletek és egyenletrendszerek számítógépes megoldása értékes gépidőt emészthet fel. Ezért olyan fontosak az úgynevezett egzisztenciatételek, amelyek a megoldások létezését mondják ki. Ezek egyikét, a Brouwer-féle fixpont-tételt mutatjuk be az alábbiakban.
 

Séta
 

Közelünkben ketten sétálnak. Egyikük az A pontból halad B felé, a másik pedig eközben valahol A és B között bandukol. Találkozásuk nyilván elkerülhetetlen: legalább egy ízben egymás mellett lesznek.
Nézzük ezt kissé részletesebben (1. ábra).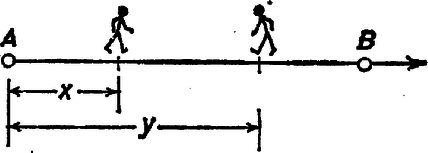
 

1. ábra
 

Jelölje x az első, y pedig a második sétáló távolságát az A ponttól. Ekkor az x minden értékének (vagyis az első sétáló bármely helyzetének) egyértelműen megfeleltethető egy y érték (a második sétáló helyzete ugyanebben a pillanatban), így az y=f(x) függvényt kapjuk. A találkozás helyét az
f(x)=x
egyenlet megoldása adja.
Legyen például AB=1000  m, y=100+0,6x. Ha x=0, akkor y=100; ha x=1000, vagyis az első már célhoz ért, akkor y=700. Megoldva a
100+0,6x=x
egyenletet, x=250  m adódik; itt hagyja el az első a másodikat.
Ha a második mozgása kevésbé egyszerű, akkor az f függvény ‐ és így az egyenlet megoldása is ‐ bonyolultabb, mindazonáltal nyilvánvaló, hogy legalább egy találkozás mindig létrejön. Ezzel a "nyilvánvalóval'' azonban csínján kell bánni. A továbbiakban egy feltételt fogalmazunk meg, majd bizonyítjuk, hogy e feltétel fennállása esetén a találkozás feltétlenül megtörténik.
Tegyük fel, hogy ‐ a példában tapasztaltaknak megfelelően ‐ az f függvény az [a;b] zárt intervallumot önmagába képezi le, vagyis ha x∈[a;b], akkor a≤f(x)≤b. Az f(x)=x egyenlet tetszőleges [a,b]-beli megoldását az f függvény fixpontjának nevezzük. (Példánkban ilyen fixpont a találkozás helye.)
 

Tétel: Ha az [a;b] zárt intervallumot önmagába leképező f függvény folytonos, akkor létezik fixpontja.
 

A tételben az f folytonossága és az intervallum zártsága egyaránt lényeges.
 

1. feladat. Mutassunk példát olyan nem folytonos f függvényre, amely az [a;b] intervallumot önmagába képezi le, de nincs fixpontja.
 

2. feladat. Mutassunk példát olyan folytonos függvényre, amelyik a) az [a;b]∪[c;d] halmazt; b) az (a;b) nyílt intervallumot önmagába képezi le, de nincs fixpontja.
 

A bizonyításhoz vezessük be a φ(x)=f(x)-x jelölést, ez a φ függvény folytonos. Világos, hogy c∈[a;b] pontosan akkor fixpontja f-nek, ha gyöke a φ(x)=f(x)-x=0 egyenletnek. Így a továbbiakban ennek az egyenletnek keressük megoldását. Vegyük észre, hogy az a≤x≤b, a≤f(x)≤b feltételekből φ(a)≥0 és φ(b)≤0 következik. Föltehető, hogy mindkét esetben egyenlőtlenség áll, hisz egyébként máris gyököt találtunk. Osszuk most tíz egyenlő részre az [a;b] intervallumot, és színezzük pirosra mindazokat a részintervallumokat, melyek bal oldali végpontjában φ pozitív, és kékre a többit. A legelső intervallum nyilván piros; haladjunk most balról jobbra mindaddig, míg elérjük az első kék intervallumot, illetve ha ilyen nincs, akkor az [a;b] intervallum végét. Legyen az utunk során érintett utolsó piros intervallum [a1;b1]. Ekkor φ(a1)>0 és φ(b1)≤0, így az eljárást kezdhetjük elölről. Tíz részre osztjuk [a1;b1]-et, a részeket kiszínezzük a fenti elv szerint, majd megkeressük azt az [a2;b2] részintervallumot, melyre φ(a2)>0, de φ(b2)≤0, és így tovább. Így a monoton növő, felülről korlátos
a≤a1≤a2≤...≤ak≤...<b.
sorozathoz jutunk. Ismeretes, hogy ilyen sorozatnak létezik határértéke, azaz van olyan c∈[a;b], melyre limk→∞ak=c.
Megmutatjuk, hogy φ(c)=0. Tegyük fel, hogy ez nem igaz, és legyen ε=12|φ(c)|>0. Ha most φ(c)<0 volna, akkor ‐ mivel φ(ak)>0, azért
|φ(c)-φ(ak)|>φ(c)>ε
minden k-ra. Másrészt mivel limk→∞ak=c és φ folytonos, így limk→∞φ(ak)=φ(c), tehát a |φ(c)-φ(ak)|>ε egyenlőtlenség nem teljesülhet minden k-ra. Hasonló ellentmondásra vezet a φ(c)>0 feltevés is a |φ(c)-φ(bn)|≥|φ(c)| egyenlőtlenség felhasználásával.
A fenti tétel alkalmazásával döntsük el, van-e gyöke a cosx3-x=0 egyenletnek! A cosx3 függvény folytonos, a [-π/2;π/2] intervallumot önmagába képezi le (a függvény értékei is ebbe az intervallumba esnek), így a tétel szerint létezik gyöke.
Vegyük észre, hogy az {ak} és a {bk} sorozatok a gyökhöz tartanak, és az [a;b] intervallumot tíz helyett akárhány részre is oszthatnánk. Ezt a módszert valóban alkalmazzák egyenletek közelítő megoldásainak kiszámítására.
Tételünk semmit sem mond a megoldások számáról; nyilván több fixpont is lehetséges.
 

Egy csésze kávé
 

Előttünk van egy csésze kávé. Egyenletesen kevergetve a csésze közepén a kávé mozdulatlan marad. Ha nem körbe keverjük, a kép kuszább lesz, de két különböző pillanatban megfigyelve a felszínt, mindig találunk olyan részecskét, amely helyben marad abban az értelemben, hogy mindkét pillanatban ‐ de persze nem az egész idő alatt ‐ ugyanazon a helyen van.
Ez fizikai meggondolások alapján nyilvánvaló, hiszen a súrlódás miatt a részecskék a csésze fala mellett nem mozdulnak el. Egyáltalán nem nyilvánvaló ‐ de igaz marad ‐ az állítás, ha csupán a változás folytonos voltát követeljük meg (tehát azt, hogy "közeli'' részecskék ne távolodjanak "túlságosan'' el egymástól).
A megfigyelt jelenség matematikai leírásához szükségünk van néhány fogalomra.
Legyen M egy ponthalmaz (az egyenesen, síkon vagy a térben); f pedig az M leképzése önmagába: vagyis az M halmaz minden x pontjára y=f(x)∈M. Egy ilyen leképezést folytonosnak nevezünk, ha minden x0∈M-hez és minden ε>0 számhoz létezik olyan (x0-tól és ε-tól függő) δ>0, hogy M minden olyan x pontjára, melyre x közelebb van x0-hoz, mint δ, a képeik, f(x) és f(x0) távolsága kisebb ε-nál.
Ha M a számegyenes részhalmaza, akkor x0 és x távolsága |x0-x|, a képeiké |f(x0)-f(x)|, így definíciónk a folytonos függvények ismert definíciójába megy át.
A korábbiaknak megfelelően az x∈M pontot az f függvény fixpontjának hívjuk, ha f(x)=x.
Mikor létezik az f leképzésének fixpontja ? A választ Luitzen Egbertus Jan Brouwer (1881‐1959) holland matematikus fixpont tétele adja meg. Ezt a nevezetes tételét nem is olyan régen, 1911-ben bizonyította. A tétel, nagyszámú általánosításával együtt, jelentős szerepet tölt be a modern matematikában. A fixpont tételek elméleti és gyakorlati szempontból egyaránt fontosak: a szárnyprofilok tervezésekor éppúgy használják őket, mint a különböző játékok optimális stratégiáinak és egyensúlyi helyzeteinek vizsgálatánál, valamint közgazdasági modellek készítésénél.
 

Brouwer tétele: A zárt körlap önmagára történő folytonos leképzésének létezik fixpontja.
 

A tétel nemcsak körlapra igaz, hanem minden olyan konvex, korlátos halmazra is, amely a határát tartalmazza: például téglalapra, háromszögre, illetve tetszőleges konvex sokszögre. A térben is teljesül például a kockára vagy a gömbre.
 

3. feladat. Mutassunk példát olyan síkbeli, korlátos M halmazra, és annak olyan önmagába történő folytonos leképezésére, melynek nincs fixpontja.
 

4. feladat. Mutassunk példát a nyílt körlemeznek olyan folytonos, önmagába történő leképezésére, melynek nincs fixpontja.
 

5. feladat. Mutassunk példát a zárt körlemez olyan nem folytonos leképezésére, melynek nincs fixpontja.
 

Brouwer tételét nem a fenti formában bizonyítjuk; csak azzal az esettel foglalkozunk, ha az M halmaz szabályos háromszög.
Az a oldalú ABC szabályos háromszögre építsük fel a 2. ábrán látható hálózatot.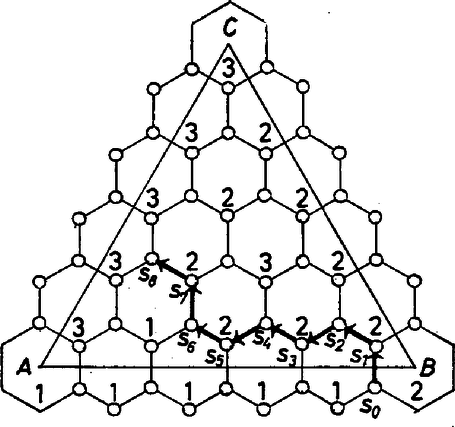
 

2. ábra
 

A háromszög belsejében levő, kis körökkel jelölt szögpontok mindegyikéből három él indul ki, ezek az élek a szomszédos szögpontokat kötik össze. A hálózat "sejtjei'' b oldalú szabályos hatszögek. A háromszög oldalait k egyenlő részre osztó pontok, valamint a háromszög csúcsai a határolósejtek középpontjai. Nyilván k⋅b⋅3=a, a sejtek száma pedig (k+1)(k+2)/2. Minden belső szögpont három, a határon levő pedig kettő vagy egy sejthez tartozik.Számozzuk meg a sejteket az 1, 2, 3 számokkal a következő módon: az AB oldalon levő, B-t nem tartalmazó határolósejtek kapják az 1-es számot; a BC oldalon lévő, C-t nem tartalmazók a 2-t, a megmaradt határolósejtek pedig 3-asok. A belső hatszögekbe a számokat tetszőleges módon írhatjuk (2. ábra). Egy szögpontot telített pontnak nevezünk, ha 1-es, 2-es és 3-as sejtnek is csúcsa. A most következő állítás az ún. Sperner-lemma speciális esete.1
 

Segédtétel: Létezik telített szögpont.
 

Bizonyítás. Felépítünk egy töröttvonalat 1-2 típusú, tehát 1-es és 2-es számú sejtek közös határán haladó élekből. A határon kezdjük, ahonnan a számozás miatt indul ilyen s0s1 él. Azt állítjuk, hogy ilyen éleken haladva véges számú lépés után telített pontba érünk. Ha ugyanis az 1-2 típusú sk-1sk él (k=1,2,...) sk végpontja nem telített, akkor található olyan sksk+l él, melyre sk+l≠sk-1 és amelyik ugyancsak 1-2 típusú (3. á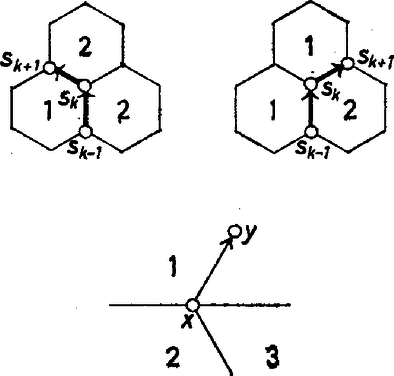bra).
 

3‐4. ábra
 

Az út nem juthat ki a határra és nem térhet vissza önmagába sem (miért?). A csúcsok száma viszont véges, így a töröttvonal feltétlenül telített pontba torkollik.
 

A hattyú, a rák és a csuka
 

Készen állunk Brouwer tételének bizonyítására, amennyiben az M halmaz az ABC szabályos háromszög. Osszuk fel a háromszög oldalait k egyenlő részre, készítsük el a 2. ábrán látható sejthálózatot, és a határolósejteket számozzuk meg az előbbi módon. Ezek után egy belső sejt számát a következőképpen határozzuk meg. Jelöljük a sejt középpontját x-szel. Ha x távolsága AB-től nem nagyobb, mint f(x)-é (az x pont nem "süllyed'' a leképzés hatására), akkor a sejt az 1 számot kapja. Ha x nem ilyen, ámde x nem közeledik BC-hez (x távolsága BC-től nem nagyobb, mint f(x)-é), akkor a sejt a 2 számot kapja. A megmaradó sejtek 3-asok lesznek, ezek középpontjai a leképezés hatására CA-tól eltávolodnak. A 4. ábrán az x középpontú sejt aszerint kapja az 1, 2, 3 számok valamelyikét, hogy az xy→ vektor melyik tartományba mutat.
Segédtételünk szerint a szögpontok között létezik telített pont, jelöljük ezt (vagy ha több van, az egyiket) xk-val. Az előálló helyzetet Krilov verse szemlélteti:
 

A Hattyú, a Csuka meg a Rák
 
Egyszer a Hattyú a Csukával és a Rákkal
Akart elhúzni egy tele kocsit;
Nos hát, befogtak, s indulnának végre,
Majd megfeszül mind: húz, vontat, szorít ‐
Ám a kocsi, bár könnyű volt, nem mozdul mégse,
Mert a Hattyú felfele tört az égre,
A Rák meg hátra ‐ s vízhez a Csuka.
Ne firtassuk itt, ki volt az oka:
De a kocsi nem indult el soha.
 

Mándy Stefánia fordítása
 

A versbeli szekérhez hasonlóan húzzák háromfelé xk-t a vele összefüggő sejtek. Ez a pont már majdnem fixpont, hiszen elegendően kis sejtméret esetén csak keveset közeledhet AB-hez, BC-hez és CA-hoz is ‐ vagyis alig mozdul el.
Nézzük most a telített szögpontokból álló {xk} sorozatot.
Első eset. Az {xk} sorozat konvergens.1 Tartson a sorozat az x ponthoz, ekkor x az adott leképzés fixpontja. (Ez következik az f leképzés folytonosságából, emiatt ugyanis x a háromszög egyik oldalához sem közeledhet.)
 

6. feladat. Bizonyítsuk be, hogy x valóban fixpont.
 

Második eset. Az {xk} sorozat nem konvergens. Ebben az esetben megadható a természetes számokból álló k1<k2<...<kn... sorozat úgy, hogy {xk}-nak az xk1,xk2,...,xkn,... részsorozata már konvergens. Legyen limn→∞xkn=x', ekkor x' fixpont.
 

7. feladat. Bizonyítsuk be a fenti tulajdonságú részsorozat létezését és azt is, hogy x' fixpont.
 

A fixpont-tételek fejlődése
 

Brouwer fixpont-tétele, amelyet zárt intervallumra és szabályos háromszögre igazoltunk, nemcsak a három, hanem a magasabb dimenziós terekben is igaz. Mi több, Schauder, lengyel matematikus megmutatta, hogy a tétel igaz "végtelen'' dimenziós terekben is. A témakör lényegesen gazdagodott Tyihonov szovjet és Banach lengyel matematikus munkássága nyomán. A legutóbbi időben pedig nagyteljesítményű elektronikus számítógépeket használnak a különböző feladatok megoldásait szolgáltató fixpontok keresésére.
 

8. feladat. A Brouwer-tétel zárt intervallumokra vonatkozó állításának felhasználásával mutassuk meg, hogy az
a)x-cosx=0;b)cos(sinx)-x=0
egyenleteknek létezik megoldása.
 

9. feladat. Az f:(x,y)→(x',y') leképezésnek, ahol x'=x2+1,5xy, y'=0,5xy+y2, van fixpontja az S={(x,y):x≥0;y≥0;x+y=1} halmazon. Bizonyítsuk be ezt az állítást Brouwer tételének felhasználásával, és oldjuk meg a megfelelő
x=x2+1,5xyy=0,5xy+y2


egyenletrendszert.
 

10. feladat. Igazoljuk, hogy az
x=sin(x+y)y=0,5(x2+xy3)


egyenletrendszernek létezik megoldása.
 

11. feladat. Van-e az alábbi egyenletrendszernek az x1=x2=x3=0 triviálistól különböző megoldása? Ha igen, keressük ezt meg!
x1=x22+2x2x3+x1x2x2=x32+x3x1x3=x12+x1(x2+x3)

B. Vertgejm
(Fordította: Pataki János)
1Sperner-lemmának a következő állítást szokás nevezni: Ha az AB oldalon levő határsejtek mindegyike 1-es vagy 2-es; a BC oldalon levők mindegyike 2-es vagy 3-as; a CA oldalon levők mindegyike pedig 3-as vagy 1-es, akkor létezik telített szögpont. Az itt szereplő segédtétel bizonyítása, a határsejtek speciális számozása miatt, lényegesen egyszerűbb, mint a Sperner-lemma bizonyítása. ‐ A szerk.

1Azt mondjuk, hogy egy pontsorozat konvergens, ha a pontok koordinátáiból alkotott számsorozatok konvergensek.