Kezdőlap


Cím:	Megjegyzések az F.2307. feladathoz
Szerző(k):	Bakos Tibor
Füzet:	1981/október, 53 - 58. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük az alaplap (szabályos ötszög) csúcsait rendre $A$ , $B$ , $C$ , $D$ , $E$ -vel, a gúla hatodik csúcsát $F$ fel. Mivel az oldallapok leforgatásával szabályos csillagötszög keletkezik, azért $F$ -nek az $A E$ él körüli leforgatott helyzete az $A B$ és $E D$ oldalegyenesek metszéspontjába esik (1. ábra).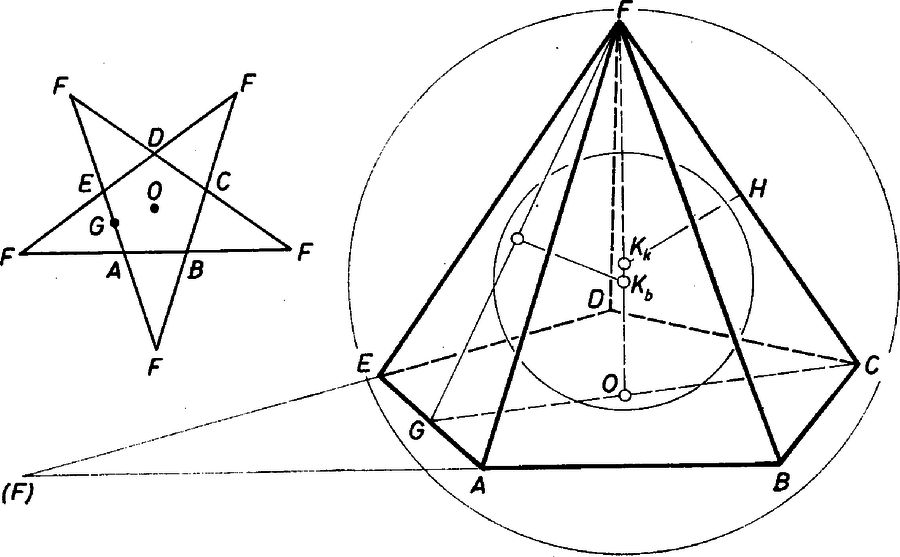

1. ábra

E szerint az oldallapok olyan egyenlő szárú háromszögek, amelyekben az alapon levő szög

72^{\circ}

, és az oldalélek hossza

\begin{matrix} A F = \frac{A E / 2}{cos F A E ∢} = \frac{1}{2 cos 72^{\circ}} = \frac{1}{2 sin 18^{\circ}} = \frac{2}{\sqrt[]{5} - 1} = \frac{\sqrt[]{5} + 1}{2} (= 1,618 egység) . \end{matrix}

Jelöljük az alaplap középpontját

O

-val ‐ ez a magasság talppontja ‐, az

A E

él felezőpontját

G

-vel. A gúla előírt szabályosságából következik, hogy mindkét gömb középpontja az

F O

magasságvonalon (forgási szimmetriatengelyen) lesz, továbbá a beírt gömb az alaplapot

O

-ban érinti, az

A E F

lapot pedig a

G F

oldalmagasság egy pontjában.
Legyen még a beírt gömb középpontja

K_{b}

, és sugara

ϱ

, így

K G_{b}

felezi az

F G O ∢ = γ

szöget, és

\begin{matrix} ϱ = O K_{b} = G O tg \frac{γ}{2} = G O \sqrt[]{\frac{1 - cos γ}{1 + cos γ}} . \end{matrix}

Itt ismert goniometriai összefüggések alapján, valamint felhasználva

18^{\circ}

-nak és többszöröseinek a szabályos ötszögből kiszámítható szögfüggvényeit, egyrészt

\begin{matrix} G O = A G tg 54^{\circ} = \frac{1}{2} \sqrt[]{\frac{5 + 2 \sqrt[]{5}}{5}} = \frac{1}{2} \sqrt[]{1 + \frac{2}{\sqrt[]{5}}}, \end{matrix}

másrészt

cos γ = G O / G F

, így a gyökjel alatti kifejezés:

\begin{matrix} \frac{1 - cos γ}{1 + cos γ} = \frac{G F - G O}{G F + G O} = \frac{G A (tg 72^{\circ} - tg 54^{\circ})}{G A (tg 72^{\circ} + tg 54^{\circ})} = \frac{sin 18^{\circ}}{sin 3 \cdot 18^{\circ}} = \frac{1}{3 - 4 sin^{2} 18^{\circ}} \\ = \frac{2}{3 + \sqrt[]{5}} = \frac{3 - \sqrt[]{5}}{2} . \end{matrix}

Ezekkel

\begin{matrix} ϱ = \frac{1}{2} \sqrt[]{\frac{5 + 2 \sqrt[]{5}}{5}} \cdot \frac{3 - \sqrt[]{5}}{2} = \sqrt[]{\frac{5 + \sqrt[]{5}}{40}} (= 0,4253 egység) . \end{matrix}

A körülírt gömb

R

sugarának számításához a

C O F

háromszöget használjuk. Jelöljük a gömb középpontját

K_{k}

-val,

F C

felezőpontját

H

-val. Az

F K_{k} H

és

F C O

derékszögű háromszögek hasonlóságából

\begin{matrix} \frac{F H}{R} = \frac{F O}{F C}, R = \frac{F C^{2}}{2 \cdot F O} = \frac{F C^{2}}{2 \sqrt[]{F C^{2} - O C^{2}}} . \end{matrix}

Itt

\begin{matrix} O C = O A = \frac{A G}{cos 54^{\circ}} = \frac{1}{2 sin 36^{\circ}} = \frac{2}{\sqrt[]{10 - 2 \sqrt[]{5}}} = \sqrt[]{\frac{5 + \sqrt[]{5}}{10}} . \end{matrix}

A nevezőbeli négyzetgyökjel alatt

\begin{matrix} F C^{2} - O C^{2} = {(\frac{\sqrt[]{5} + 1}{2})}^{2} - \frac{5 + \sqrt[]{5}}{10} = \frac{1}{5 - 2 \sqrt[]{5}} \end{matrix}

áll, végeredményben tehát

\begin{matrix} R = \frac{1}{4} \sqrt[]{10 + 2 \sqrt[]{5}} (= 0,9511 egység) . \end{matrix}

Megjegyzés. Két észrevételt teszünk számításaink alapján. Egyrészt

R / ϱ = \sqrt[]{5}

, másrészt

\begin{matrix} F O = \frac{F C^{2}}{2 R} = \sqrt[]{1 + \frac{2}{\sqrt[]{5}}} = R + ϱ, \end{matrix}

tehát

K_{b}

és

K_{k}

egybeesik.

II. megoldás (vázlat). Induljunk ki a szabályos ötszög eukleidészi szerkesztéséből (2. ábra).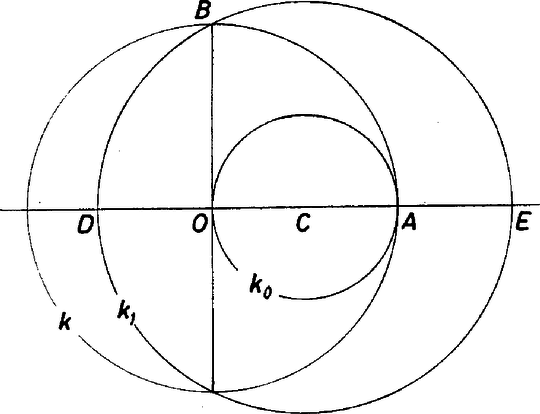

2. ábra

Legyenek

O A

és

O B

k

kör merőleges sugarai,

C

O A

szakasz felezőpontja, és jelöljük a

C

középpontú,

A

-n, illetve

B

-n átmenő köröket

k_{0}

-lal, illetve

k_{1}

-gyel,

k_{1}

-nek az

O A

egyenesen levő pontjait

D

-vel,

E

-vel (

D

legyen közülük

O

-hoz közelebb). Az

E B D

derékszögű háromszögben

B O

D O

O E = O A + A E = O B + D O

szakaszok mértani közepe, emiatt

\begin{matrix} D O : O B = O B : (O B + D O), \end{matrix}

vagyis

D O

és

O B

aránya megegyezik a szabályos tízszög oldalainak és a köré írt kör sugarának az arányával. Így

D O

valóban a

k

-ba írt szabályos tízszög oldala, és

\begin{matrix} B E^{2} = D E \cdot O E \end{matrix}

miatt

B E

k

-ba írt szabályos ötszög átlója, végül

D B : B E = D O : O B

miatt

D B

k

-ba írt szabályos ötszög oldala.
Forgassuk meg ezt az ábrát a

D E

egyenes körül, és jelöljük a

k_{0}

k_{1}

körök forgatásából keletkező gömböket

G_{0}

lal,

G_{1}

-gyel.

G_{1}

-ből a

B O

forgatásából származó sík

k

-val egybevágó kört metsz ki, tehát az ebbe írt szabályos ötszög oldalai

B D

-vel egyenlőek, átlói pedig

B E

-vel. így ez az ötszög

E

-vel együtt épp a feladatban szereplő gúlát határozza meg, ha

B D

egységnyi.
A kapott gúlának

G_{1}

természetesen a köré írt gömbje, megmutatjuk, hogy

G_{0}

a beírt gömb. A konstrukció miatt

G_{0}

érinti az alaplapot, melyben például a

B

csúcsból induló átlók az oldallapokkal egybevágó háromszögeket zárnak közre. Mivel

B C = E C

, a

G_{0}

-hoz

E

-ből húzott érintősíkok is

k

-val egybevágó köröket metszenek ki

G_{1}

-ből, tehát a gúla oldallapjai valóban érintik

G_{0}

-t.
Ha

O C = ϱ

, akkor

B C = ϱ \sqrt[]{5}, D O = ϱ (\sqrt[]{5} - 1), D B^{2} = ϱ^{2} (10 - 2 \sqrt[]{5})

. Ha tehát

D B = 1

, akkor

\begin{matrix} ϱ^{2} = \frac{1}{2} \frac{1}{5 - \sqrt[]{5}} = \frac{5 + \sqrt[]{5}}{40} . \end{matrix}

Így a gúlába írt gömb sugara

ϱ = \sqrt[]{\frac{5 + \sqrt[]{5}}{40}}

és a gúla köré írt gömb sugara

B C = ϱ \sqrt[]{5} = \sqrt[]{\frac{5 + \sqrt[]{5}}{8}}

MEGJEGYZÉSEK

1. Az I. megoldás számításaira támaszkodva kapcsolatot írunk le gúlánk, a szabályos dodekaéder, valamint az utóbbinak magasabb fajú rokonai között.
Az

F O

és

G O

szakaszok kifejezései alapján a gúla alapéleinél keletkező lapszögekre

tg F G O ∢ = 2, cos F G O ∢ = 1 / \sqrt[]{5}

. Ez azt jelenti ‐ mint alább megmutatjuk ‐, hogy az oldallapok által a kiterítés közben ,,súrolt''

F G (F)

nagyságú lapszögek egyenlők a szabályosan dodekaéder szomszédos lapjai közti szögekkel (lásd a megoldás 1. ábráját). Ha tehát az egységnyi élű dodekaéder lapjaira 1‐1 példányt illesztünk a vizsgált gúlából ‐ természetesen az alapötszögüknél fogva ‐, akkor az

A B C D E = L

dodekaéderlapra állított gúla

E A F

oldallapja olybá vehető, mintha a szomszédos

A E D_{1} C_{1} B_{1} = L_{1}

dodekaéderlapra állított gúla

E A F_{1}

oldallapjának lenne a kiterítése az

L_{1}

alapsíkba (az

1

-es index az

A E O^{*}

síkra való tükörképet jelöli, ahol

O^{*}

a dodekaéder középpontja). Ugyanez áll a

12

gúla együttvéve

60

oldallapjára (1 . és 2. ábra a borító hátoldalán).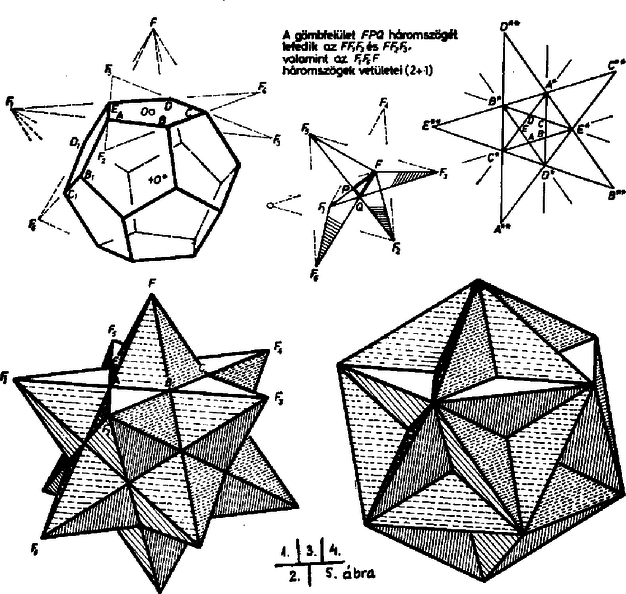

Azt is mondhatjuk tehát ‐ a gúlákat mellőzve ‐ , hogy amit látunk, az a dodekaéder lapjaiból kiterjesztéssel keletkezett

12

csillagötszöglap együttese (2. ábra, egyező csíkozás-színezés az egy-egy csillaglapot alkotó 5‐5 részen).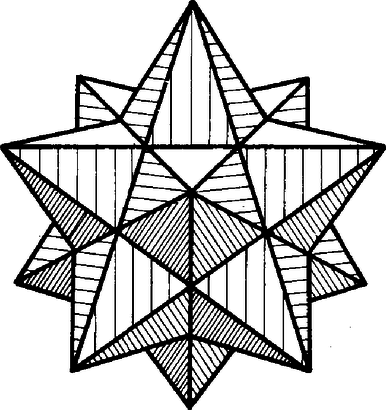

És ezzel előttünk áll egyike a 4, ún. Poinsot-féle (olvasd: poenzo) magasabb fajú szabályos poliédernek. A lapok

5

-ösével új csúcsot alkotnak,

2

-esével élben metszik egymást (gúlacsúcstól gúlacsúcsig, az eredeti dodekaéder csúcsai már nem számítanak csúcsnak). Az új

12

csúcs ,,kis környezetei'' konvex testszögletek.
Ezt a problémakört L. Poinsot (1777-1859) francia matematikus-fizikusnak egy, a szabályos csillagsokszögekről kimondott, algebrai jellegű állítására támaszkodva A. Cauchy dolgozta ki először. A csillagötszöglapokat másodfajúnak mondják, és ezen azt értik, hogy mialatt egy mozgó pont a megoldás 1. ábrájának bal felső

F

-jéből

G

-n át az alsó

F

-be megy, majd

C

-n át a jobb felsőbe,

E

-n át a bal alsóba,

B

-n át a jobb alsóba, végül

D

-n át visszatér, eközben a körülírt körön

O

-ból való vetítéssel előálló ,,vetülete'' kétszer járja körül a kört. Másképpen: a csillagötszög oldalainak

O

-ból való vetületei kétszeresen fedik le a kört.
Hasonlóan, ha vetítjük az új poliéder

12

db csillagötszög lapját

O^{*}

-ból egy, az

O^{*}

körüli gömbfelületre, a vetületek

3

-szorosan fedik le a gömböt. Erre utal új poliéderünk másik jelzője: harmadfajú (a borító 3. ábrája).

Szemléletesen azt mondjuk, hogy a harmadfajú, csillaglapú, konvexcsúcsú szabályos dodekaéder

12

csúcsának konvex burka szabályos ikozaéder.
2. További kettőt kapunk meg a Poinsot-poliéderek együtteséből a 4. ábra kiterjesztési terve szerint. Ez annak a

10

metszésvonalnak az együttese, amelyekben a közönséges szabályos dodekaéder egy lapjának síkját a többi lapsíkok metszik (

1

lap nem metszi, hiszen a

12

lap páronként párhuzamos). Tekintsük a belső kis konvex ötszöget felső lapnak, ennek oldalegyeneseit a vele szomszédos ‐ a ,,felső kis kosarat'' alkotó ‐ lapok síkjai metszik ki, a nagyobbik csillagötszög oldalegyeneseit pedig az alsó kosár

5

lapjának síkjai.
Az első újabb poliédert úgy kapjuk, hogy az

A B C D E

lapot az

A^{*} B^{*} C^{*} D^{*} E^{*}

konvex ötszög kerületéig terjesz tjük ki (az első kiterjesztés az

A^{*} C^{*} E^{*} B^{*} D^{*}

csillagötszögre történt), és ugyanezt végezzük a dodekaéder mindegyik lapján (5. ábra). A lapok most (ismét) elsőfajúak, a csúcsok a legutóbbiak, de a ,,kis környezetük'' nem konvex, hanem csillag alapú testszöglet. Új élek jelentek meg, az eddigiek pedig eltűntek, pl. az

A^{*} C^{*}

egyenes most nem él, mert nem határvonala lapnak. (Ahogyan a síkban pl.

A

nem csúcs, amikor

B^{*} D^{*}

-ot tekintjük élnek.) Ez a poliéder a harmadfajú, konvex lapú, csillagcsúcsú szabályos dodekaéder.
Szemléletesen: a konvex burok még mindig az előbbi ikozaéder, de már nemcsak a csúcsait örökölte az új poliéder, hanem az éleit is; a lapjai helyén viszont kis gúlaszerű gödrök, völgyek alakultak ki az újabb lapkiterjesztésekből (6. ábra).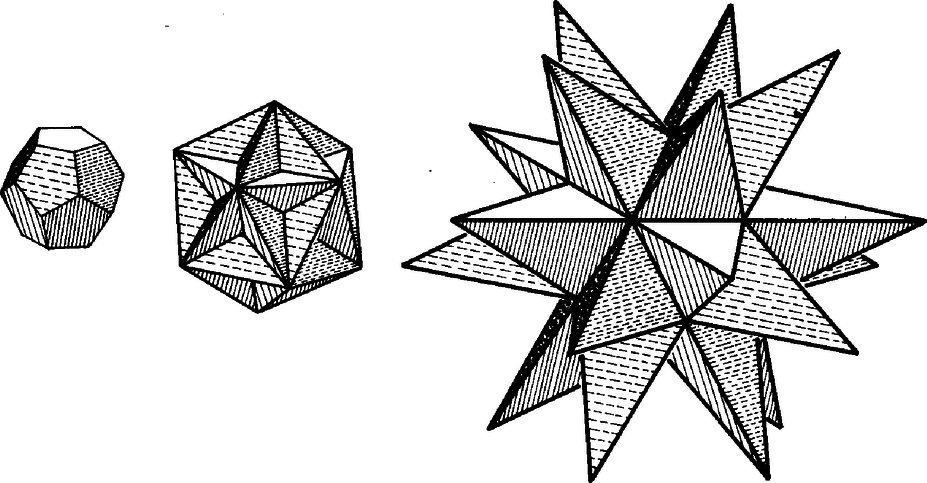

6. ábra

Végül az

L

lap (és minden lap) lehető legnagyobb kiterjesztésével az

A^{* *} C^{* *} E^{* *} B^{* *} D^{* *} (A^{* *})

csillagötszöglaphoz jutunk, ennek éleihez az alsó kosár lapjainak ugyanígy kiterjesztett lapjai csatlakoznak (6. ábra). A

12 \cdot 5 = 60

ék alakú kiterjesztési részháromszög

3

-asával

20

új csúcsot alkot, és mintegy

3

-oldalú gúlákkal fedik be az előbb említett völgyeket. Az élek ismét újak. Ez a poliéder a

7

-edfajú, csillaglapú, konvex csúcsú szabályos dodekaéder. Konvex burka szabályos dodekaéder.

A 4-féle szabályos dodekaéder jellemzői

\begin{matrix} A lapok & A csúcsok & A poli- \\ alakja & faja & száma & alakja & összefutó & faja & éder faja \\ élek száma \\ Közönséges dodekaéder & konvex & 1 & 20 & konvex & 3 & 1 & 1 \\ 1. kiterjesztés & csillag & 2 & 12 & konvex & 5 & 1 & 3 \\ 2. kiterjesztés & konvex & 1 & 12 & csillag & 5 & 2 & 3 \\ 3. kiterjesztés & csillag & 2 & 20 & konvex & 3 & 1 & 7 \end{matrix}

A fentiekben csupán szemléletesen írtuk le ezt a

3

poliédert, a család negyedik tagjával nem is foglalkoztunk, mert az a közönséges ikozaéderből fejlődik ki. Persze azt sem bizonyítják a fentiek, hogy más ilyen poliéder nem létezik.
3. A dodekaéderlapok közti szöget a Gy. 1757-ben is használt szerkesztő eljárásra^{$^{*}$} támaszkodva számítjuk ki (7. ábra).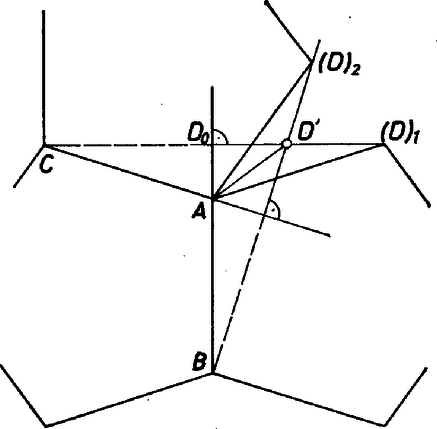

7. ábra

A

csúcsba összefutó

3

lap által alkotott testszöglet

A D

élét felvágjuk és a

D A B

D A C

lapot az

A B

, ill.

A C

él körül beleforgatjuk az

A B C

lap síkjába. Ott az élek közti szögek valódi nagyságban látszanak. Majd ismét felhajtjuk a lapokat és a vetületükben kísérjük az újra egyesülő

D

pontok útját.
Legyen

{(D)}_{1}

vetülete

A B

-re

D_{0}

, így

D

{(D)}_{1} D_{0}

egyenes fölött fordul vissza, hasonlóan a másik a

{(D)}_{2}

-n átmenő,

A C

-re merőleges egyenes fölött, és e kettő metszése adja meg

D

-nek

D'

vetületét. Az

A D'

szakasz felezi az

A {(D)}_{1}

és

A {(D)}_{2}

közti szöget, így

D' A D_{0} ∢ = 54^{\circ}

, másrészt

{(D)}_{1} A D_{0} ∢ = 72^{\circ}

, ennélfogva

cos D D_{0} D' ∢ = D' D_{0} / D D_{0} = tg54^{\circ}/ tg72^{\circ}=1/\sqrt[]{5}

, amint állítottuk.

^{$^{*}$}K. M. L. 57 (1978) 140. o.