Cím:	1980. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldása
Szerző(k):	Surányi János
Füzet:	1981/február, 50 - 61. oldal	PDF  |  MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az 1980. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldása   1. feladat. A tér pontjait kiszínezzük $5$ színnel (mind az $5$ szín ténylegesen előfordul). Bizonyítsuk be, hogy van olyan sík, amelyik legalább $4$ különböző színű pontot tartalmaz.   Megoldás. A színeket nevezzük $a$, $b$, $c$, $d$, $e$-nek, és $A$, $B$, $C$, $D$, $E$ jelentsen a továbbiakban mindig egy‐egy $a$, $b$, $c$, $d$, ill. $e$ színű pontot. Egy egyenest, síkot, ha van rajta 3, 4, ill. 5 különböző színű pont, röviden 3-, 4-, ill. 5-színűnek fogunk nevezni. A megoldásokban gyakran fogunk használni két okoskodást, ezeket segédtételként előrebocsátjuk.   1. SEGÉDTÉTEL. Ha a feladat feltételei teljesülnek, és van egy $3$-színű egyenes, akkor van a térben $4$-színű sík. Valóban legyen a $v$ egyenesen mondjuk $a$, $b$ és $c$ színű pont is. Feltétel szerint van a térben $d$ színű $D$ pont; van továbbá olyan sík, amely tartalmazza $v$-t és $D$-t is, egy ilyen sík pedig (legalább) 4-színű.   2. SEGÉDTÉTEL. Ha a feladat feltételei teljesülnek, továbbá egy $3$-színű síknak és egy olyan egyenesnek, amelyiken van a maradó $2$ színű pont, van közös pontja, akkor van a térben $4$-színű sík.   Bizonyítás: Legyen az $S$ síkon $a$, $b$ és $c$ színű pont, a $v$ egyenesen $d$ és $e$ színű pont és $P$ legyen a sík és az egyenes közös pontja. Ha $P$ színe $a$, $b$ vagy $c$, akkor $v$ 3-színű, és így az 1. segédtétel szerint igaz az állítás; ha pedig $P$ $d$ vagy $e$ színű, akkor $S$ 4-színű. I. megoldás. Ha $A$, $B$, $C$, $D$, $E$ közül valamelyik négyen át fektethető sík, akkor igaz a feladat állítása. Ha nem, akkor tekintsük az $ABCD$ tetraéder oldallapjainak a síkját. Ha valamelyiknek, pl. a $B$, $C$, $D$ pontokat tartalmazó $S$ síknak ellenkező oldalára esik a tetraéder és $E$, akkor $AE$ metszi $S$-t (1/a 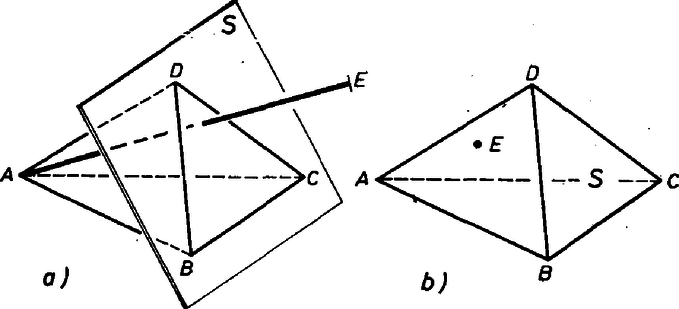ábra).   1. ábra   Ha viszont bármelyik síkot véve, annak ugyanarra az oldalára esik a tetraéder és $E$, akkor a tetraéder tartalmazza $E$-t (1/b ábra). $E$ különbözik $A$-tól, mert más színű, így közelebb van $S$-hez, mint $A$, tehát ez esetben is metszi $AE$ az $S$ síkot. Ekkor azonban a 2. segédtétel értelmében igaz a feladat állítása.   II. megoldás. Az $A$, $B$, $C$-t tartalmazó $S_1$ és $C$, $D$, $E$-t tartalmazó $S_2$ síknak van m metszésvonala, ha nem esnek egybe, mert van közös pontjuk, $C$. Ha a két sík egybeesik, akkor az 5-színű. Ha különbözők és $m$ tartalmaz $a$ vagy $b$ színű pontot, akkor $S_2$, ha pedig $d$ vagy $e$ színű pontot, akkor $S_1$ 4-színű.   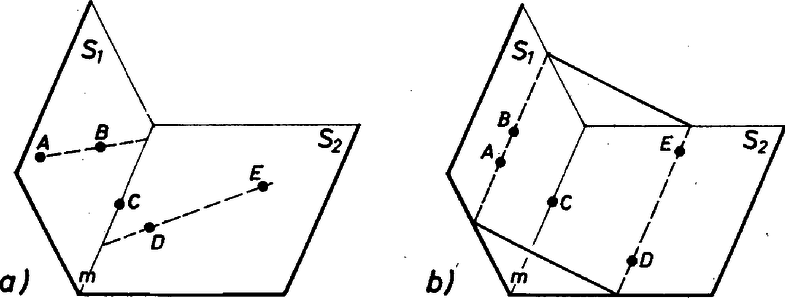2. ábra   Ha $m$ minden pontja $c$-színű, és $AB$ vagy $DE$ metszi $m$-et (2/a ábra), akkor a metsző egyenes 3-színű, és így az 1. segédtétel szerint igaz a feladat állítása. Ha végül $AB$ sem, $DE$ sem metszi $m$-et, akkor mindkettő párhuzamos $m$-mel (2/b ábra), mert $AB$-t és $m$-et az $S_1$, $DE$-t és $m$-et az $S_2$ sík tartalmazza, s így kitérők nem lehetnek. Ekkor azonban $AB$ és $DE$ is párhuzamos, így fektethető rajtuk át sík, és ez 4-színű. III. megoldás. Legyen $S$ az $A$-t, $B$-t és $C$-t tartalmazó sík. Ha ez 4-színű, akkor igaz a feladat állítása. Ha $S\text{'}$ 3-színű, de a $DE$ egyenes is 3-színű, vagy ha az egyenes metszi $S$-et, akkor az 1., ill. a 2. segédtétel szerint igaz a feladat állítása. Ha $S$ 3-színű, $DE$ 2-színű és $DE$ párhuzamos $S$-sel, akkor fektessünk síkot $A$-n, $D$-n és $E$-n át. Ez $S$-et egy $DE$-vel párhuzamos $m_a$ egyenesben metszi (3. ábra). 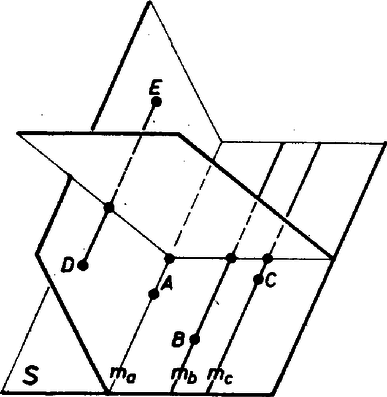  3. ábra   Ha $m_a$-n van $b$ vagy $c$ színű pont, akkor második síkunk 4-színű. Ha $m_a$ minden pontja $a$ színű és hasonlóan a $B$-n át $DE$-vel párhuzamosan húzott $m_b$ egyenes $b$ színű, a $C$-n át húzott $m_c$ párhuzamos pedig $c$ színű, akkor vegyünk egy $DE$-t metsző síkot. A metszéspont $d$ vagy $e$ színű, mert a $DE$ egyenes 2-színű. Ez a sík metszi a párhuzamos $m_a$, $m_b$, $m_c$ egyenest is, így 4-színű.   IV. megoldás. Ha van az $ABC$ síkot metsző, $d$ és $e$ színű ponton átmenő egyenes, akkor a 2. segédtétel szerint igaz a feladat állítása. Elég tehát azt az esetet vizsgálni, ha minden $e$ színű pont a $D$-n átmenő, $ABC$ síkkal párhuzamos síkban van. Ha hasonlóan a $BCD$ síkot és az $A$ ponton átmenő, $e$ színű pontot is tartalmazó egyeneseket vizsgáljuk, akkor tovább szűkíthetjük a megvizsgálandó eseteket arra, hogy az $e$ színű pontok legyenek rajta az $A$-n átmenő, $BCD$ síkkal párhuzamos síkon is. Hasonlóan folytatva tovább, megkívánhatjuk azt is, hogy a $B$-n átmenő, $ACD$ síkkal párhuzamos síkon is, valamint a $C$-n átmenő, $ABD$ síkkal párhuzamos síkon is legyenek rajta az $e$ színű pontok.   4. ábra   Ez a 4 sík azonban (az $ABCD$ tetraéderhez hasonló) tetraédert határoz meg (4. ábra), így nincs olyan pont, amelyik mindegyiken rajta lenne. Nem maradt tehát külön megvizsgálandó eset, s így mindig teljesül a feladat állítása. Eddig különböző színű pontokból indultunk ki. A következő megoldás éppen egyező színűeket keres.   V. megoldás. Kell lennie a térben 3 nem egy egyenesen levő, azonos színű pontnak, hiszen különben az egész térnek nem lehetne több, mint 5 egyenese. Legyenek az $A_1{A}_2{A}_3$ háromszög csúcsai $a$ színűek. Ha minden más színű pont a háromszög síkjában van, akkor ez a sík 5-színű. Ha nem, akkor legyen a síkon kívül egy $a$-tól különböző ‐ mondjuk $b$ színű ‐ pont $B$. A $B{A}_1$, $B{A}_2$, $B{A}_3$ egyenesek nincsenek egy síkban (5. ábra), tehát minden sík metsz legalább egy egyenest közölük. 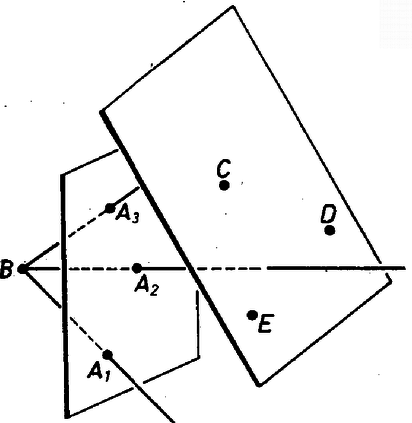  5. ábra   Egy‐egy $c$, $d$ és $e$ színű pontot véve, az ezeket tartalmazó sík tehát metszi a 3 egyenes valamelyikét, s így 2. segédtételünk alapján következik, hogy igaz a feladat állítása.   VI. megoldás. Megmutatjuk, hogy ha a tér pontjai úgy vannak megszínezve, hogy egy‐egy sík legfeljebb 3-színű, akkor a tér legfeljebb 4-színű. Megjegyezzük, hogy a feltételből következik, hogy a tér minden egyenese 2-színű, hiszen ha volna 3-színű egyenes, akkor a 2. segédtétel szerint volna 4-színű sík is. Ha 4 szín sem fordul elő, akkor nyilvánvalóan igaz az állításunk. Ha $A$, $B$, $C$, $D$ színe $a$, $b$, $c$, ill. $d$, akkor a 4 pont tetraédert határoz meg, hiszen nincs 4-színű sík. Legyen $P$ a tér tetszés szerinti pontja. Ha $P$ az $AB$ vagy a $CD$ egyenesen van, akkor az előrebocsátott megjegyzés szerint csak $a$ vagy $b$ színű, illetőleg csak $c$ vagy $d$ színű lehet. Ha egyik egyenesen sincs rajta, akkor a $P$-n, $A$-n és $B$-n átmenő $S_1$ sík és a $P$-n, $C$-n és $D$-n átmenő $S_2$ sík egyértelműen meg van határozva. Valamelyik síkot metszi a másikban levő tetraéderél egyenese, mert $AB$ és $CD$ kitérő, így mindegyiken át csak egy a másikkal párhuzamos sík fektethető, és az így keletkező két sík párhuzamos. $S_1$-nek és $S_2$-nek azonban közös pontja $P$, így nem lehetnek párhuzamosak (6. ábra).   6. ábra   Ha pl. $AB$ metszi $S_2$-t, a metszéspont $a$ vagy $b$ színű; a sík tartalmaz még $c$ és $d$ színű pontot, így $P$ színe is csak e 3 pont valamelyikével lehet egyező, mert $S_2$ is 3-színű. Nem fordulhat elő a tér pontjainak színe közt $a$, $b$, $c$ és $d$-től különböző. A bizonyított tételből következik, hogy ha a tér több, mint 4-színű, akkor van több, mint 3-színű sík, ez pedig éppen a bizonyítandó állítás.   Megjegyzések. 1. Volt, aki megmutatta, hogy 4-színű térnek nem feltétlenül van 4-színű síkja ‐ ami várható is ‐. A térben egyetlen $v$ egyenes pontjai legyenek $a$ és $b$ színűek, egy $v$-n átmenő $S$ sík $v$-n nem levő pontjai $c$ színűek és a tér $S$-en nem levő pontjai $d$ színűek (7. ábra). 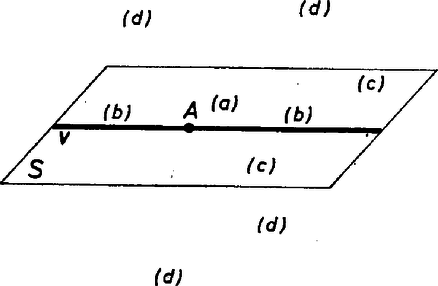  7. ábra   Itt csak a sem $S$-sel sem $v$-vel nem párhuzamos síkok lehetnének 4-színűek, ezek azonban $S$-et $c$ színű és vagy $a$ színű vagy $b$ színű pontokban metszik, de egyszerre mindhárom színűeket nem tartalmaznak. 2. Igaz és könnyen igazolható a feladat és az 1. megjegyzés állításának a síkbeli megfelelője: Ha egy sík pontjai 4 színnel vannak kiszínezve, akkor van olyan egyenes a síkban, amelyen előfordul 3 különböző színű pont. Ha viszont a sík minden egyenese 2-színű, akkor a sík legfeljebb 3-színű. Ezzel kapcsolatban felmerül a kérdés, hogy ha a sík pontjai csak 3 színnel vannak kiszínezve, de úgy, hogy minden színnel van színezve 3 nem egy egyenesen levő pont, vajon ebből nem kövekezik-e már 3-színű egyenes létezése. Meglepő, de A. W. Hales és E. Straus megmutatta, hogy ez nem következik. Ők megadtak olyan eljárást, amelynek segítségével úgy rendelhető a sík minden pontjához 3 szín valamelyike, hogy minden egyenes legfeljebb 2-színű legyen, de minden színhez legyen olyan háromszög, amelyiknek mindhárom csúcsa a megadott színű. Az eljárás túl bonyolult ahhoz, hogy itt ismertetni lehetne, csak azt említem meg érdekesség kedvéért, hogy kombinatorikus és számelméleti jellegű segédeszközök igen szellemes összekapcsolásával sikerül megadniuk egy kívánt tulajdonságú színezést. 3. Az egyik versenyző azt az érdekes kérdést vetette fel, hogy ha olyan 4-színű síkot keresünk, amelyiken egy előre kiválasztott szín előfordul, van-e ilyen is? Ő úgy látta, hogy nem föltétlenül található, de az általa megadott példa hibás, semmi nem derül ki belőle. A helyes válasz igenlő, hiszen van 4-színű sík a feladat állítása szerint és éppen említettük, hogy ezen van 3-színű egyenes. Legyen $v$-n $a$, $b$ és $c$ színű pont és legyen $D$ és $E$ $d$, ill. $e$ színű. Ekkor bármelyik színhez jó a $v$-t és $D$-t vagy a $v$-t és $E$-t tartalmazó sík. Síkban nem ez a helyzet. Legyenek egy $v$ egyenes pontjai $a$, $b$, $c$ színnel színezve, a sík többi pontjai pedig $d$ színűek. Ekkor $v$ az egyetlen 3-színű egyenes, $d$ színt tartalmazó 3-színű egyenes tehát nincs. Ha most folytatjuk a színezést a térre úgy, hogy a térnek az adott síkon kívüli pontjai mind legyenek $e$ színűek, akkor csak a $v$-n átmenő síkok négyszínűek a térben. Így nincs olyan négyszínű sík a térben, amin $d$ és $e$ szín is szerepelne. Ha tehát egy szín helyett színpárra ismételjük meg kérdésünket, akkor már a térben is tagadó a válasz.   2. feladat. Legyen $n>1$ páratlan egész szám. Bizonyítsuk be, hogy akkor és csak akkor léteznek olyan $x$, $y$ természetes számok, melyekre $\begin{array}{c}{\displaystyle \frac{4}{n}=\frac{1}{x}+\frac{1}{y}\mathrm{,}}\end{array}$ (1) ha $n$-nek van $4k-1$ alakú prímosztója.   I. megoldás. Tegyük fel, hogy van az egyenletnek pozitív egész $x$, $y$ megoldása. Legyen a két szám legnagyobb közös osztója $d$, azaz $\begin{array}{c}{\displaystyle x=d{x}_1\mathrm{,}y=d{y}_1\mathrm{,}}\end{array}$ ahol $x_1$ és $y_1$ pozitív egész és nincs 1-nél nagyobb közös osztójuk, más szóval relatív prímek. Ezt beírva az egyenletbe és a törteket eltávolítva, azt kapjuk, hogy $\begin{array}{c}{\displaystyle 4d{x}_1{y}_1=n\left(x_1+y_1\right)\mathrm{.}}\end{array}$ (2) Itt $n$ páratlan volta miatt a jobb oldal csak úgy lehet 4-gyel osztható, ha $x_1+y_1$ osztható 4-gyel. Ekkor $x_1$ és $y_1$ vagy mindkettő páros vagy mindkettő páratlan. Mivel ezen kívül relatív prímek is, csak a második eset következhet be. Minthogy pedig az összegük osztható 4-gyel, ez csak úgy lehet, ha az egyik $4k+1$ alakú, a másik $4k-1$ alakú. A (2) összefüggés szerint $x_1$ osztója az $n\left(x_1+y_1\right)$ szorzatnak. $x_1+y_1$-hez azonban relatív prím, hiszen ha volna 1-nél nagyobb közös osztójuk, az osztója volna $\left(x_1+y_1\right)-x_1=y_1$-nek is, azonban $x_1$ és $y_1$ relatív prímek. Ismeretes, hogy ebben az esetben $x_1$ csak úgy lehet osztója a szorzatnak, ha a másik tényezőjének, $n$-nek is osztója. Ugyanígy következik, hogy $y_1$ is osztója $n$-nek. Az $x_1$-re és $y_1$-re tett megállapításaink alapján következik, hogy ha megoldható az egyenlet, akkor van $n$-nek $4k-1$ alakú osztója. Ekkor azonban van ilyen alakú prímosztója is. Ha ugyanis egy $4k-1$ alakú számot akárhogy felbontunk tényezőkre, akkor azok közt van $4k-1$ alakú. Valóban, számunk páratlan, így a felbontás tényezői is páratlanok, akkor pedig vagy $4k+1$ vagy $4k-1$ alakúak. Két előbbi alakú szám szorzata is ilyen alakú: $\begin{array}{c}{\displaystyle \left(4k_1+1\right)\left(4k_2+1\right)=4\left(4k_1{k}_2+k_1+k_2\right)+\mathrm{1,}}\end{array}$ és ez az alak újabb ilyen tényezőkkel szorozva sem változik meg. Elő kell tehát fordulnia $4k-1$ alakúnak is. Ez igaz akkor is, ha prímtényezőkre bontottuk a számot. Így $n$ $4k-1$ alakú osztójának van $4k-1$ alakú prímosztója, de ez osztója $n$-nek is. Tegyük most fel, hogy $p=4k-1$ $n$-nek egy prímosztója: $n=p\cdot m$. Ekkor $\begin{array}{c}{\displaystyle \frac{4}{n}=\frac{4k}{k\cdot p\cdot m}=\frac{p+1}{k\cdot p\cdot m}=\frac{1}{km}+\frac{1}{kpm}\mathrm{,}}\end{array}$ tehát $x=km$, $y=kpm$ megoldása az egyenletnek. Ezzel a feladat állítását bebizonyítottuk.   Megjegyzések. 1. Felhasználtuk azt a tételt, hogy ha egy egész szám osztója egy szorzatnak, de annak egyik tényezőjéhez relatív prím, akkor osztója a másik tényezőnek. Ez következik a számelmélet alaptételéből, ami szerint minden 1-nél nagyobb természetes szám felbontható véges sok (pozitív) prímszám szorzatára és ez a felbontás a tényezők sorrendjétől eltekintve egyértelmű. Fordítva, az alaptétel is következik a fent kimondott tételből, az pedig bizonyítható az alaptétel felhasználása nélkül. 2. A bizonyítás befejező részében nem használtuk ki, hogy $p$ prím, tehát képleteink $n$ minden $4k-1$ alakú osztójához megadnak egy megoldást. 3. A megoldás első részének gondolatmenetét folytatva $n=n\text{'}{x}_1$ és $x_1$, $y_1$ relatív prím volta miatt a jobb oldali szorzat csak úgy lehet $y_1$-gyel osztható, ha $n\text{'}$ osztható vele: $n\text{'}=m{y}_1$. Ezeket beírva (2)-be $m\left(x_1+y_1\right)=4d$ adódik. Láttuk továbbá, hogy $x_1+y_1$ osztható 4-gyel, így $x_1+y_1=4e$ jelöléssel $\begin{array}{c}{\displaystyle \left(3_1\right)n=m{x}_1\left(4e-x_1\right)\mathrm{,}\left(3_2\right)x=em{x}_1\mathrm{,}\left(3_3\right)y=em\left(4e-x_1\right)\mathrm{.}}\end{array}$ Ebből is világos, hogy $x_1$ és $4e-x_1=y_1$ közül az egyik $4k+1$, a másik $4k-1$ alakú. Mivel $x$ és $y$ szerepe szimmetrikus, feltehetjük, hogy $x_1$ a $4k+1$ alakú. Tudjuk már, hogy $x_1$ és $4e-x_1$ relatív prímek. Azt kaptuk tehát, hogy az (1) egyenlet összes megoldását megkapjuk, ha vesszük $n$-nek $\left(3_1\right)$ alakú felbontásait, amelyekben $x_1$ és $4e-x_1$ relatív prímek, és képezzük hozzájuk a $\left(3_2\right)$, $\left(3_3\right)$ képletek szerinti értékeket, továbbá a két szám felcserélésével keletkező számpárt. $x$ és $y$ mindig különböző, mert $x_1$ és $4e-x_1$ nem lehet egyenlő. $n$-nek minden $t=4j-1$ alakú osztójához van legalább egy $\left(3_1\right)$ alakú felbontása. Válasszuk ugyanis $t-t$ $4e-x_1$-nek, $x_1$-nek pedig az $n/t$ bármelyik $4k+1$ alakú és $t$-hez relatív prím osztóját (az 1 mindig ilyen). Ekkor $e=\left(t+x_1\right)/4$ egész és $m=n/\left(t{x}_1\right)$. (Megoldást kapunk akkor is, ha $t$ és $x_1$ nem relatív prím, csak így egyes megoldásokat többször is megkaphatunk.)   II. megoldás. A feladatnak csak azt a részét bizonyítjuk, hogy ha az (1) egyenlet megoldható, akkor van $n$-nek $4k-1$ alakú prímosztója. A törteket eltávolítva és 0-ra redukálva a $\begin{array}{c}{\displaystyle 4xy-n\left(x+y\right)=0}\end{array}$ összefüggést kapjuk. Szorozzunk 4-gyel és adjunk mindkét oldalhoz $n^2$-et, ekkor a bal oldal szorzattá alakítható. $\begin{array}{c}{\displaystyle \left(4x-n\right)\left(4y-n\right)=n^2\mathrm{.}}\end{array}$ Itt a bal oldali tényezők pozitívok, mert (1)-ből $1/x$ is, $1/y$ is kisebb $4/n$-nél, s így $\begin{array}{c}{\displaystyle 4x>n\mathrm{,}4y>n\mathrm{.}}\end{array}$ Ha $n$-nek nincs $4k-1$ alakú prímosztója, akkor nem állhat fenn az egyenlet, ekkor ugyanis $4x-n$ is, $4y-n$ is $4k-1$ alakú, tehát mint az előző megoldásban láttuk, van $4k-1$ alakú prímosztójuk. Ekkor azonban a bal oldalt prímtényezőkre bontva, azok közt lennének $4k-1$ alakú prímek, a jobb oldalon viszont beírva $n$ prímtényezős felbontását, csupa $4k+1$ alakú prímszám szorzata állna, ez pedig ellentmond annak, hogy minden 1-nél nagyobb természetes szám a tényezők sorrendjétől eltekintve egyértelműen írható fel prímtényezők szorzataként.   Megjegyzés. Lényeges volt, hogy a természetes számok körére szorítkozunk, s ezért meg kellett állapítani, hogy a szorzat tényezői pozitívok. Ezt a legtöbb versenyző, aki ezt az utat választotta, elmulasztotta. Pedig írhatjuk az egyenlőséget $\begin{array}{c}{\displaystyle \left(n-4x\right)\left(n-4y\right)=n^2}\end{array}$ alakban is, és ekkor semmi probléma nem látszik adódni abból, ha $n$ minden prímosztója $4k+1$ alakú. Valóban van is megoldása az (1) egyenletnek, ha csak azt kívánjuk, hogy $x$ és $y$ egész legyen és $n=4k+1$: $\begin{array}{c}{\displaystyle \frac{4}{n}=\frac{4k}{kn}=\frac{n-1}{kn}=\frac{1}{k}-\frac{1}{k\cdot n}=\frac{1}{k}+\frac{1}{-kn}\mathrm{.}}\end{array}$ 3. feladat. Adott teniszversenyzők két csoportja: az egyik $1000$, a másik $1001$ versenyzőből áll. Mindegyik csoporton belül ismerjük a versenyzők erősorrendjét. Adjunk meg olyan eljárást, amelynek segítségével $11$ mérkőzés lejátszása után megállapítható, ki a $2001$ játékos közül a középső (tehát az $1001$-edik). (Feltesszük, hogy a játékosok mind különböző erősségűek, és az erősebb játékos mindig legyőzi a gyengébbet.)   A teniszezők csoportjait nagybetűkkel fogjuk jelölni, az egyes versenyzőket a megfelelő kisbetűvel, indexként melléírva, hogy a legerősebbtől kezdve hányadik erősségben a saját csoportján belül.   I. megoldás. A játszmákat úgy kell választanunk, hogy eredményük alapján minél erősebben szűkíthessük azoknak a körét, akik közt az összesített sorrendben 1001-edik teniszező lehet. Ha egy $A$ és egy $B$ csoport összesített sorrendjében a $k$-adik versenyzőt keressük, akkor egy később alkalmasan választandó $i$ értékkel $a_i$-t és $b_{k-i}$-t küldjük pályára. Ekkor a győztesnél csak azok lehetnek jobbak, akik $a_i$-nél is, $b_{k-i}$-nél is jobbak (8. ábra), a vesztesnél pedig még a győztes is, tehát eggyel több teniszező. 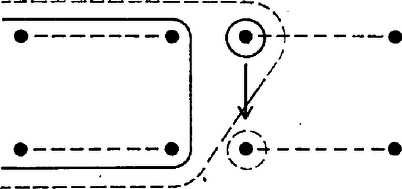  8. ábra   A győztesnél tehát legfeljebb $\left(i-1\right)+\left(k-i-1\right)=k-2$ erősebb versenyző lehet. Így ő a $\left(k-1\right)$-edik vagy annál erősebb az összesített sorrendben. A $k$-adik helyre tehát nem jön szóba, a nála erősebbek természetesen szintén nem. A vesztesnél legalább eggyel több versenyző erősebb, tehát legalább $k-1$. Így ő még esetleg lehet $k$-adik, de a nála gyengébbek már nem. A 9. ábrán a nyíl a győztestől mutat a vesztesre. A zárójelbe tett versenyzők nem lehetnek már $k$-adika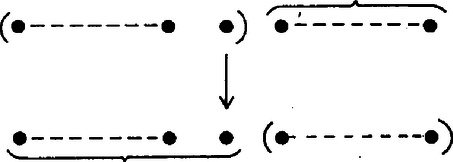k.   9. ábra   Ha az $A$ csapatban $2n+1$ versenyző van, a $B$-ben $2n$, tehát az összsorrendben $2n+1$-edik versenyzőt keressük. Válasszuk $i$-t $n+1$-nek, tehát küzdjön meg $a_{n+1}$ és $b_n$. Ha $a_{n+1}$ az erősebb, akkor a $2n+1$-edik versenyző $a_{n+2}$, $\text{...}$, $a_{2n+1}$ és $b_1$, $\text{...}$, $b_n$ közül kerül ki, és ezeket állítva sorrendbe, köztük őt az $n$-edik helyen találjuk, hiszen $a_1$, $\text{...}$, $a_{n+1}$-et azért hagyhatjuk figyelmen kívül, mert biztosan erősebbek a $2n+1$-edik versenyzőnél. Ha viszont $b_n$ erősebb $a_{n+1}$-nél, akkor a középső versenyző $a_1$, $\text{...}$, $a_{n+1}$ és $b_{n+1}$, $\text{...}$, $b_{2n}$ közül kerül ki, tehát egy $n+1$ és egy $n$ fős csoport teniszezői közül, és köztük ő az $n+1$-edik, azaz középső, hiszen $n$ olyan teniszezőt hagytunk figyelmen kívül, akik biztosan erősebbek nála. Az első esetben 2 versenyző tekinthető középsőnek, közülük az erősebbet kell keresnünk. Ha $A$-ban $2n$ versenyző van, $B$-ben $2n-1$, és az összesített sorrendben a $2n$-ediket keressük, akkor $a_n$ és $b_n$ mérje össze erejét. Aszerint, hogy $a_n$ vagy $b_n$ győz-e, $a_{n+1}$, $\text{...}$, $a_{2n}$ és $b_1$, $\text{...}$, $b_n$ közül, vagy pedig $a_1$, $\text{...}$, $a_n$ és $b_{n+1}$, $\text{...}$, $b_{2n-1}$ közül kell keresnünk az $n$-ediket, tehát két $n$ tagú csoportból az erősebb középsőt, vagy egy $n$ és egy $n-1$ tagú csoportból a középsőt. Meg kell vizsgálnunk két egyenlő létszámú csoport esetét is, mert láttuk, ilyenre is vezethet eljárásunk. Ilyen esetekben idáig a két középen levő versenyző közül az erősebbet kellett keresni. Ha $A$ is, $B$ is $2n$ tagú és a $2n$-edik versenyzőt keressük, akkor $a_n$ és $b_n$ csapjon össze. Az $A$ és $B$ csoport szerepe most teljesen szimmetrikus, elég tehát azt az esetet vizsgálni, ha $a_n$ győz. Ekkor $a_{n+1}$, $\text{...}$, $a_{2n}$ és $b_1$, $\text{...}$, $b_n$ közül kell az $n$-ediket keresnünk, tehát két egyenlő csoport egyesített listáján az erősebbik középsőt. Ha végül $A$ is, $B$ is $2n+1$ versenyzőből áll, és az összesítésben $2n+1$-edik versenyzőt keressük, akkor kézenfekvő, hogy eddigi formulánktól kissé eltérve a két középsőt: $a_{n+1}$-et és $b_{n+1}$-et küldjük pályára. Ismét elég azt az esetet vizsgálni, ha $a_{n+1}$ győz (10. ábra). 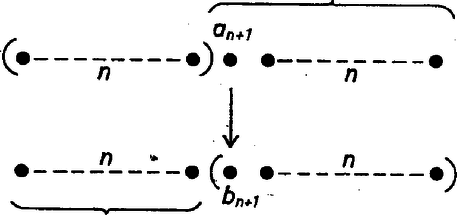  10. ábra   Ekkor $n$ csoporttársa gyengébb nála, $B$-ből pedig legalább $n+1$-en, tehát az erőlistán $2_{n+1}$-edik még lehet, de az őt megelőző csoporttársai már megelőzik a $2n+1$-edik versenyzőt. $b_{n+1}$-nél $n$ csoporttársa erősebb és $A$-ból legalább $n+1$ teniszező, tehát ő legalább $2n+2$-edik, a nála gyengébb csoporttársai pedig még hátrább vannak. Így $a_{n+1}$, $\text{...}$, $a_{2n+1}$ és $b_1$, $\text{...}$, $b_n$ közül kell még kiválasztani az $n+1$-ediket, vagyis egy $n+1$-es és egy $n$-es csoportból ismét a középsőt. Minden esetben azt kaptuk tehát, hogy a versenyzők összlétszáma egy‐egy lépésben megfeleződik, vagy ha páratlan volt, a rosszabbik esetben féllel több lesz a felénél. Eszerint 2001 versenyző esetén eljárásunk mellett az egyes játszmák eredménye a legrosszabb esetben a következőképpen alakulhat:     Legkésőbb a 11-edik lépés után tehát kiderül, ki a középső. Ezzel igazoltuk a feladat állítását.   Megjegyzések. 1. Minden lépés után felírva a két csoport lehetséges alakulását, a következő táblázatot kapjuk: Eszerint eljárásunk a legszerencsésebb esetben is csak 10 lépésben vezet célhoz. 2. A 11-es szám optimális abban az értelemben, hogy nem lehetséges olyan algoritmus, amelyik 10 lépésben megtalálja a középső versenyzőt, bárki legyen is az. Ez azért van így, mert van 2001 versenyző, akik közül bárki lehet a középső. Másrészt viszont csak egy $a$ és egy $b$-beli játékost van értelme játszatni egymással, mert egy csoportbelieknél tudjuk már a játszmák kimenetelét. Egy‐egy játszmában vagy az $A$-beli vagy a $B$-beli játékos győz, tehát kétféle kimenetel lehetséges. A 10 játszmának együtt eszerint $2^{10}=1024$ különböző kimenetele lehet. Semmilyen algoritmus esetén sem kaphatunk 10 mérkőzésből 2001 különböző választ. 3. Váratlannak látszik, hogy a két páratlan csoport esetében változtatni kellett a stratégián. Akkor lesz $a_i$, a $k$-adik, ha $b_{k-i}$-től (ha $k>i$) kikap, de $b_{k-i+1}$-et (ha $B$-ben van legalább $k-i+1$ játékos) már megveri. A fenti eljárásban a két itt említett játszmából mindig az előbbi típusút játszattuk le, a mondott esetben azonban az utóbbi típusú volt a célszerű. Érdekes megjegyezni, hogy a két típusú játszma minden esetben egymásba megy át, ha ahelyett, hogy a legerősebbtől kiindulva rangsorolnánk a versenyzőket, a leggyengébbtől sorszámoznánk, és "gyengébb''-et és "erősebb''-et mindenütt felcserélnénk, kivéve egyedül azt az esetet, amikor két egyenlő páratlan létszámú csoportnál keressük a középsők közül akár az erősebbet, akár a gyengébbet. 4. Sok versenyző a szimmetria kedvéért úgy hagyott el mindig versenyzőket, hogy páratlan számú versenyző maradjon vissza, és azok közül ismét a középsőt kelljen keresni. A leírt eljárástól tehát annyiban tért el, hogy amikor két különböző létszámú csoportból elég volt csak két egyenlő létszámú részt megtartani, akkor még az éppen lejátszott mérkőzés győztesét is visszatartotta. Ilyen módon $2n+1$ és $2n$ versenyzőből mindig $n+1$ és $n$ marad vissza, $2n$ és $2n-1$-ből viszont a kedvezőtlenebb esetben két $n$-es csoport helyett szintén $n+1$ és $n$, összlétszámban tehát $4n-1$-ből is, $4n+1$-ből is $2n+1$. Az egyes mérkőzések után eszerint így alakulna az összlétszám:     Itt egy 1-es és egy 2-es csoport maradt. Ha az egyedül levő győz az erősebb partner ellen, akkor a vesztes a középső, de ha nyer, akkor még a gyöngébbel is meg kell mérkőznie. (A győztes bennhagyása összesen 3 játékos esetén nem vezetne csökkenéshez, így el kell térni az általános előírástól.) Az ötödik lépésben nem lépünk át 2 egy hatványán, és emiatt lehet szükség egy 12-ik játszmára is. Itt 1 tényleges versenyző fölösleges bennhagyása már elrontotta az algoritmust, viszont ha ügyesebben csináljuk, sok "kitalált'' játékost is hozzávehetünk a meglevőkhöz, és ezzel nem rontjuk, csak egyszerűsítjük a helyzetet. Erre a gondolatra többen is rájöttek, de igazán jól csak Tardos Gábor használta ki.   II. megoldás. Helyezzünk az 1001-es $A$ csoport elejére 23 képzelt játékost, akikről tudjuk, hogy minden valódi játékosnál erősebb matadorok, és egymás közti sorrendjük is ismert, az 1000-es $B$-csoport végére pedig 24 dilettánst, aki minden valódi játékosnál és a 23 matadornál gyengébb, és egymás közti sorrendjük is adott. (A kitalált emberek esetleges játszmáit tehát nem kell ténylegesen lejátszani, azok kimenetelét előre tudjuk.) A 23 matadort is beleszámítva, ebben a helyzetben az összesített sorrend 1024-edik emberét kell megkeresnünk. Vizsgáljuk általánosan azt a kérdést, hogy két $2^L$ létszámú csapatból, amelyekben külön‐külön ismerjük az erőviszonyokat, hogyan választhatjuk ki, hogy ki van az összesített lista $2^L$-edik helyén. Kényelmesebb lesz most a leggyengébbtől kezdve sorszámozni rangsorban az egyes csapatok tagjait, a leggyengébbnek adva az 1-es számot. Olyan helyzeteket fogunk létrehozni, amelyekben valamilyen $n$-re $a_n$ jobb, mint $b_{2^L-n}$ és $a_{n-2^k}$ gyengébb, mint $b_{2^L-n+2^k}$. ($L\ge k\ge 0$). Egy ilyen helyzetben mérkőzzék meg $a_{n-2^{k-1}}$ és $b_{2^L-n+2^{k-1}}$. Ha az előbbi nyer, akkor legyen $n\text{'}=n-2^{k-1}$, ha az utóbbi, akkor $n\text{'}=n$. Ekkor világos, hogy a kiindulási helyzetet kaptuk vissza $n$ és $k$ helyett $n\text{'}$-vel és $k-1$-gyel.   11. ábra   A kezdeti helyzetet is felfoghatjuk ilyennek, ha csapatunk legelejére odaképzelünk egy $a_0$, ill. $b_0$ versenyzőt, akik minden eddigi teniszezőnél rosszabbak. Ekkor $n=k=2^L$-lel fennáll, hogy $a_{2^L}$ erősebb $b_0=b_{2^L-2^L}$-nél és $a_{2^L-2^L}=a_0$ gyengébb $b_{2^L-2^L+2^L}=b_{2^L}$-nél. (Ehhez nincs szükség tényleges játékra.) Ebből a helyzetből kiindulva az $L$-edik lépés után ott fogunk tartani, hogy valamilyen $n$-re $a_n$ jobb, mint $b_{2^L-n}$ és $a_{n-1}$ gyengébb, mint $b_{2^L-n+1}$, (11. ábra). Ekkor utolsó mérkőzésre álljon ki a két győztes: $a_n$ és $b_{2^L-n+1}$. Mindketten erősebbek $A$-ból $n-1$ játékosnál, $B$-ből $2^L-n$-nél, összesen $2^L-1$-nél. A vesztes az összes többinél gyengébb, így ő a keresett játékos. A kérdés eldöntéséhez $L+1$ játszma elég volt. Esetünkben a (kipótolt) csapatok létszáma $1024=2^{10}$, így 11 lépésben vezet célra eljárásunk. (Vagy kevesebb lépésben, ha közben képzelt emberek játszmájára is sor kerül.)   Megjegyzés. Beláthatjuk, hogy a tárgyalt speciális esetek: egyenlő vagy majdnem egyenlő két csoportból a középső megkeresése, csak látszólag speciális, az általános visszavezethető erre. Legyen az $A$ csoport $m$ tagú, a $B$ csoport $n$-tagú és keressük a versenyzők összesített rangsorában a $k$-adik versenyzőt ($1\le k\le m+n$). Legyen az elejéről $k$-adik versenyző a rangsor végétől számított $k\text{'}$-edik, ekkor $k+k\text{'}=m+n+1$, (12. ábra) tehát a kisebbikük ‐ vagy a közös értékük, ha egyenlők ‐ nem nagyobb, mint $\left(m+n+1\right)/2$. Feltehetjük, hogy $k$ nem nagyobb ennél az értéknél, mert ellenkező esetben csak a "gyengébb'', "erősebb'', valamint a "győz'', "veszít'' szavakat (és szinonímáikat) kell felcserélni, és ezzel $k$ és $k\text{'}$ is szerepet cserél.     12. ábra   Ha $k\le m\le n$, akkor csak $a_1$, $\text{...}$, $a_k$ és $b_1$, $\text{...}$, $b_k$ jön tekintetbe a $k$-adik helyre, és így két $k$ fős csapatból kell kiválasztani azt, aki az összesített sorrendben a két középső közül az erősebb. Ha viszont $m<k\le \left(m+n+1\right)/2$, akkor $\begin{array}{c}{\displaystyle n-k\ge n-\frac{m+n+1}{2}=\frac{n-m+1}{2}>\mathrm{0,}}\end{array}$ tehát $k<n$. Ekkor $k<j\le n$-re $b_j$ nem lehet $k$-adik, de nem lehet $b_1$, $\text{...}$, $b_{k-m-1}$ sem, mert még ha az $A$ csoport mind az $m$ tagja erősebb is náluk, akkor sincs egyikük sem a $k-1$-edik helynél hátrább. A $B$ csoportból tehát csak $\begin{array}{c}{\displaystyle n-\left(k-m-1\right)-\left(n-k\right)=m+1}\end{array}$ játékost kell figyelembe venni és közülük a ranglista $\begin{array}{c}{\displaystyle k-\left(k-m-1\right)=m+1}\end{array}$ sorszámú tagját keresni, mert a $k$-adik versenyzőnél biztosan jobb $k-m-1$ versenyzőt figyelmen kívül hagyhattunk. Ez esetben tehát egy $m$ és egy $m+1$ létszámú csapatból kell a rangsorban középsőt kikeresni. A szükséges játszmák számára a II. megoldás eljárása azt adja, hogy ha két egyenlő vagy 1-gyel különböző létszámú csapatból kell az összesített ranglistán középső, ill. a középsők közül (mondjuk) erősebb versenyzőt kiválasztani, akkor ezt $L$ lépésben megtehetjük, ahol $L$ azzal van meghatározva ‐ ha a versenyzők összlétszámát $N$-nel jelöljük ‐, hogy $\begin{array}{c}{\displaystyle 2^{L-1}<N\le 2^L\mathrm{.}}\end{array}$ Az I. megoldáshoz fűzött 2. jegyzet gondolatmenetével látható, hogy ennél kevesebb lépés nem lehet minden esetben elegendő.${}^{*}$ Surányi János ${}^{*}$A feladatok szövegének idegennyelvű fordításait következő számunkban közöljük.