Kezdőlap


Cím:	A finnországi Nemzetközi Matematikai Verseny feladatainak megoldása- 1980.
Szerző(k):	Reiman István
Füzet:	1981/január, 1 - 8. oldal	PDF \| MathML
Témakör(ök):	Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Jelöljük egy tetszőleges $A B C$ háromszög szögeit rendre $α$ -val, $β$ -val, illetve $γ$ -val. Az $A B$ oldal felező merőlegese messe a $B C$ oldalt vagy annak meghosszabbítását az $X$ pontban, az $A C$ oldal felező merőlegese pedig ugyanezt az $Y$ pontban. Bizonyítsuk be, hogy $B C = X Y$ teljesülésének elegendő feltétele: $tg β \cdot tg γ = 3$ . Mutassuk meg, hogy ez a feltétel nem szükséges, és adjuk meg $B C = X Y$ teljesülésének elegendő feltételét.

Megoldás. Helyezzük el az

A B C

háromszöget a koordináta-rendszerben úgy, hogy a csúcsok koordinátái

A (a_{1}; a_{2})

B (- 1; 0)

C (1; 0)

legyenek. Az a célunk, hogy az

X Y

szakasz hosszát

tg β \cdot tg γ

segítségével fejezzük ki.
Mivel az

A B

egyenes iránytangense,

tg β = a_{2} / (1 + a_{1})

és az

A C

egyenesé

tg (180^{\circ} - γ) = - tg γ = a_{2} / (a_{1} - 1)

és így

tg γ = a_{2} / (1 - a_{1})

azért

\begin{matrix} tg β \cdot tg γ = \frac{a_{2}^{2}}{1 - a_{1}^{2}} . \end{matrix}

(1)

A B

felező merőlegesének egyenlete:

(a_{1} + 1) x + a_{2} y = \frac{a_{1}^{2} + a_{2}^{2} - 1}{2}

, az

A C

felező merőlegeséé pedig: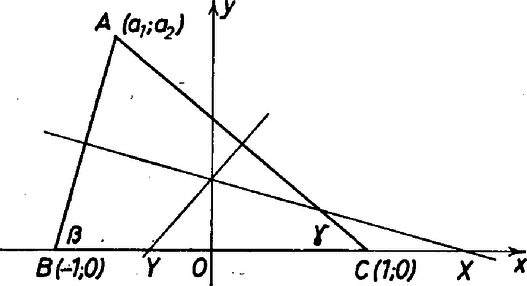

(a_{1} - 1) x + a_{2} y = \frac{a_{1}^{2} + a_{2}^{2} - 1}{2}

1. ábra

Ezekbe

y = 0

-t helyettesítve, majd rendezve megkapjuk a felező merőlegesek és az

x

tengely (azaz a

B C

egyenes) metszéspontjainak az abszcisszáit. A metszéspontok koordinátái:

\begin{matrix} X (\frac{a_{1}^{2} + a_{2}^{2} - 1}{2 (a_{1} + 1)}; \end{matrix}

Ebből az

X Y

szakasz hossza (figyelembe véve, hogy a két abszcissza különbsége negatív is lehet):

\begin{matrix} X Y = | \frac{a_{1}^{2} + a_{2}^{2} - 1}{2} (\frac{1}{a_{1} + 1} - \frac{1}{a_{1} - 1}) | = | \frac{a_{1}^{2} + a_{2}^{2} - 1}{1 - a_{1}^{2}} | = | - 1 + \frac{a_{2}^{2}}{1 - a_{1}^{2}} | . \end{matrix}

Az (1) alatti érték helyettesítésével,

\begin{matrix} X Y = | - 1 + tg β \cdot tg γ | . \end{matrix}

Mivel a koordináta-rendszer választása miatt

B C = 2

, az

X Y = B C

, akkor és csakis akkor teljesül, ha

- 1 + tg β \cdot tg γ = \pm 2

, azaz vagy

tg β \cdot tg γ = 3

, vagy pedig

tg β \cdot tg γ = - 1

; a megoldás menete éppen azt mutatja, hogy mindkét kapott feltétel elégséges

X Y = B C

teljesüléséhez és a kettő közül az egyik teljesülése szükséges is.

Megjegyzés. A sokféle megoldási lehetőség közül az analitikus geometriait azért részesítettük előnyben, mert az egyszerre szolgáltatta a szükséges és elégséges feltételt. Simonyi Gábor megoldásának első fele azon az észrevételen alapult, hogy

tg β \cdot tg γ = 3

teljesülése esetén a háromszög magasságpontját, súlypontját és a köré írt kör középpontját felfűző Euler-féle egyenes párhuzamos a

B C

oldallal. Mint érdekességet említjük meg, hogy ennek a tételnek egy szép bizonyítását közölte a Középiskolai Mathematikai Lapok

1902

-ben, Haar Alfrédnak, a világhírű matematikusnak a tollából.

2. Az

a_{0}, a_{1}, ..., a_{n}

számokat a következőképpen definiáltuk

(n > 1)

\begin{matrix} a_{0} = \frac{1}{2}, a_{k + 1} = a_{k} + \frac{a_{k}^{2}}{n}, h a k = 0, 1, ..., n - 1. \end{matrix}

Bizonyítsuk be, hogy

1 - \frac{1}{n} < a_{n} < 1

Megoldás. A számok definíciójából következik, hogy

\begin{matrix} a_{0} < a_{1} < a_{2} < ... < a_{n} . \end{matrix}

(2)

A bizonyítás céljára az

\frac{1}{a_{k}} - \frac{1}{a_{k + 1}}

különbség vizsgálata bizonyul célravezetőnek:

\begin{matrix} \frac{1}{a_{k}} - \frac{1}{a_{k + 1}} = \frac{a_{k + 1} - a_{k}}{a_{k} a_{k + 1}} = \frac{a_{k}^{2}}{n a_{k} (a_{k} + \frac{a_{k}^{2}}{n})} = \frac{1}{n + a_{k}} k = 0, 1, ..., n - 1. \end{matrix}

(2) alapján ebből már következik, hogy

\begin{matrix} \frac{1}{n + a_{n}} < \frac{1}{a_{k}} - \frac{1}{a_{k + 1}} < \frac{1}{n} . \end{matrix}

Összegezzük most az ilyen típusú egyenlőtlenségeket

k = 0

-tól

(n - 1)

-ig:

\begin{matrix} \frac{n}{n + a_{n}} < \sum_{k = 0}^{n - 1} (\frac{1}{a_{k}} - \frac{1}{a_{k + 1}}) < 1, \end{matrix}

azaz

\begin{matrix} \frac{n}{n + a_{n}} < \frac{1}{a_{0}} - \frac{1}{a_{n}} = 2 - \frac{1}{a_{n}} < 1. \end{matrix}

(3)

2 - \frac{1}{a_{n}} < 1

egyenértékű a bizonyítandó

a_{n} < 1

egyenlőtlenség-részlettel. Azt kell még igazolnunk, hogy

a_{n} > 1 - \frac{1}{n} = \frac{n - 1}{n}

, azaz

\begin{matrix} \frac{1}{a_{n}} < \frac{n}{n - 1} = 1 + \frac{1}{n - 1} . \end{matrix}

(4)

(3)-ból közvetlenül következik, hogy

\begin{matrix} \frac{1}{a_{n}} < 2 - \frac{n}{n + a_{n}} . \end{matrix}

Ha ehhez most még figyelembe vesszük a már bizonyított

a_{n} < 1

egyenlőtlenséget, kapjuk, hogy

\begin{matrix} \frac{1}{a_{n}} < 2 - \frac{n}{n + a_{n}} < 2 - \frac{n}{n + 1} = 1 + \frac{1}{n + 1} < 1 + \frac{1}{n - 1} \end{matrix}

és éppen ezt kellett igazolnunk.

3. Bizonyítsuk be, hogy az

\begin{matrix} x^{n} + 1 = y^{n + 1} \end{matrix}

egyenletnek, ahol

n

Megoldás. Írjuk fel egyenletünket

\begin{matrix} x^{n} = y^{n + 1} - 1 = (y - 1) (y^{n} + y^{n - 1} + ... + y + 1) \end{matrix}

(5)

alakban és tegyük fel, hogy van olyan

x

és

y

egész, amelyekre

x

és

n + 1

relatív prímek, de

x

és

y

kielégítik az egyenletet. Először megmutatjuk, hogy ebben az esetben

y - 1

és

y^{n} + y^{n - 1} + ... + y + 1

relatív prímek. Ha ui. lenne közös

p

törzstényezőjük, akkor valamilyen

A

és

B

egésszel

\begin{matrix} y - 1 = A p, y = A p + 1; & (6) \\ y^{n} + y^{n - 1} + ... + y + 1 = B p & (7) \end{matrix}

teljesülne. Végezzük el (7) jobb oldalán az

y = A p + 1

helyettesítést. Mivel

A p + 1

minden hatványában a binomiális tétel értelmében az

1

-en kívül

p

-vel osztható tagok szerepelnek, a helyettesítés eredményeként azt kapjuk, hogy valamely

C

egész számmal

\begin{matrix} C p + (n + 1) = B p, \end{matrix}

amiből viszont

(B - C) p = n + 1

adódik, de ez azt jelenti, hogy

p

osztója

n + 1

-nek, és (5) és (6) miatt

x

-nek is. Ellentmondásra jutottunk, mert így

n + 1

és

x

nem relatív prímek. Csak az lehetséges tehát, hogy

y - 1

és

y^{n} + y^{n - 1} + ... + y + 1

relatív prímek; viszont szorzatuk egy egész szám

n

-edik hatványa, ezért kell, hogy mindkét tényező teljes

n

-edik hatvány legyen. Azonban az

y^{n} < y^{n} + y^{n - 1} + ... + y + 1 < {(y + 1)}^{n}

miatt a második tényező két szomszédos egész

n

-edik hatványa közé esik, ezért nem lehet

n

-edik hatvány, ennélfogva ellentmondásra jutottunk, ami a feladat állítását bizonyítja.

4. Mely

n

természetes számokra érvényes a következő állítás: a körbe írható

A_{1} A_{2} ... A_{2 n - 1} A_{2 n}

konvex sokszögnél az

A_{1} A_{2}

;

A_{n + 1} + A_{n + 2}

A_{2} A_{3}

;

A_{n + 2} A_{n + 3}

...

A_{n - 1} A_{n}

;

A_{2 n - 1} A_{2 n}

szemközti oldalpárok párhuzamosságából következik az

A_{n} A_{n + 1}

A_{2 n} A_{1}

oldalpár párhuzamossága ?

Megoldás. Két megjegyzést bocsátunk előre. Az első: ha

A_{1}

A_{2}

A_{3}

és

B_{1}

B_{2}

B_{3}

egy kör olyan egymás utáni pontjai, hogy a két ponthármas körüljárási iránya azonos és

A_{1} A_{2} ∥ B_{1} B_{2}

és

A_{2} A_{3} ∥ B_{2} B_{3}

, akkor az

A_{2}

-t tartalmazó

A_{1} A_{3}

ív egyenlő a

B_{2}

-t tartalmazó

B_{1} B_{3}

ívvel (2. ábra).

2. ábra

Ez abból következik, hogy az

A_{1} A_{2} A_{3} ∢ = B_{1} B_{2} B_{3} ∢

, mert váltószögek, így az

A_{1} A_{3}

és

B_{1} B_{3}

ívekhez egyenlő kerületi szögek tartoznak, tehát egyenlők.
A második: ha az

A B

és

C D

ívek egy kör egyirányú, egyenlő hosszú ívei, akkor az

A D

és

B C

húrok párhuzamosak (3. ábra). A feltételből ui. következik, hogy

A C B ∢ = C A D ∢

(egyenlő ívekhez tartozó kerületi szögek), ezért a váltószögek tételének megfordításából következik, hogy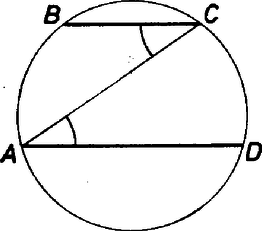

A D ∥ B C

3. ábra

Most megmutatjuk, hogy a feladat állítása páratlan

n

-ekre igaz. Tegyük fel ‐ a feladat kikötéseinek megfelelően ‐, hogy a körbe írt konvex

2 n

-szögben

A_{1} A_{2} ∥ A_{n + 1} A_{n + 2}

A_{2} A_{3} ∥ A_{n + 2} A_{n + 3}, ..., A_{n - 1} A_{n} ∥ A_{2 n - 1} A_{2 n}

A sokszög konvex voltából következik, hogy az

A_{1} A_{2} A_{3}

és

A_{n + 1} A_{n + 2} A_{n + 3}

, az

A_{3} A_{4} A_{5}

és

A_{n + 3} A_{n + 4} A_{n + 5}

..., A_{n - 2} A_{n - 1} A_{n}

és

A_{2 n - 2} A_{2 n - 1} A_{2 n}

ponthármasok egyező körüljárásúak; és ezért első megjegyzésünk értelmében

\hat{A_{1} A_{3}} = \hat{A_{n + 1} A_{n + 3}}, \hat{A_{3} A_{5}} =

= \hat{A_{n + 3} A_{n + 5}}, ..., \hat{A_{n - 2} A_{n}} = \hat{A_{2 n - 2} A_{2 n}}

, és mivel

n

páratlan, ezért a fentiekben az

\hat{A_{1} A_{n}}

és

\hat{A_{n + 1} A_{2 n}}

minden részívét felsoroltuk. Tehát

\hat{A_{1} A_{n}} = \hat{A_{n + 1} A_{2 n}}

, ebből viszont második megjegyzésünk alapján következik, hogy az

A_{1} A_{2 n}

és

A_{n} A_{n + 1}

oldalak is párhuzamosak (4. ábra).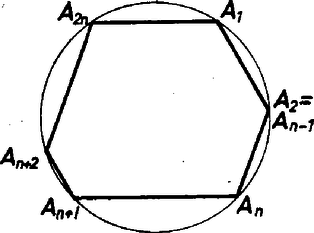

4. ábra

Egy ellenpéldán megmutatjuk, hogy ha

n

páros,

n - 1

oldalpár párhuzamosságából általában még nem következik az

n

-edik oldalpár párhuzamossága.
Válasszuk az egységsugarú körbe írt sokszög csúcsait úgy, hogy a szomszédos csúcsok közötti ívekre az alábbi feltételek teljesüljenek:

\begin{matrix} \hat{A_{1} A_{2}} = \hat{A_{3} A_{4}} = ... = \hat{A_{n - 1} A_{n}} = \frac{3 π}{2 n} = \hat{A_{n + 2} A_{n + 3}} = \hat{A_{n + 4} A_{n + 5}} = ... = \hat{A_{2 n - 2} A_{2 n - 1}}; \\ \hat{A_{2} A_{3}} = \hat{A_{4} A_{5}} = ... = \hat{A_{n - 2} A_{n - 1}} = \frac{π}{2 n} = \hat{A_{n + 1} A_{n + 2}} = \hat{A_{n + 3} A_{n + 4}} = ... = \hat{A_{2 n - 1} A_{2 n}}; \\ A_{n} A_{n + 1} = \frac{π}{n} = A_{2 n} A_{1} . \end{matrix}

Ez a felosztás szemléletesen azt jelenti, hogy háromféle körív fordul elő a szomszédos csúcsok között:

\frac{3 π}{2 n}

hosszúságú (I. típus), ennek harmadrésze,

\frac{π}{2 n}

hosszúságú (II. típus), és végül két ív hossza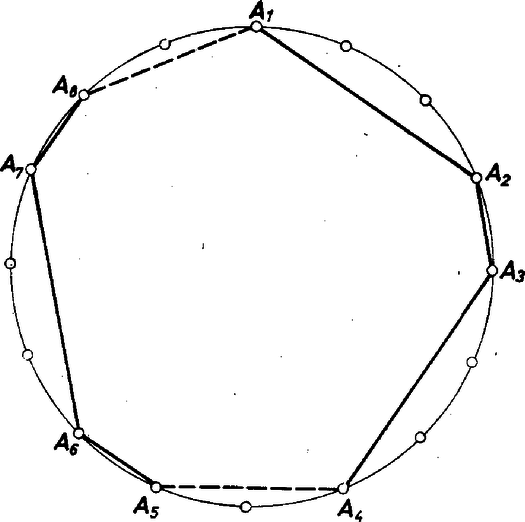

\frac{π}{n}

5. ábra

Az I-es és II-es típusú ívek felváltva követik egymást az

A_{1}

csúcstól az

A_{n}

-ig, majd újra az

A_{n + 1}

-ből

A_{2 n}

-ig (az 5. ábrán

n = 4

), a csúcsokat a körbe írt

4 n

oldalú szabályos sokszög csúcsaiból választjuk ki. Ebből következik, hogy ha kiválasztjuk az

A_{k} A_{k + 1}

és

A_{n + k} A_{n + k + 1}

oldalakat, ezek párhuzamosak lesznek, ha

k \neq n

, mivel az elrendezés miatt

\hat{A_{k + 1} A_{n + k}} = \hat{A_{n + k + 1} A_{k}}

, viszont

A_{n} A_{n + 1}

és

A_{2 n} A_{1}

nem lehetnek párhuzamosak, mert ehhez

\hat{A_{1} A_{n}} = \hat{A_{n + 1} A_{2 n}}

teljesülésére lenne szükség. Azonban

\hat{A_{1} A_{n}}

\frac{n}{2}

darab I. típusú és

\frac{n - 2}{2}

darab II. típusú ívből áll, tehát

\begin{matrix} \hat{A_{1} A_{n}} = \frac{n}{2} \cdot \frac{3 π}{2 n} + \frac{n - 2}{2} \cdot \frac{π}{2 n} = \frac{2 n - 1}{2 n} π; \end{matrix}

és

\hat{A_{n + 1} A_{2 n}}

\frac{n - 2}{2}

darab I. típusú és

\frac{n}{2}

darab II. típusú ívet tartalmaz, ezért

\begin{matrix} \hat{A_{n + 1} A_{2 n}} = \frac{n - 2}{2} \cdot \frac{3 π}{2 n} + \frac{n}{2} \frac{π}{2 n} = \frac{2 n - 3}{2 n} π, \end{matrix}

így tehát

A_{n} A_{n + 1}

valóban nem párhuzamos

A_{2 n} A_{1}

-gyel (Bohus Géza példája).

Megjegyzések. Komplex számok segítségével a feladat első részére egyszerű és általánosabb érvényű megoldást lehet adni, felhasználva azt, hogy ha a komplex számsík

0

pontja köré írt körön kiválasztjuk az

a

b

c

d

pontokat, az

a b

és

c d

húrok párhuzamosságának feltétele az

a b = c d

egyenlőség teljesülése. Jelöljük a sokszög csúcsaihoz tartozó komplex számokat a megfelelő kisbetűkkel (a sokszög középpontja a számsík

0

pontja). A feladat feltételei szerint

\begin{matrix} a_{1} a_{2} = a_{n + 1} a_{n + 2}, a_{n + 2} a_{n + 3} = a_{2} a_{3}, a_{3} a_{4} = a_{n + 3} a_{n + 4}, ..., a_{n - 1} a_{n - 2} = a_{2 n - 2} a_{2 n - 1}, \\ a_{2 n - 1} a_{2 n} = a_{n - 1} a_{n} \end{matrix}

Ezeknek az egyenlőségeknek megfelelő oldalait összeszorozva egyszerűsítés után az

a_{1} a_{2 n} = a_{n} a_{n + 1}

egyenlőséget kapjuk, ami éppen az

n

-edik oldalpár párhuzamosságát bizonyítja. Figyeljük meg, hogy ez a bizonyítás nem használta fel a sokszög konvex voltát, tehát az önmagát átmetsző sokszögvonalra is jó. Ilyen sokszöget mutat

n = 3

esetén a 6. ábra.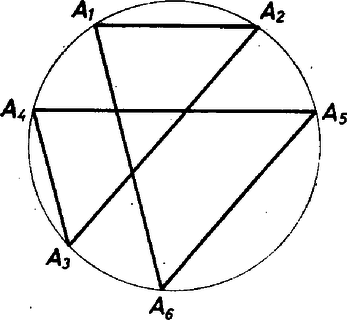

6. ábra

5. Valamely síkbeli derékszögű koordináta-rendszer

x

tengelyével párhuzamos egyenest akkor nevezünk triangulárisnak, ha balról jobbra haladva olyan különböző

A

B

C

és

D

pontokban metszi az

\begin{matrix} y = x^{4} + {p x}^{3} + {q x}^{2} + r x + s \end{matrix}

egyenletű görbét, hogy az

A B

A C

és

A D

szakaszok egy háromszög oldalai lehetnek. Bizonyítsuk be, hogy az

x

tengellyel párhuzamos egyenesek közül a szóban forgó görbét négy különböző pontban metszőknek vagy mindegyike trianguláris vagy egyik sem az.

Megoldás. A görbét egy, az

x

-tengellyel párhuzamos

e

egyenes messe rendre az

A

B

C

D

pontokban, legyenek az

A

koordinátái

A (t, d)

. Toljuk el a koordináta-rendszer kezdőpontját

A

-ba, a görbe egyenletét az új rendszerben az

x \to x + t, y \to y + d

helyettesítéssel kapjuk meg:

\begin{matrix} y + d = {(x + t)}^{4} + p {(x + t)}^{3} + q {(x + t)}^{2} + r (x + t) + s, \end{matrix}

ebből :

\begin{matrix} y = x^{4} + (4 t + p) x^{3} + (6 t^{2} + 3 p t + q) x^{2} + ({4 t}^{3} + {3 p t}^{2} + 2 t q + r) x + (t^{4} + p t^{3} + q t^{2} + r t + s) - d . \end{matrix}

Az új együtthatókat rendre

P

Q

R

S

-sel jelölve, a görbe egyenlete

\begin{matrix} y = x^{4} + {P x}^{3} + {Q x}^{2} + R x + S \end{matrix}

alakú, mivel azonban az origó rajta van a görbén,

S = 0

. Az

A

B

C

D

pontokhoz tartozó

x

értékek éppen az

\begin{matrix} x^{4} + {P x}^{3} + {Q x}^{2} + R x = 0 \end{matrix}

egyenlet gyökei, az

A

-hoz éppen az

x = 0

tartozik. A

B

C

D

pontok abszcisszáit jelölje rendre

t_{1}

t_{2}

t_{3}

(t_{1} < t_{2} < t_{3})

ezek tehát kielégítik az

\begin{matrix} x^{3} + {P x}^{2} + Q x + R = 0 \end{matrix}

egyenletet. Annak feltétele, hogy a

t_{1}

t_{2}

t_{3}

szakaszokból szerkeszthető legyen háromszög, az, hogy

- t_{1} + t_{2} + t_{3} > 0

t_{1} - t_{2} + t_{3} > 0

t_{1} + t_{2} - t_{3} > 0

egyenlőtlenségek teljesülnek (ebből az első kettő a nagyságrendi sorrend miatt eleve teljesül), azaz

\begin{matrix} (- t_{1} + t_{2} + t_{3}) (t_{1} - t_{2} + t_{3}) (t_{1} + t_{2} - t_{3}) > 0 \end{matrix}

(8)

kell, hogy fennálljon.
A harmadfokú egyenlet gyökei és együtthatói közötti összefüggés alapján

t_{1} + t_{2} + t_{3} = - P, t_{1} t_{2} + t_{2} t_{3} + t_{3} t_{1} = Q

; és

t_{1} t_{2} t_{3} = - R

. Mint arról számolással könnyen meggyőződhetünk, (8) bal oldalán

P^{3} - 4 P Q + 8 R

áll, tehát annak szükséges és elégséges feltétele, hogy az

e

egyenes trianguláris legyen az, hogy

\begin{matrix} δ = P^{3} - 4 P Q + 8 R > 0 \end{matrix}

teljesüljön. Viszont ‐ számolással ezt is könnyen igazolhatjuk ‐

\begin{matrix} δ = P^{3} - 4 P Q + 8 R = p^{3} - 4 p q + 8 r . \end{matrix}

tehát

δ

értéke független az

e

egyenes felvételétől, ezért ha egy

e

egyenesre

δ > 0

akkor mindre az; és ha egy egyenesre

δ \leq 0

, akkor mindegyikre ez teljesül, tehát a megengedett egyeneseknek vagy mindegyike trianguláris, vagy egyike sem az. (Hasonló elven alapuló bizonyítást adott a feladatra Tardos Gábor).

Megjegyzés. Egy egyszerű, de a szemléletnek nagyobb szerepet biztosító megoldást adott a feladatra Benkő Bálint. Ennek lényege: az

A

B

C

D

pontok trianguláris voltának a feltétele

A B < A C < A D

miatt

A D < A B + A C

, azaz

A B + B C + C D < A B + A B + B C

, tehát

C D < A B

, a négy pont egyenese viszont nem trianguláris, ha

C D \geq A B

. Tegyük most fel, hogy van egy

e

egyenes, amelyen

C D < A B

és egy másik

e'

egyenes, amelyen az

A'

B'

C'

D'

metszéspontokra a

C' D' \geq A' B'

teljesül. Az

e

egyenest

e'

felé tolva ezért van egy olyan

e^{*}

helyzet, amelyen az

A^{*}

B^{*}

C^{*}

D^{*}

metszéspontokra

C^{*} D^{*} = A^{*} B^{*}

áll 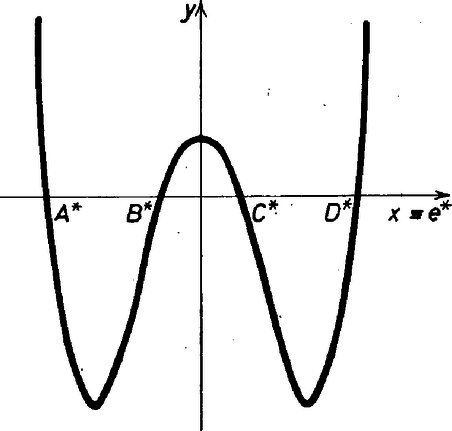fenn.

7. ábra

Ha viszont a koordináta-rendszert úgy választjuk, hogy az

x

tengely

e^{*}

-gal essék egybe, és

A^{*}

D^{*}

, ill.

B^{*}

C^{*}

szimmetrikusak legyenek az origóra (7. ábra), akkor a pontok abszcisszái rendre

a

- a

b

- b

alakúak, tehát a görbe egyenlete

\begin{matrix} y = (x + a) (x - a) (x + b) (x - b) = (x^{2} - a^{2}) (x^{2} - b^{2}) . \end{matrix}

Ez azt jelenti, hogy a görbe szimmetrikus az

y

tengelyre, tehát minden szóba jövő

e

egyenes esetén

A B = C D

, ami ellentmond annak a feltevésnek, hogy egyszerre létezik trianguláris és nem-trianguláris egyenes is.

6. Állapítsuk meg, hogy mely számjegyek állanak közvetlenül a tizedes vesszőtől balra és jobbra

\begin{matrix} {(\sqrt[]{2} + \sqrt[]{3})}^{1980} \end{matrix}

szám tízes számrendszerben felírt alakjában.

Megoldás. A vizsgálandó szám ,,nagyon kicsit'' változik, ha hozzáadjuk a reciprokát,

{(\sqrt[]{3} - \sqrt[]{2})}^{1980}

-t: Legyen

\begin{matrix} A = {(\sqrt[]{3} + \sqrt[]{2})}^{1980} + {(\sqrt[]{3} - \sqrt[]{2})}^{1980} . \end{matrix}

Mivel

\begin{matrix} {(\sqrt[]{3} + \sqrt[]{2})}^{2} = 5 + 2 \sqrt[]{6} és {(\sqrt[]{3} - \sqrt[]{2})}^{2} = 5 - 2 \sqrt[]{6}, \end{matrix}

azért

\begin{matrix} A = {(5 + 2 \sqrt[]{6})}^{990} + {(5 - 2 \sqrt[]{6})}^{900} . \end{matrix}

Fejtsük most ezt ki a binomiális tétel segítségével

\begin{matrix} A = 5^{990} + (\binom{990}{1}) 5^{989} \cdot 2 \sqrt[]{6} + ... + (\binom{990}{989}) 5 \cdot {(2 \sqrt[]{6})}^{989} + {(2 \sqrt[]{6})}^{990} + 5^{990} - \\ - (\binom{990}{1}) 5^{989} \cdot 2 \sqrt[]{6} + ... - (\binom{990}{989}) 5 \cdot {(2 \sqrt[]{6})}^{989} + {(2 \sqrt[]{6})}^{990} = 2 \cdot 5^{990} + ... + \\ + 2 (\binom{990}{988}) 5^{2} \cdot 2^{988} \cdot 6^{494} + 2 \cdot 2^{990} \cdot 6^{495} . \end{matrix}

A kapott összeg minden tagja egész, ezért

A

is egész, és az utolsó tag kivételével minden tag osztható

10

-zel, ezért

A

végződése az utolsó tag végződésével azonos. Az utolsó tag:

2^{991} \cdot 6^{495}

Tudjuk; hogy

6

minden hatványa

6

-ra végződik,

2

hatványainak a végződései pedig rendre

2, 4, 8, 6, ...

s innen periodikusan ismétlődik. Mivel

991 = 4 \cdot 247 + 3

, azért

2^{991}

8

-ra végződik és így

A

végződése

8 \cdot 6

végződésével azonos, tehát

8

-cal.
Viszont

5 - 2 \sqrt[]{6} < 0, 2

, ezért

{(5 - 2 \sqrt[]{6})}^{990} < {(0, 2^{2})}^{495} = 0, 04^{495} < 0, 1^{495}

, tehát

{(5 - 2 \sqrt[]{6})}^{990}

tízes számrendszerbeli alakjában a tizedesvessző után legalább

495

nulla következik, ezért

\begin{matrix} {(\sqrt[]{3} + \sqrt[]{2})}^{1980} = {(5 + 2 \sqrt[]{6})}^{990} = A - {(\sqrt[]{3} - \sqrt[]{2})}^{1980} = \\ = \bar{X X X ... 8} - \bar{0, 00 ... 0 X X ...} = \bar{X X X ... 7, 999 ... X X ...} \end{matrix}

a tizedesvessző mellett álló számjegyek tehát

... 7, 9 ...

Megjegyzés. Eredményre juthatunk az

\begin{matrix} U_{n} = {(5 + 2 \sqrt[]{6})}^{n} + {(5 - 2 \sqrt[]{6})}^{n} \end{matrix}

sorozat vizsgálatával is. Megmutatható, hogy a sorozatelemek kielégítik az

U_{n + 2} =

= 10 U_{n + 1} - U_{n}

ún. rekurziós formulát, azaz

U_{n} + U_{n + 2} = 10 U_{n + 1}

, azaz a sorozat másodszomszédos elemeinek az összege

10

-zel osztható; mivel

U_{1} = 10

U_{2} = 98

, ezért a sorozatelemek végződései:

0

8

0

2

0

8

0

2 ...

és emiatt

U_{990}

8

-ra végződik.