Cím:	Csillagötszögek
Füzet:	1981/április, 172 - 173. oldal	PDF  |  MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Csillagötszögek 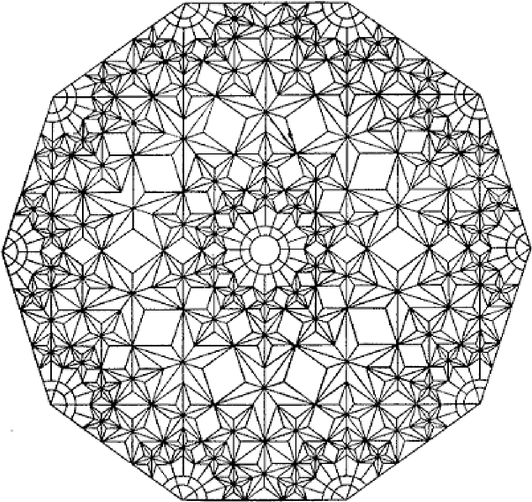  Hátsó borítónkon egy szabályos tízszögbe különböző méretű szabályos csillagötszögeket rajzoltunk. Ha az ötszögek rajzolását a megadott minta alapján vég nélkül folytatjuk, akkor végül a tízszög területének hányad részét fedjük le? Erre a kérdésre válaszolunk. Vegyük észre, hogy a legnagyobb csillagötszögből éppen 10 darab van,; az eggyel kisebb méretűből 40; a még eggyel kisebb méretűből (az ábrán szereplő legkisebb csillagötszögből) pedig 50. Ha a következő sorozat ötszöget rajzoljuk be, akkor a középpont körül 10, a sarkoknál 4‐4 új ötszög kerül a tízszögbe, azaz ismét 50. Így ha az $i$-edik méretű ötszög területe $t_i$, akkor a csillagok által lefedett terület 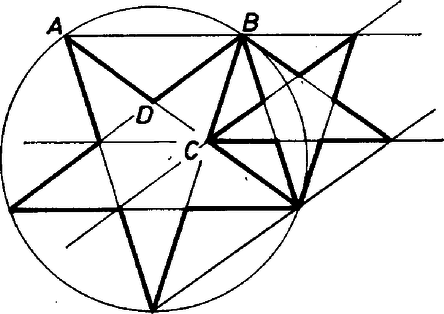$\begin{array}{c}{\displaystyle T=10t_1+40t_2+50t_3+50t_4+\text{...}+50t_n+\text{...}\mathrm{.}}\end{array}$ Vegyük észre még azt is, hogy ezek a csillagok mind hasonlóak egymáshoz, és hasonlóságuk aránya az 1. ábra szerint $\begin{array}{c}{\displaystyle q=BC:AB\mathrm{.}}\end{array}$   1. ábra   Ezt az arányt könnyen ki tudjuk számítani. Mivel $A$ és $B$ egy szabályos ötszög két egymás utáni csúcsa, azért $BAC\sphericalangle ={36}^{\circ }$, valamint $ABC\sphericalangle ={72}^{\circ }$, és így az $ABC$ háromszög egyenlő szárú. Hasonlóan az $ABD$ és a $BCD$ háromszög is egyenlő szárú, és ez utóbbi hasonló az $ABC$ háromszöghöz. De $CD=AC-AD=AB-BD=AB-BC$, és így az $AB:BC=BC:CD$ aránypárból $\begin{array}{c}{\displaystyle B{C}^2=AB\cdot CD=AB\cdot \left(AB-BC\right)=A{B}^2-AB\cdot BC\mathrm{,}}\end{array}$ azaz $\begin{array}{c}{\displaystyle q^2={\left(\frac{BC}{AB}\right)}^2=1-\frac{BC}{AB}=1-q\mathrm{,}}\end{array}$ ahonnan $q>0$ alapján $q=\left(\sqrt[]{5}-1\right)/2$. Hasonló alakzatok területének aránya a hasonlósági arányuk négyzetével egyenlő. Tehát $q^2=t_1:t_2=t_2:t_3=\text{...}$, amiből $T$ értéke $\begin{array}{c}{\displaystyle T=t_1\left(10+40q^2+50q^4\text{...}+50q^{2n}+\text{...}\right)\mathrm{.}}\end{array}$ Használjuk fel, hogy $0<q^2<1$, és ekkor az $1+q^2+q^4+\text{...}$ végtelen mértani sor határértéke (összege) éppen $1/\left(1-q^2\right)$, s azt kapjuk, hogy $\begin{array}{c}{\displaystyle T=30t_1\left(\sqrt[]{5}-1\right)\mathrm{.}}\end{array}$ Már csak $t_1$ értékét kell meghatároznunk. A 2. ábrán felrajzoltuk az egyik legnagyobb csillagötszöget és a szabályos tízszögnek a hozzá tartozó középponti háromszögét. 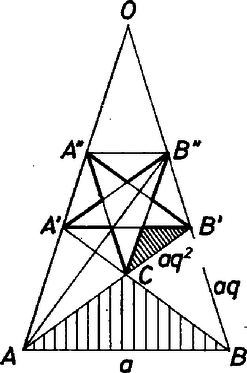  2. ábra   Csak úgy, mint az előbb, most is azt kapjuk, hogy $AB:BB\text{'}=BB\text{'}:B\text{'}C=q$. Tegyük fel, hogy az $OAB$ háromszög területe éppen $1$, azaz a szabályos tízszög területe $10$. Ekkor az $ABB\text{'}$ háromszög területe $q^2$, hiszen az $OAB$ és az $ABB\text{'}$ háromszögek hasonlóak, és hasonlósági arányuk $q$. Hasonlóan az $A\text{'}CA$ és az $A\text{'}\text{'}B\text{'}\text{'}O$ háromszögek egybevágóak, és területük $q^4$. Következésképp az $A\text{'}A\text{'}\text{'}B\text{'}\text{'}B\text{'}C$ szabályos ötszög területe $1-q^2-2q^4$. Ebből a csillagötszög $t_1$ területét úgy kapjuk meg, hogy levonjuk belőle a $B\text{'}C$ alapú, vonalkázott háromszög területének ötszörösét. Ez a háromszög hasonló az $ABC$ háromszöghöz, melynek területe $T_{ABB\text{'}}-T_{BB\text{'}C}=q^2-q^4$, s hasonlósági arányuk $AB:B\text{'}C=q^2$, tehát a levonandó terület $5q^4\left(q^2-q^4\right)$. Összefoglalva, $\begin{array}{c}{\displaystyle t_1=1-q^2-2q^4-5q^4\left(q^2-q^4\right)=65-29\sqrt[]{5}=0\mathrm{,}15\text{...}\mathrm{.}}\end{array}$ Így a keresett arány $\begin{array}{c}{\displaystyle \frac{T}{10}=3\left(\sqrt[]{5}-1\right)\left(65-29\sqrt[]{5}\right)=0\mathrm{,}571\text{...}\mathrm{.}}\end{array}$ (A Kvant c. folyóirat nyomán.)