Cím:	Helly tételéről
Szerző(k):	Bárány Imre
Füzet:	1981/február, 61 - 66. oldal	PDF  |  MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Helly tételéről   Egy síkbeli halmazt konvexnek nevezünk, ha két pontjával együtt azok összekötő szakaszát is tartalmazza. Síkbeli konvex alakzatra példát szolgáltat a körlemez, egy háromszög, egy egyenes, egy végtelen sáv, egy félsík és az egész sík is. Világos, hogy ha két (vagy akárhány) konvex halmaznak van közös része, akkor ez a közös rész is konvex. A konvex halmazok elméletének egyik alapvető eredménye Helly tétele. E. Helly 1884-ben született Bécsben, a bécsi egyetem tanára volt. 1938-ban Amerikába emigrált, s 1943-ban halt meg Chicago-ban. Helly tétele síkbeli konvex halmazok esetén így szól:   Tétel. Legyen adva a síkon véges sok konvex halmaz. Tegyük fel, hogy közülük bármely háromnak van közös pontja. Ekkor van olyan pont is, amelyet valamennyi halmaz tartalmaz.   Rögtön megjegyezzük, hogy ez a tétel nem lenne igaz, ha csak annyit követelnénk meg, hogy bármely két konvex halmaznak legyen közös pontja, hiszen ha megadunk $n\ge 3$ általános helyzetű egyenest, akkor ezek páronként metszik egymást, de közös pontjuk nincs. Helly tételének bizonyítása során szükségünk lesz az alábbi egyszerű tényre. Akárhogy is legyenek megadva a síkon az $A_1$, $A_2$, $A_3$ és $A_4$ pontok, létezik olyan $B$ pont, amely az $A_1{A}_2{A}_3$, $A_1{A}_2{A}_4$, $A_1{A}_3{A}_4$ és $A_2{A}_3{A}_4$ háromszögek mindegyikéhez hozzátartozik. 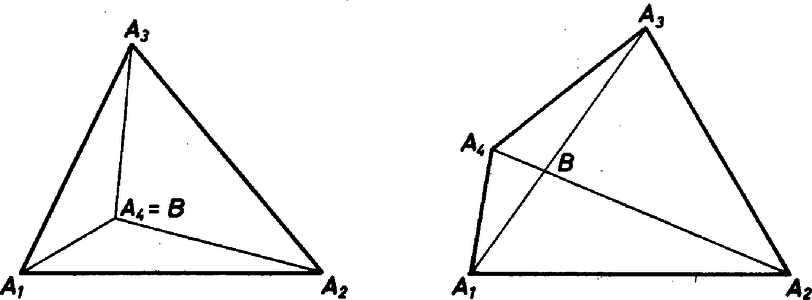  1. ábra   Tegyük föl először, hogy semelyik három pont nem esik egy egyenesre. Ekkor az $A_1$, $A_2$, $A_3$, $A_4$ pontok mint csúcsok vagy egy háromszöget vagy egy konvex négyszöget határolnak körül. Ha háromszöget határolnak, akkor a negyedik pont a háromszög belsejében van és megfelel $B$ gyanánt, ha pedig négyszöget, akkor e négyszög átlóinak metszéspontja választható $B$-nek (1. ábra). ‐ Végül ha három pont, mondjuk $A_1$, $A_2$ és $A_3$ egy egyenesre esnék, és mondjuk $A_2$ a középső, akkor $A_2$ választható $B$-nek.   A tétel bizonyítása. Legyenek $C_1$, $C_2$, $\text{...}$, $C_n$ az adott konvex halmazok. Először az $n=4$ esetre bizonyítjuk a tételt. A $C_2$, $C_3$ és $C_4$ halmazoknak a feltevés szerint van egy $P_1$ közös pontja. Feltehető, hogy $P_1$ nincs $C_1$-ben, mert különben készen volnánk. Hasonlóan választhatjuk a $P_2$, $P_3$ és $P_4$ pontokat úgy, hogy $P_i$ a $C_i$ kivételével mindegyik halmazban benne legyen. $C_1$ tehát tartalmazza a $P_2$, $P_3$, $P_4$ pontokat és ‐ mivel $C_1$ konvex ‐ a $P_2{P}_3{P}_4$ háromszöget is. Hasonlóan $C_2$, $C_3$, illetve $C_4$ tartalmazza a $P_1{P}_3{P}_4$, $P_1{P}_2{P}_4$, illetve $P_1{P}_2{P}_3$ háromszöget. Fenti megjegyzésünk értelmében viszont van olyan $B$ pont, amely hozzátartozik mind a négy háromszöghöz. Következésképpen $B$ közös pontja a $C_1$, $C_2$, $C_3$ és $C_4$ halmazoknak. Ezzel négy halmaz esetére bebizonyítottuk a tételt. A további esetekben teljes indukciót használunk. Tegyük föl, hogy $n\ge 4$ halmaz esetére a tétel érvényes és tekintsük a $C_1$, $C_2$, $\text{...}$, $C_n$, $C_{n+1}$ konvex halmazokat. Tegyük föl még, hogy ezek közül bármely háromnak van közös pontja. Jelöljük $C$-vel $C_n$ és $C_{n+1}$ közös részét, $C$ konvex halmaz. Alkalmazni akarjuk az indukciós feltevést a $C_1$, $C_2$, $\text{...}$, $C_{n-1}$, $C$ halmazokra, ehhez megmutatjuk, hogy közülük bármely háromnak van közös pontja. Ez világos akkor, ha $C$ nem szerepel a három halmaz között. Ha pedig $C$ szerepel, és mondjuk a $C_k$, $C_i$ és $C$ halmazokról van szó, akkor ezek közös része megegyezik $C_k$, $C_i$, $C_n$ és $C_{n+1}$ közös részével. E négy halmaznak viszont van közös pontja ‐ ezt az $n=4$ eset bizonyításakor igazoltuk. Tehát a $C_1$, $\text{...}$, $C_{n-1}$, $C$ konvex halmazok közül is bármely háromnak van közös pontja. Eszerint az indukciós feltevés alkalmazható: e halmazoknak van közös pontja. Ez a pont nyilván benne van a $C_1$, $\text{...}$, $C_{n-1}$, $C_n$, $C_{n+1}$ halmazok mindegyikében. A tételt ezzel igazoltuk. Megjegyezzük, hogy Helly tételének sok bizonyítása ismeretes. Ezekről és a tételével kapcsolatos további eredményekről kiváló áttekintést nyújt az alábbi összefoglaló cikk: Helly's theorem and its relatives, szerzői L. Danzer, B. Grünbaum és V. Klee, megjelent a Proceedings of symposia in pure mathematics VII. kötetében, 1963-ban. E cikk orosz nyelvű fordítása könyv alakban is megjelent. A továbbiakban Helly tételének néhány érdekes következményét ismertetjük.   Tétel. Tegyük fel, hogy adott a síkon véges sok pont úgy, hogy bármely kettő távolsága legfeljebb egységnyi. Ekkor van olyan $\frac{1}{\sqrt[]{3}}$ sugarú körlemez, amely valamennyi pontot tartalmazza. 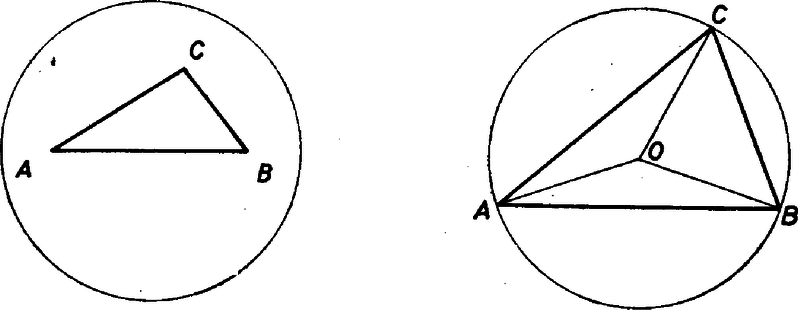  2. ábra   Az állítást először három pont esetén igazoljuk. Legyen tehát adva az $ABC$ háromszög, amelyről tudjuk, hogy minden oldala legfeljebb egységnyi. Ha ez a háromszög nem hegyesszögű, akkor a leghosszabb odalának felezőpontja körül írt $\frac{1}{2}\left(<\frac{1}{\sqrt[]{3}}\right)$ sugarú körlemez lefedi a háromszöget. Ha pedig a háromszög hegyesszögű, akkor tekintsük körülírt körének $O$ középpontját. Az $AOB$, $BOC$ és $COA$ szögek összege ${360}^{\circ }$, valamelyik szög tehát, mondjuk az $AOB\sphericalangle \ge {120}^{\circ }$ (2. ábra). Ekkor a körülírt kör sugara $\begin{array}{c}{\displaystyle AO=\frac{AB}{2}\cdot \frac{1}{\text{sin}\frac{AOB\sphericalangle }{2}}\le \frac{1}{2}\frac{1}{\text{sin}{60}^{\circ }}=\frac{1}{\sqrt[]{3}}\mathrm{.}}\end{array}$ Ez a kör persze lefedi a háromszöget, állításunkat tehát ebben az esetben is igazoltuk. Tekintsük most az általános esetet: Legyenek adva a $P_1$, $\text{...}$, $P_n$ pontok úgy, hogy bármely kettő távolsága legfeljebb egységnyi. Vegyük föl a $P_i$ középpontú, $\frac{1}{\sqrt[]{3}}$ sugarú $K_i$ körlemezt $i=\mathrm{1,}\mathrm{2,}\text{...}\mathrm{,}n$-re. Állítjuk, hogy a $K_1$, $\text{...}$, $K_n$ körlemezek közül bármely háromnak van közös pontja. Legyen $K_i$, $K_j$, $K_k$, a három körlemez. Ezeknek $P$ akkor és csak akkor közös pontja, ha a $P$ pont körüli, $\frac{1}{\sqrt[]{3}}$ sugarú körlemez tartalmazza a $P_i$, $P_j$ és $P_k$ pontokat. Éppen az előbb láttuk, hogy ilyen $P$ pont létezik. Most már alkalmazható Helly tétele a $K_1$, $\text{...}$, $K_n$ körlemezekre, hiszen $K_1$, $\text{...}$, $K_n$ konvex halmazok és közülük bármely háromnak van közös pontja. Eszerint van olyan $O$ pont, amelyik hozzátartozik a $K_1$, $\text{...}$, $K_n$ körlemezek mindegyikéhez. Világos, hogy ekkor $O{P}_i\le \frac{1}{\sqrt[]{3}}$ minden $i=\mathrm{1,}\text{...}\mathrm{,}n$-re, tehát az $0$ körüli, $\frac{1}{\sqrt[]{3}}$ sugarú körlemez tartalmazza a $P_1$, $\text{...}$, $P_n$ pontokat.   Megjegyezzük, hogy a tételben szereplő $\frac{1}{\sqrt[]{3}}$ konstans nem javítható, ugyanis az egységnyi oldalú szabályos háromszög csúcsait kisebb sugarú kör nem tartalmazza. Helly tételének alábbi következménye speciális esetben feladatként szerepelt az 1951. évi Kürschák József emlékversenyen (lásd Matematikai Versenytételek, II. rész, 103. oldal. Tankönyvkiadó, Budapest 1964).   Tétel. Legyen adva véges sok (de legalább három) félsík és egy $C$ konvex halmaz úgy, hogy a félsíkok együttesen lefedik $C$-t. (Minden félsíkhoz hozzászámítjuk a határoló egyenesét.) Ekkor ki lehet választani a félsíkok közül hármat úgy, hogy már azok is lefedjék $C$-t.   Legyenek $F_1$, $\text{...}$, $F_n$ az adott félsíkok. Világos, hogy adott félsíkot a teljes síkká kiegészítő félsík konvex halmaz. Jelöljük $F_1$, $\text{...}$, $F_n$ kiegészítő félsíkjának $C$-vel vett közös részét rendre $G_1$, $\text{...}$, $G_n$-nel. A $G_1$, $\text{...}$, $G_n$ konvex halmazoknak nem lehet közös pontja, hiszen ezt a közös pontot $F_1$, $\text{...}$, $F_n$ egyike sem fedné le, holott a pont $C$-nek pontja. Helly tétele értelmében tehát van olyan három közöttük, mondjuk $G_i$, $G_j$ és $G_k$, amelyeknek nincs közös pontja. Innen már egyszerűen adódik, hogy az $F_i$, $F_j$ és $F_k$ félsíkok lefedik $C$-t. Ezzel a tételt igazoltuk. 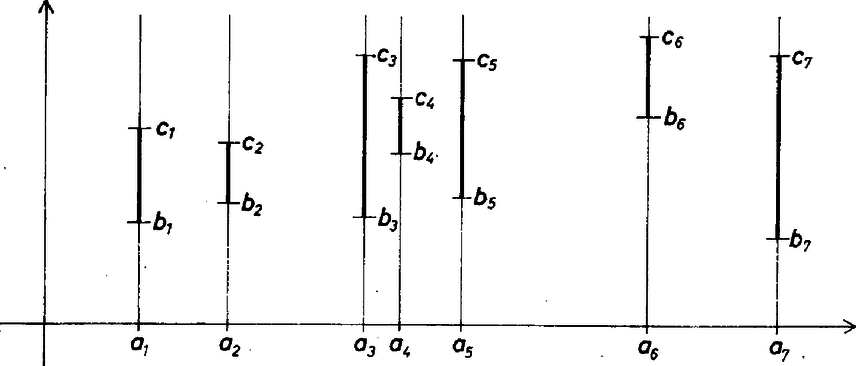  3. ábra   Tegyük fel, hogy egy bizonyos (ismeretlen) függvény értékei az $a_1$, $\text{...}$, $a_n$ helyeken rendre a $\left[b_1\mathrm{,}{c}_1\right]$, $\text{...}$, $\left[b_n\mathrm{,}{c}_n\right]$ intervallumokba esnek. (Úgy gondolhatjuk, hogy ezek az intervallumok mérési eredményekből adódtak.) Tegyük föl továbbá, hogy bármely három intervallumhoz van olyan egyenes, amely metszi mindhárom intervallumot. (Ha az intervallumok "rövidek'', akkor ez úgy tekinthető, hogy a függvény bármely három helyen "jól közelíthető'' lineáris függvénnyel.) A most következő tétel szerint ekkor maga a függvény is "jól közelíthető'' lineáris függvénnyel, legalábbis az $a_1$, $\text{...}$, $a_n$ helyeken. A tételnek ez az interpretációja messzemenő általánosításokhoz vezet (3. ábra).   Tétel. Legyen adva a síkon az $y$ tengellyel párhuzamos intervallumoknak egy véges rendszere. Tegyük föl, hogy bármely három intervallumhoz van olyan egyenes, amely mind a hármat metszi. Ekkor van olyan egyenes is, amely az összes intervallumot metszi.   A bizonyításhoz tekintsük azon egyenesek $E_1$ halmazát, amelyek metszik az első intervallumot, vagyis az ($a_1;b_1$) és ($a_1;c_1$) pontokat összekötő szakaszt. Ezek egyenlete $y=\alpha x+\beta$ alakú, és a mondott feltétel azt jelenti, hogy ${\displaystyle \begin{array}{c}\hfill {\displaystyle b_1\le \alpha a_1+\beta \mathrm{,}}\hfill \\ \hfill {\displaystyle c_1\ge \alpha a_1+\beta \mathrm{.}}\hfill & \text{(<mi>*</mi>)}\end{array}}$ $E_1$ tehát azonosítható a (*) feltételt kielégítő ($\alpha ;\beta$) számpárok ‐ azaz síkbeli pontok halmazával, amelyet szintén $E_1$-gyel jelölünk (4. ábra). 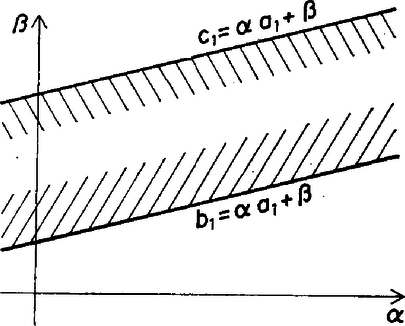  4. ábra   A (*) alatti egyenlőtlenségek egy‐egy félsíkot határoznak meg (ez könnyen ellenőrizhető), az $E_1$ halmaz tehát ‐ mint két konvex halmaz metszete ‐ konvex. Hasonlóan kapjuk az $E_2$, $E_3$, $\text{...}$, $E_n$ konvex halmazokat. A feltétel szerint az $E_1$, $\text{...}$, $E_n$ konvex halmazok közül bármely háromnak van közös pontja, hiszen mondjuk $E_1$, $E_2$ és $E_3$ közös pontja lesz az az ($\alpha ;\beta$) pont, amelyikre az $y=\alpha x+\beta$ egyenes metszi az első három intervallumot. Alkalmazható tehát Helly tétele: van olyan (${\alpha }_0\mathrm{,}{\beta }_0$) pont, amely minden $E_i$-nek eleme. Ez viszont épp azt jelenti, hogy az $y={\alpha }_{0}x+{\beta }_0$ egyenes az összes adott intervallumot metszi. A tétel bizonyítását ezzel befejeztük.   A következő alkalmazás azt mondja ki, hogy egy tetszőleges véges síkbeli $A$ ponthalmaznak van "centruma'', vagyis van olyan $P$ pont, hogy minden $P$-n átmenő egyenes mindkét oldalára "sok'' pontja esik $A$-nak. A bizonyítás Helly tételén kívül felhasználja a konvex burok és az elválasztás fogalmát, így a bizonyítás ismertetésétől eltekintünk.   Tétel. Legyen adva a síkon egy $n$ elemű $A$ ponthalmaz. Ekkor létezik olyan $P$ pont a síkon, hogy minden, a $P$-t tartalmazó félsík $A$-nak legalább $n/3$ pontját tartalmazza. (Most is úgy tekintjük, hogy egy félsíkhoz hozzátartozik a határoló egyenese.) Az 5. ábrán látható példa mutatja, hogy a tételben szereplő $n/3$ nem javítható. 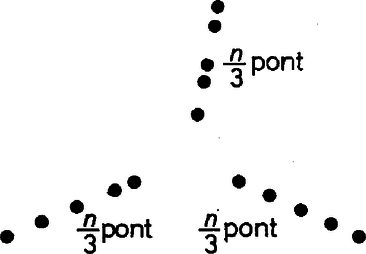  5. ábra   Halmazok konvexitása nemcsak a síkon értelmezhető. Az egyenesnek vagy a térnek egy halmazát konvexnek nevezzük, ha két pontjával együtt azok összekötő szakaszát is tartalmazza. Az egyenes konvex halmazai az intervallumok, a pontok, a félegyenesek és az egész egyenes. Térbeli konvex halmaz például a gömb, a tetraéder, a kúp stb. A tér, illetve az egyenes konvex halmazaira is igaz.   A HELLY‐tétel. Ha a tér (a sík, az egyenes) konvex halmazainak egy véges rendszere olyan, hogy bármely négynek (háromnak, illetve kettőnek) van közös pontja, akkor valamennyi halmaznak is van közös pontja.   E tétel bizonyítása az egyenesen nagyon egyszerű, a térben kicsit nehezebb, de a síkbeli gondolatmenet itt is alkalmazható. Az ismertetett következményeknek is megvan a térbeli (illetve egyenesen vett) megfelelője. Végezetül Helly síkbeli tételének egy olyan általánosítását említjük meg, melyre egyelőre nem sikerült elemi bizonyítást találni, ennek a tételnek egy speciális esete az 1962. gyakorlat (lásd lapunk ezen számának 77. oldalán).   Tétel. Legyen adva síkbeli konvex halmazoknak három véges rendszere, mondjuk piros, kék és zöld halmazok. Tegyük föl, hogy akárhogy veszünk ki egy piros, egy kék és egy zöld halmazt, ezeknek van közös pontja. Ekkor vagy az összes piros, vagy az összes kék, vagy az összes zöld halmaznak van közös pontja.   Ebből a tételből Helly tétele úgy következik, hogy a Helly tételében szereplő konvex halmazokat háromszor vesszük ‐ egyszer piros, egyszer kék és egyszer zöld színűnek tekintve. Magától értetődik, hogy az utóbbi tétel feltételei teljesülnek, következésképpen vagy a piros halmazoknak, vagy a kék halmazoknak, vagy a zöld halmazoknak van közös pontja, de mivel ezek azonosak, az eredeti konvex halmazoknak is van közös pontja.   Bárány Imre (Budapest)