Cím: 1980. A Nemzetközi Fizikaverseny (Helsinki) feladatainak megoldása
Füzet: 1980/november, 161 - 164. oldal  PDF  |  MathML 
Témakör(ök): Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Egy középen alátámasztott, l hosszúságú, homogén szalmaszál függőleges síkban foroghat. A szál eredetileg vízszintes helyzetet foglal el. Egy pók v0 függőleges sebességgel érkezik a szál végétől l/4 távolságban lévő pontba, és azonnal elkezd futni a szálon, úgy, hogy a szál szögsebessége állandó legyen. A pók tömege egyenlő a szalmaszál tömegével. Mekkora lehet v0 maximális értéke, hogy a pók eljuthasson a szalmaszál végéig ? Feltesszük, hogy a pók leesik a szálról, amikor a szál eléri a függőleges helyzetet. Rajzoljuk meg azt a görbét, amelyen a pók mozog !

 

Megoldás. Amikor a pók a szalmaszálra esik, a szalmaszál ω szögsebességgel forgásba jön. Az ω szögsebességet az impulzusmomentum (perdület) megmaradásából számolhatjuk ki.
mv0⋅(l/4)=[Θ0+m(l/4)2]ω,
ahol a bal oldalon az eső pók forgáspontra kiszámított impulzusmomentuma szerepel, Θ0=(1/12)ml2 a szalmaszál, m(l/4)2 a pók tehetetlenségi nyomatéka és ω a szögsebesség. Ebből
ω=12v0/(7l).

A szálnak a szögsebessége a feladat szerint nem változik, annak ellenére, hogy a pók súlya forgatónyomatékot fejt ki. A forgómozgás alapegyenlete alapján az impulzusmomentum változási sebessége egyenlő a forgatónyomatékkal:
d(Θω)/dt=M.
Mivel feladatunkban a szögsebesség nem változik, csupán a Θ tehetetlenségi nyomaték változását kell figyelembe venni:
(dΘ/dt)ω=M.

 
 
1. ábra
 

Az 1. ábra alapján
Θ=Θ0+mx2,
és
M=mgxcosφ.
Ezt behelyettesítve kapjuk, hogy
ω⋅2mx(dx/dt)=mgxcosφ,
ahol φ=ωt és ω=12v0/(7l). Innen
dxdt=7gl24v0cos12v07lt,
ami azt jelenti, hogy a póknak úgy kell haladnia, hogy sebességét mindig a fenti összefüggés határozza meg. Ebből kiszámíthatjuk a pók út‐idő összefüggését. Megkeressük azt a függvényt, amelynek differenciálhányadosa a jobb oldal. Ez a függvény
x=x0+49gl2288v02sin(12v07lt).
Mivel a pók a szalmaszál végétől és így a közepétől is l/4 távolságra esett a szálra, a fenti összefüggésnek t=0 értéknél l/4 értéket kell adnia. Ebből x0=l/4.
Abból a feltételből, hogy a pók a szalmaszál végénél essen le (x=l/2-nél), a szinusz függvény argumentumának π/2-nek kell lennie, mivel ekkor a szál függőleges. v0-át a feltételből meghatározva és visszahelyettesítve az előző egyenletbe, megkapjuk a pálya egyenletét: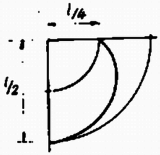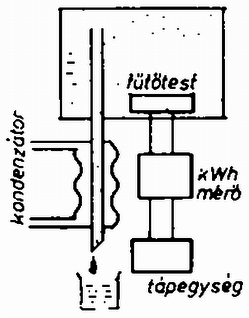
x=l4(1+sin12vt7l)=l04(1+sinφ).
Ezt a pályát mutatja a 2. ábra.
 
 
2. ábra
 
 
3. ábra
 

2. A 3. ábrán látható rendszerben valamilyen folyadék forr különböző fűtőteljesítmény mellett. A kondenzátorban lecsapódó gőzt minden egyes teljesítményszinten 300 másodpercen át gyűjtjük. A táblázat a mérések eredményét tartalmazza. Számítsuk ki a kérdéses folyadék párolgási hőjét. Taglaljuk a hibaforrásokat és azok kiküszöbölésének lehetőségeit !
 

Megoldás: Ha veszteségek nem lépnek fel, a felvett energia és az elfort tömeg között lineális összefüggés van:
Q=Lm,
ahol L a forráshő, amely a forrás hőmérsékletén egyenlő a párolgási hővel.
 

 A feszültség     körülbeli     Energia      Tömegáram   értéke  (k W h)  (g/300 s)(V)  200    0,0237    26,0200    0,0239    28,3200    0,0240    27,9180    0,0191    19,5160    0,0150    14,2140    0,0114     8,8120    0,0083     3,9120    0,0084     4,1120    0,0085     4,2
 

Az első három mérési pontot, mivel a feszültség állandó, ugyanolyan beállításnál vették fel, tehát az eltérést a hibák okozzák. Ezt az állítást az is megerősíti, hogy itt az elforrt tömeg és az energia között nem monoton az összefüggés. Az egyforma beállítási pontokat átlagoljuk.

A 200 V-on felvett pontok átlaga: Energia: 0,02386 kWh; tömegáram: 27,4 g/300 s.
A 120 V-on felvett pontok átlaga: Energia: 0,0084 kWh; tömegáram: 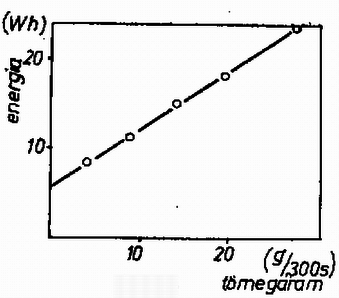4,1 g/300 s.
 
 
 
4. ábra
 

A mérési pontokat a 4. ábrán ábrázoltuk (a 200 V-on, ill. 120 V-on mért értékek fenti átlagát rajzoltuk a grafikonra). A grafikonon egyenest látunk, de ez nem felel meg az (1) összefüggés egyenletének, mivel a tengelymetszet nem nulla. Az illesztett görbe egyenlete
Q=Lm+Q0,
ahol Q0 a veszteség.
A grafikonból
L=2340 kJ/kg;Q0=20,16 kJ.

A véletlen hibákat az azonos feszültségnél felvett pontok tükrözik. Ebből az energia hibája 0,0002 kWh, ami hozzávetőlegesen 1 kJ. Ezt figyelembe véve
L=(2340±50) kJ/kg;Q0=(20±1) kJ.

A Q0 veszteség a mérés szisztematikus hibája. Látjuk, hogy egy pontban történő mérésnél nem tudtuk volna a szisztematikus hibát meghatározni. A feladat lényege éppen abban állt, hogy ezt felismerjük. A veszteség 300 s alatti értéke Q0, így a veszteségi teljesítmény
P0=Q0300 s=(66±3) W
 

3. Toroid alakú vasmag körül a primer tekercsben I1 erősségű áram folyik, amelyet a táblázatban látható lépésekben változtatunk. A primer tekercsben változó áram hatására a szekunderben indukált töltést (Q2) ballisztikus galvanométerrel mérjük. A primer tekercs menetszáma 250, a szekunderé 50. A szekunder tekercs ellenállása 10,0ohm, a ballisztikus galvanométer ellenállása 40,0ohm. Ábrázoljuk a hiszterézis görbét (H‐B, mágneses térerősség ‐ mágneses indukció) ! A toroid közepes kerülete 50,0cm, keresztmetszete 10,0cm2.
(A toroid olyan, mint az autógumi belső. Ha a huzalt egyenletesen tekercseljük a toroidmag köré, mágneses tér csak a gyűrű belsejében van, és értéke H=NI/l, ahol N a menetszám, I az áramerősség, l a toroid közepes kerülete.)
 

  I1  (A)    Q2(⋅10-5 C)  2,0→1,0   -8,0  1,0→0,5   -17,0  0,5→0   -42,0  0→-0,5   -200,0  -0,5→-1,0   -39,0  -1,0→-2,0   -14,0  -2,0→-1,0   +8,0  -1,0→-0,5   +17,0  -0,5→0   +42,0  0→0,5   +200,0  0,5→1,0   +39,0  1,0→2,0   +14,0  
 
Megoldás. Ha I áram folyik a tekercsben, akkor a mágneses tér
H=NI/l,
ahol N a primer tekercs menetszáma (250), l a toroid kerülete (0,5 m), tehát
H=500(l/m)⋅I.

A ballisztikus galvanométerrel mért töltést az indukált áram szállította. Ha a változás Δt idő alatt történt, akkor az átlagos áramerősség
I=Q2/Δt.
Az indukált feszültség (R=Rtekercs+Rgalvanométer=10Ω+40Ω=50Ω):
U=IR=Q2R/Δt.


Ha a mágneses tér változása 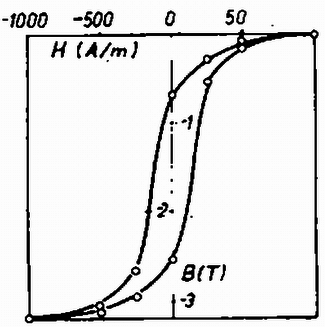ΔB, az indukció törvénye alapján
U=(ΔB/t)FN,
ahol F=10-3 m2 és N=50. Ebből
ΔB=Q2RFN=1kVA m2Q2=1kTCQ2.
Így a táblázatot kiegészíthetjük H és ΔB megfelelő értékeivel.
I1(A)   H(A/m)   Q1(⋅10-5C)ΔB(T)  2,0→1,0  1000→500 -8,0   -0,08 1,0→0,5  500→250 -17,0   -0,17 0,5→0  250→0 -42,0   -0,42 0→-0,5  0→-250 -200,0   -2,00 -0,5→-1,0  -250→-500 -39,0   -0,39 -1,0→-2,0  -500→-1000 -14,0   -0,14 -2,0→-1,0  1000→-500 +8,0   +0,8 -1,0→-0,5  -500→-250 +17,0   +0,17 -0,5→0  -250→0 +42,0   +0,42 0→0,5  0→250 +200,0   +2,00 0,5→1,0  250→500 +39,0   +0,39 1,0→2,0  500→1000 +14,0   +0,14
 
Ezeket az adatokat az A pontból kiindulva ábrázoltuk az 5. ábrán. Az A' pontba tettük a B tengely 0 pontját. Ezzel megkaptuk a vasmag hiszterézis görbéjét.
 
 
5. ábra
 

Kísérleti feladat. Határozzuk meg kísérletileg az adott fonál rugalmas tulajdonságait a húzóerő függvényében! (Az értékelésnél figyelembe vesszük a mérési módszert és az eredmény fontosságát.) A beszámolóhoz mellékeljük a mérési adatokat! Csak a megadott eszközök használhatók.
 

Megoldás. Az adott fonál horgászzsinór volt. A feladathoz több hosszúságmérő eszközt (tolómérce, csavarmikrométer, mérőszalag stb.), akasztható súlyokat, bunzenállványt, a bunzenállványhoz szorítódiókat, több különböző alakú fémdarabot (henger, kocka) mellékeltek.
Ezek segítségével meg lehetett határozni a szál Young moduluszát.
A mérésnél elsősorban az állvány terhelés közbeni lehajlására kellett vigyázni. Ennek hatását különbségi méréssel lehet kiküszöbölni, úgy hogy két szálat függesztünk fel és csak az egyiket terheljük, és hosszkülönbséget mérünk.
A horgászzsinór terhelés nélkül nem egyenes, ezért alapterhelést kellett alkalmazni.
A súly ráakasztásakor a horgászzsinór nem tágult ki azonnal a végleges értékre, ehhez a 3‐4 s-os megnyúlási időt ki kellett várni, vagy azonnal kellett mérni. Az első eset egy sztatikus, a második a dinamikus Young moduluszt adja. A tágulási idő kimérése emelte a mérés színvonalát.
A zsinór megnyúlása nem volt a terhelés egyértelmű függvénye. Pontosabb mérésekkel hiszterézis görbét is ki lehetett mérni.