| Cím: | 1980. évi fizika OKTV feladatai | ||
| Füzet: | 1980/október, 81 - 87. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | OKTV | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az I. forduló feladatai 1. Kulcsot húzunk vékony hengeres rúdra. Állítsuk a rudat lejtősen, de csak annyira, hogy a kulcs még ne csússzék le rajta (1. ábra). Ha most a rudat hossztengelye körül megforgatjuk, a kulcs lecsúszik. a) Magyarázzuk meg a jelensége! b) Mekkora hajlásszög esetén nem csúszik le a kulcs? (Párkányi László) 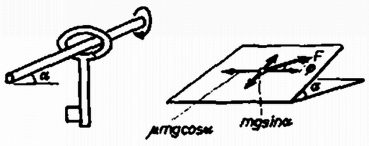 Osztással kapjuk: . Feladatunkban a mozgó rúd felszíne vízszintesen fejt ki erőt, és így sohasem tudja egyensúlyozni az lefelé vivő összetevőt, így a kulcs a rúd megforgatásakor akármilyen kicsi szög esetében is elindul lefelé. (Holics László) 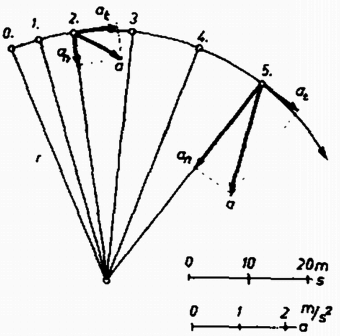 Megoldás. Mivel a pálya mentén megtett út , a sebesség nagysága és a tangenciális gyorsulásösszetevő (2. ábra). A normális gyorsulásösszetevő . A teljes gyorsulás ezekből a paralelogramma-tétellel számítandó: (Vermes Miklós) 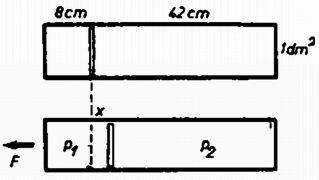 Megoldás. A dugattyút a légnyomások különbségéből eredő erő gyorsítja. Az egész berendezés gyorsulása (a levegő tömege elhanyagolható): Mivel a dugattyút a nyomáskülönbségből származó erő gyorsítja: . Boyle-Mariotte törvénye mindegyik gázra: Felhasználva az előbbi egyenletet: A megoldás: cm és a nyomások: . (Vermes Miklós) 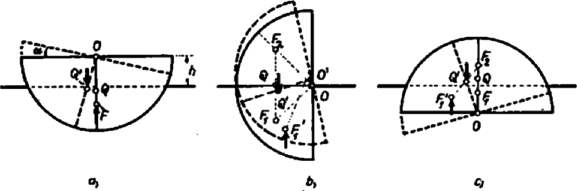 Megoldás. Először ússzék a félgömb vízszintes lapjával felfelé (4.a ábra). A félgömb súlypontja a félgömb szimmetriatengelyén van, a félgömb víz alatti szeletének, vagyis a kiszorított víznek a súlypontja pedig -ben a víz alatti térrész szimmetriavonalán van. A félgömb térfogatát felezi a vízszint folytatásában rajzolt sík. A súly és felhajtóerő egyenlő nagy, hatásvonaluk egy egyenesre esik. Ha a félgömb szöggel kibillen, súlypontja -be kerül, de ugyanott marad (hiszen a vízbe merülő rész ugyanakkora marad), így a testre ható forgatónyomaték a félgömböt visszaviszi eredeti helyzetébe. Ez az egyensúlyi helyzet tehát stabilis. Tekintsük azt az esetet, amikor a félgömb sík lapjával lefelé került a vízre (4.c ábra). A vízvonal ismét felezi a félgömb térfogatát, ezért a víz alatti rész és a kiemelkedő rész súlypontjai egyenlő távolságra vannak a félgömb súlypontjától. Ha a félgömb kibillen helyzetéből, súlypontja -be kerül. A víz alatti rész alakja megváltozik és így súlypontjának helye is. Az súlypont most a egyenesen lesz, mégpedig úgy, hogy , mert a víz alatti és vízből kiálló térfogatrészek egyenlők. A súly és felhajtóerő most is olyan erőpárt hoz létre, amely visszaforgatja a félgömböt régi helyzetébe, azaz ez az egyensúlyi helyzet is stabilis. Vizsgáljuk meg azt az esetet, amikor a félgömb sík lapja merőleges a víz szintjére (4.b ábra). Ekkor a térfogatfelezés miatt a gömb középpontja a víz szintjén van. A negyedgömbök és súlypontjai a félgömb súlypontján átmenő függőleges egyenesen vannak. Most is egyensúlyi helyzettel van dolgunk, mert a súly és a felhajtóerő egyenlő nagy és egy egyenesbe esik. Ha a félgömb kibillen, akkor is, is jobbra kerül, de nagyobb darabbal, mert nagyobb sugarú körön mozog. Olyan forgatónyomaték jön létre, amely átbillenti a félgömböt egyik stabilis helyzetébe, azaz ez az egyensúlyi helyzet labilis. Néhány érdekességet még fel lehet sorolni. Kiindulva valamelyik stabilis egyensúlyi helyzetből egy bizonyos szögig az középpont ugyanolyan magasan marad a vízszint felett, de ha a félgömb alapjának egyik széle víz alá kerül, a középpont magassága csökken, majd a -os helyzetben nulla lesz. A kiemelkedést numerikusan közelítve kell számítanunk, mert a víz alatti rész térfogtának képletét ilyen esetben nem tudjuk felírni. Az 5. ábra felső görbéje ilyen számítás eredményeként mutatja a bemerülési mélységet. -ig változatlanul , azután csökken, majd szimmetrikusan változik, amikor a síklap kerül a víz alá. További numerikus feladat a vízbe merült rész súlypontjának megkeresése és a forgatónyomaték számítása. Ennek eredményét mutatja az 5. ábra alsó görbéje. 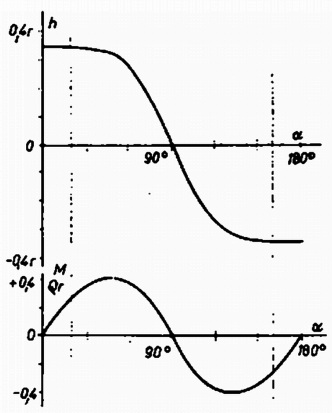 Lényegében ugyanilyenek az egyensúlyviszonyok, ha félgömb helyett bármilyen gömbszeletről van szó és a sűrűség nem . A II. forduló feladatai 1. Egy golyó nagy sebességgel merőlegesen nekigurul a függőleges falnak és hirtelen visszapattan. a) Határozzuk meg azt a legnagyobb magasságot, ameddig a golyó kedvező körülmények között felpattanhat! b) Milyen feltétel következik ebből a súrlódási együtthatóra? (Nagy László) Megoldás. Az sugarú, tömegű, tehetetlenségi nyomatékú golyó sebességgel gurulva érkezik a falhoz, gurulása közben szögsebessége (6. ábra). A falhoz érkezve igen rövid ideig nagy alakváltoztató erő működik . Tegyük fel, hogy az erő az ütközés teljes ideje alatt állandó és, hogy . Az ütközés után legyen a golyó középpontjának vízszintes sebességösszetevője nagyságú, függőleges sebességösszetevőjének nagysága . 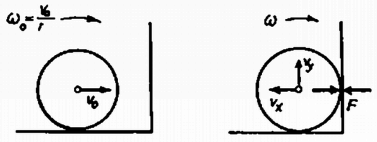 Aszerint, hogy milyen mértékben rugalmas az ütközés és mekkora , az ütközés utáni vízszintes sebességösszetevő nagyságára az alábbi egyenlőtlenség igaz: A vízszintes irányú impulzus megváltozása:
értékének alakulását befolyásolja a súrlódási együttható. értékének olyannak kell lennie, hogy a feltétel teljesüljön. (4)-ből látható, ez akkor teljesül, ha
A súrlódási együttható és a rugalmassági viszonyoktól függő kapcsolatát jobban látjuk, ha (4)-ből kifejezzük a súrlódási együtthatót: 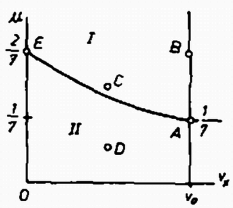 Mi történik akkor, ha kísérleti viszonyaink olyanok, hogy nem tesz eleget az (5) alatti kikötésnek? Egész eddigi gondolatmenetünk azon a feltételezésen alapult, hogy a felfelé futó golyó köszörülése éppen akkor megy át sima gurulásba, amikor a függőleges fallal való érintkezés megszűnik. Ennek feltétele, hogy a pont a 7. ábra görbéjén feküdjön. De mi történik, ha nincs így? Ha a ‐ értékpár pontja a 7. ábra I. mezejébe esik, akkor (a megfelelően nagy súrlódás folytán) a sima gördülés hamarabb áll be, mint az érintkezés megszűnése. A golyó még egy darabig simán gurul tovább, már nem nő tovább és érvényes marad, hogy a legnagyobb emelkedési magasság . Ha ‐ értékpárjának pontja a 7. ábra II. mezejébe esik, akkor nem elég nagy a súrlódás ahhoz, hogy beálljon a sima gördülés, a középpont sebessége még nem érte el a értéket, a maximális magasságot nem érjük el. A legnagyobb emelkedési magasságot tehát akkor érjük el, ha a kísérleti adottságok olyanok, hogy a ‐ értékpárt jelentő pont a 7. ábra vonalára esik vagy annak I. mezejében van és ez a magasság . (Nagy László) Megoldás. Annak nincs semmi akadálya, hogy a tartályokat megfelelő hőtartályokkal különböző hőmérsékleten tartsuk. Azonban a vékony csőösszeköttetés folytán a nyomás a három edényben mindig egyenlő. Ha egy hidegebb gáz nyomása ugyanannyi, mint a melegebbé, ez csak úgy lehetséges, hogy a hidegben nagyobb a molekulasűrűség. Kezdetben a három tartály mindegyikében mól gáz van. A hőmérséklet-változtatás után a tartályok hőmérséklete . A nyomásegyenlőségből következik, hogy a mólszámok fordítva arányosak az abszolút hőmérsékletekkel:
 Az egyenletrendszer megoldása adja a kísérlet végén szereplő mólszámokat: A nyomás kiszámításához gondoljuk meg, hogy a középső tartály hőmérséklete változatlan maradt, de mólszáma 1-ről 0,97-re csökkent. Ugyanilyen arányban kellett a nyomásnak is csökkennie, tehát a kísérlet után a közös nyomás: Az összes gázmennyiség belső energiája a kísérlet előtt: 473 K=30 423 joule. A kísérlet után a teljes gázmennyiség belső energiája: (1) alapján mól 473 K = 459 mól K. Tehát a kísérlet végén is egyenlő a három gázmennyiség belső energiája, de 3%-kal kevesebb, mint előbb. A teljes belső energia: (0,67 joul/gK) joule. A belső energia csökkenése tehát . (Légrádi Imre) 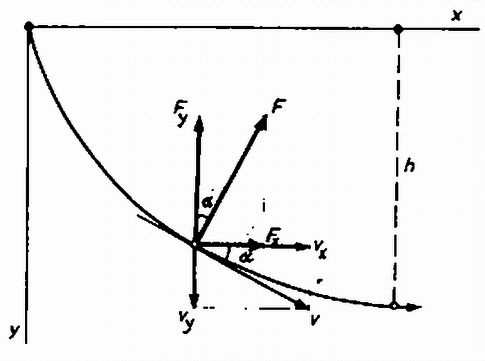 Vizsgáljuk az irányban lejátszódó jelenséget. Az Lorentz-erő vízszintes összetevője: . Azonban a sebesség függőleges összetevője. A gyorsulást és sebességet részletesen felírva: A pálya legalsó pontján mélységben , tehát : 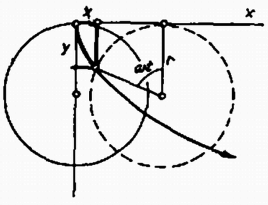 Az eső töltés pályája ciklois. Ezt a következőkkel támaszthatjuk alá. Ha a cikloist létrehozó kör szögsebességgel másodpercig gurul, akkor a ciklois pontjának koordinátái (10. ábra): |