|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Olyan játékokat vizsgálunk, melyekben két személy játszik egymás ellen. Ezeket kétszemélyes, nulla összegű játékoknak nevezik; bennük az egyik fél győzelme a másik vereségét jelenti. A játék során a lépések nem függnek semmiféle véletlen eseménytől, a játékosok szabadon dönthetik el, hogy a megengedett lépések közül melyiket választják. Így vizsgálódásunk köréből kizártuk a szerencsejátékokat. Feltesszük azt is, hogy a játékosok felváltva lépnek, és a játék addigi menetéről mindent tudnak ‐ matematikai szakkifejezést használva a játék teljes információjú. Kimaradnak tehát az alkalmazások szempontjából fontos mátrix-játékok, köztük a jól ismert kő-olló-papír játék is. Ezekről bővebben -ben és -ben olvashatunk. A legtöbb táblás játék, köztük a sakk is, eleget tesz megszorításainknak.
A vizsgált játékok matematikai elmélete meglehetősen egyszerű. A gyakorlatban azonban ‐ ha megpróbáljuk ezt az elméletet közvetlenül alkalmazni ‐ még az egyszerű játékok elemzése is végrehajthatatlanul sok számolást igényel. Így ezekben az analízisekben sok egyedi, egyetlen játékra alkalmazható ‐ idegen kifejezéssel élve ,,ad hoc'' ‐ ötletet találunk. Gondoljunk például a sakkra, használhatók-e más játékok elemzésénél a sokféle megnyitást, végjátékot ismertető vaskos kötetek?
Célunk egy ilyen ad hoc módszernek, a Grundy-számozásnak a bemutatása. Ennek segítségével több olyan játék analízise végezhető el, amelyek egyébként nem, vagy csak igen nagy nehézség árán lennének elemezhetők.
E cikk hét részből áll. Az elsőben pontosan leírjuk a vizsgált játékok struktúráját. A második rész példái a bevezetett fogalmakat illusztrálják. A 3. részben definiáljuk a játékok Grundy-számait, az ezt követő három részben pedig azt mutatjuk be, hogyan használhatók a Grundy-számok annak eldöntésére, hogy a játékban melyik játékos tud nyerni, és ehhez hogyan kell játszania. Végül az utolsó részben egy mindmáig megoldatlan problémát említünk meg.
Természetesen nem volt és nem is állhatott szándékunkban a játékelméletnek ‐ még az általunk választott szűk területének sem ‐ teljes ismertetése. Sok fontos eredményt csak megemlítünk, sokról pedig szó sem esik. A tételek más módon is kimondhatók lennének. A tételek bizonyítása is több helyütt hiányos vagy egészen hiányzik, ám ezeket a hiányokat az érdeklődő Olvasó könnyűszerrel pótolhatja. A cikkben szereplő játékok is a Grundy-számozás alkalmazásait kívánják bemutatni. Így eleve kihagytuk azokat, amelyekre a módszer nem alkalmazható. Kimaradtak azok a játékok is, melyek elemzésénél a Grundy-számozás csak minimális segítséget nyújt, vagy nem kapcsolódik közvetlenül a játék struktúrájához. A megmaradt játékok közül igyekeztünk kiválasztani az érdekesebbeket, és ezek közül is azokat, melyek nem túlságosan bonyolultak.
A cikk megírásához felhasznált legfontosabb forrásmunka J. H. Conway: On numbers and games (Academic Press, 1976) című könyve volt.
1. Milyen játékokról lesz szó ?
Játékaink kétszemélyesek. Úgy képzeljük, hogy valamilyen táblán valamiféle szabály szerint két játékos, akiket Kezdőnek, illetve Másodiknak nevezünk, felváltva lép. A játék folyamán a táblán különféle pozíciók (helyzetek) alakulnak ki, melyek lépésről lépésre változnak, és a játék állását ezek egyértelműen meghatározzák. Játékaink tehát bizonyos pozíciókból állnak, és létezik valamiféle szabály, amely minden pozícióhoz megmondja, hogy a soron következő lépéssel milyen más pozíciók érhetők el, a játékosok mely pozíciókba tudnak lépni. A játékot a Kezdő játékos kezdi, úgy, hogy az egyértelműen meghatározott kezdő pozíció valamelyik (lehetséges) rákövetkezőjét kiválasztja, azaz abba lép. Ezután a Második játékoson a sor: ő választ egyet a Kezdő által választott pozíció rákövetkezői közül, majd ismét a Kezdő következik, és így tovább. A vesztes az, akinek lépnie kellene, de nem tud; más szavakkal: az nyer, aki az utolsót lépi.
Minden játéknak egyetlen kezdő pozíciója van. De tekinthetjük a játék tetszőleges pozícióját is egy rövidebb játék kezdő pozíciójának.
A vizsgált játékok, struktúráját ezek szerint a következőképpen írhatjuk le. Minden egyes pozíciónak megfeleltetünk egy pontot (például a síkban), és ha az pozícióból az pozícióba lehet (közvetlenül) lépni, vagy más szavakkal: ha az rákövetkezője, akkor az -nek megfeleltetett pontból egy nyilat irányítunk az -nak megfeleltetett pontba. Az így kapott struktúrát irányított gráfnak nevezzük, a pozícióknak megfeleltetett pontokat csúcsoknak vagy csúcspontoknak, a nyilakat pedig éleknek.
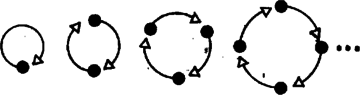
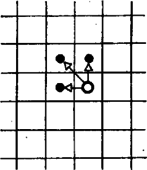
Csak olyan játékokkal foglalkozunk, melyekben véges sok lehetséges pozíció van. Ezek között fontos szerepet játszanak az ún. véges játékok. Egy játék véges, ha akármelyik pozícióból indulnak és akárhogyan is játszanak a játékosok, a játék előbb-utóbb véget ér. Ez azt jelenti, hogy nem találhatók olyan pozíciók, hogy -ből -be, -ből -ba, , -ből -ba és -ból -be lehetne lépni. Speciálisan nem lehet olyan pozíció sem, amely saját magának (egyik) rákövetkezője. A játékoknak megfeleltetett irányított gráfok nyelvén ez a kikötés azt jelenti, hogy a gráf nem tartalmazhatja az 1. ábrán látható gráfok, az ún. irányított körök egyikét sem. Az ilyen gráfot körmentes gráfnak szokás nevezni.
 1. ábra
2. Néhány egyszerű játék
HALOM. Van egy halom valamilyen tárgyunk (babszem, gyufa, érme stb.). A soron következő játékos annyi elemet vesz el a halomból, amennyit akar (akár az összeset is), de legalább egy elemet el kell vennie.
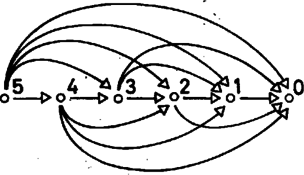
Ez így önmagában egy érdektelen játék, de több összetett játéknak eleme, ezért érdemes vele foglalkoznunk. Kezdő akkor tudja megnyerni ezt a játékot ‐ úgy mondjuk: akkor van nyerő stratégiája ‐, ha a halomban legalább tárgy van. Ha egy tárgy sincs a halomban, akkor Második nyert, mert Kezdőnek lépnie kellene, de nem tud. Legyen a halomban kezdetben tárgy. Ekkor a játéknak összesen lehetséges pozíciója van, attól függően, hogy a halomban vagy elem van-e. A játékhoz tartozó irányított gráfot a 2. ábra mutatja.
 2. ábra
RELATÍV PRÍM. Ismét van egy halom tárgyunk. De most elemből csak akkor vehetünk el elemet, ha és relatív prímek, vagyis az és számoknak nincs -nél nagyobb közös osztójuk.
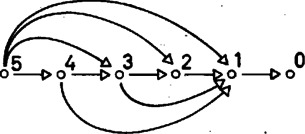
Mindig legalább elemet el kell venni (hiszen semmihez sem relatív prím), pontosan elemet pedig mindig el lehet venni (mert minden számhoz relatív prím). Végül nem lehet egy lépéssel kiüríteni a halmot, kivéve ha csak tárgy van benne, mert esetén az -hez nem relatív prím. Az elemből induló játék gráfja a 3. ábrán látható.
Lássa be az Olvasó, hogy Kezdőnek akkor és csak akkor van nyerő stratégiája, ha kezdetben páratlan sok elem van a halomban !
 3. ábra
LÉTRA. Van egy halom tárgyunk. A soron következő játékos a halomból legalább , de legfeljebb tárgyat vehet el, ahol előre rögzített természetes szám.
Ezt a játékot valószínűleg mindenki játszotta. Másodiknak pontosan akkor van nyerő stratégiája, ha a halom elemeinek száma osztható -gyel. Csak arra kell ügyelnie, hogy minden lépése után is ez a helyzet álljon elő, különben Kezdő nyer.
A következő négy játékot (mondjuk -as) sakktáblán lehet játszani. Kezdetben a tábla jobb alsó sarkában (a mezőn) áll egy bábú, és ezt a játékosok a megadott szabályok szerint felváltva mozgatják. A lépések olyanok, hogy a bábú minden lépésben közelebb kerül a bal felső sarokhoz, s a cél az, hogy oda eljusson. Most is az veszít, aki már nem tud lépni.
 4. ábra
KIRÁLY. A bábuval vagy egy mezővel balra, vagy egy mezővel fölfelé, vagy egy mezővel átlósan balra fölfelé lehet lépni (4. ábra). A nyertes az, aki a bábut a bal felső sarokba tolja, hiszen csak onnan nem lehet tovább lépni.
A játékot Kezdő nyeri. Először átlósan kell lépnie, majd a Második lépéseit utánozva ő jut be a célba.
KIRÁLYNŐ. Léphetünk balra, fölfelé vagy a bal felső csúcsba befutó átló tetszőleges mezőjére (5. ábra).
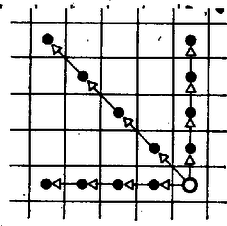 5. ábra
A játékot így természetesen Kezdő nyeri, hiszen első (és egyetlen) lépésével a bábut a bal felső sarokba tolja. Ha azonban a bábu a h4 mezőről indul, akkor Másodiknak van nyerő stratégiája.
BÁSTYA. A bábu az előző játékban leírt módon léphet, csak most az átlós irányú lépés nincs megengedve. A játékban Másodiknak van nyerő stratégiája.
Vegyük észre, hogy a BÁSTYA játék ekvivalens a következővel. Veszünk két, elemű halmot. A soron következő játékos az egyik halmot kiválasztja, és abban a HALOM szabálya szerint lép egyet. Ha a bábu a BÁSTYÁ-ban a balról számított -edik oszlopban és a felülről számított -edik sorban van (), ez megfelel annak az esetnek, mikor az egyik halomban , a másikban elem van. A vízszintes lépések az első halom csökkentésének, a függőleges lépések a második halom csökkentésének felelnek meg.
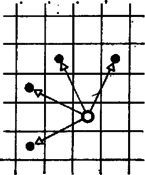 6. ábra
HUSZÁR. A bábu egy mezőről a 6. ábrán látható négy mező valamelyikére léphet, feltéve; hogy az még a táblán van. Ezt a játékot is Második tudja megnyerni.
Az eddigiek mind véges játékok voltak, most lássunk egy nem véges játékot.
DUGÓ (közlekedési). A 7. ábra egy állam térképét mutatja, a városok nevei Abádszalóktól Putnokig futnak. A városokat a térkép szerinti egyirányú utak kötik össze. Egy autó indul Muraszemenyéről, a játékosok egy-egy lépésben valamelyik kivezető úton egy szomszédos városba mehetnek. Az győz, aki Cibakházára beviszi az autót, hiszen (csak) onnan nincs kivezető út.
 7. ábra
A játék nem véges, mert a játékosok körben járhatnak a Muraszemenye ‐ Ipafa ‐ Nagyatád útvonalon. Ennek ellenére Második meg tudja nyerni a játékot. (Hogyan?)
3. Grundy-számok
Az nem-negatív egész számok legkisebb kizártján azt a legkisebb nem-negatív egészet értjük, amely nem fordul elő az számok között. Ezt a számot a legkisebb közös többszörös mintájára jelöli.
Példák: .
Tekintsünk most egy véges játékot. A játék pozícióihoz nem-negatív egész számokat, úgynevezett Grundy-számokat rendelünk a következő szabály szerint:
Azokhoz a pozíciókhoz, melyeknek nincs rákövetkezőjük (azaz amelyekből indulva, a soron következő játékos veszít), -t írunk. Ha egy pozíciónak már minden rákövetkezőjéhez írtunk számot, akkor az pozícióhoz ezek legkisebb kizártja kerüljön.
Egy játék Grundy-száma definíció szerint a játék kezdő pozíciójának Grundy-száma legyen.
Nézzük meg, hogy az előbbi játékok pozícióihoz milyen Grundy-számok tartoznak. Ezek után igazolni fogjuk, hogy minden véges játéknak van Grundy-száma.
HALOM. Egyetlen olyan pozíció van, melynek nincs rákövetkező állapota, azaz amellyel a kitöltést elkezdhetjük: amikor a halomban elem van. Az ehhez a pozícióhoz tartozó Grundy-szám a fenti definíció szerint.
Másodikként az elemet tartalmazó halom Grundy-számát lehet meghatározni. Ennek ugyanis egyetlen rákövetkező pozíciója van, az, amikor a halomban egyetlen elem sincs. A rákövetkezőnek már tudjuk a Grundy-számát, ami , így az elemű halom Grundy-száma .
Két elemű halom esetén a két lehetséges rákövetkező állapot az , illetve a elemű halom. Ezek már kaptak számokat, -et, illetve -t, ezért a elemű halom Grundy-száma .
Általában az elemű halomból kiindulva a Grundy-szám éppen . Ez azt jelenti, hogy a HALOM játék Grundy-száma ‐ ami definíció szerint a kezdő pozíció Grundy-száma ‐ nem más, mint a halom elemeinek száma. Speciálisan a 2. ábrán látható játék Grundy-száma .
RELATÍV PRÍM. Jelöljük az elemből induló játék Grundy-számát -nel. Itt is az első két Grundy-szám (mivel a elemű halomból nem lehet elvenni), illetve . Ha két elemű halomból indulunk ki, az egyetlen lehetséges lépés az egyik elem elvétele. Így nem más, mint .
Három elemű halom esetén akár , akár elemet is elvehetünk, így . Négy elemből csak -et és -at vehetünk el, így . Öt elem esetén maradhat vagy is, innen
Az alábbi táblázat értékét mutatja -ig,
| |
Könnyen igazolható, hogy páros n-re Rn=0, ha n páratlan és n-nek a legkisebb prímosztója éppen a k-adik prímszám, akkor Rn=k. (Az első prím a 2, a második a 3.)
LÉTRA. Az egyszerűség kedvéért a t=3 esettel foglalkozunk, a többi eset hasonlóan intézhető el. Amíg a halomban legfeljebb 3(=t) elem van, addig a LÉTRA és a HALOM játék ugyanaz, tehát az első négy Grundy-szám L0=H0=0,L1=1,L2=2,L3=3. Ha viszont négy elemből indulunk ki, akkor a lépés eredménye nem lehet a 0 elemű halom, tehát L4=lkkz(L3,L2,L1)=lkkz(3,2,1)=0. Öt elemű halom esetén 4,3 vagy 2 elemű halmot kaphatunk, így L5=lkkz(L4,L3,L2)=lkkz(0,3,2)=1. Általában Ln az Ln-1,Ln-2,Ln-3 számok legkisebb kizártja, ami éppen n-nek 4-gyel ‐ általában (t+1)-gyel ‐ való osztásakor kapott maradék.
 8. ábra
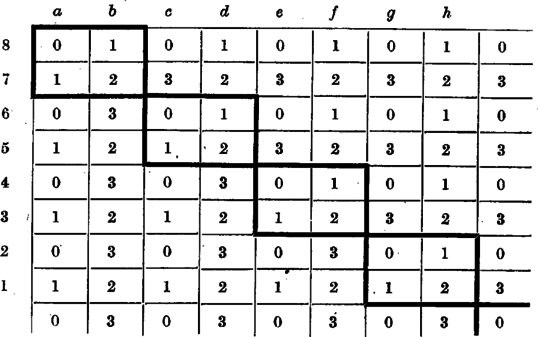
KIRÁLY. A játék pozícióit a sakktábla mezőivel azonosítjuk, a pozíciókhoz tartozó Grundy-számokat a mezőkbe írjuk. A bal felső sarokba 0 kerül, hiszen innen nem tudunk tovább lépni. A felső sor következő mezőjének Grundy-száma lkkz(0)=1, mert ebből a mezőből csak a 0 Grundy-számú sarokmezőbe tudunk lépni. A sor második (c8) mezőjéből csak az előzőbe kerülhetünk, így a beírandó szám lkkz(1)=0. A felső sorban tehát felváltva 0 és 1 áll, ugyanez igaz a bal szélső oszlopra is (8. ábra). Ezek kitöltése után egyetlen mező van, amelynek mindhárom rákövetkezőjét kitöltöttük: a b7 mező. Ebbe a rákövetkezők legkisebb kizártja, lkkz(0,1,1)=2 kerül. A c7 mező száma lkkz(0,1,2)=3, ezt folytatva a második sort ‐ és evvel együtt a második oszlopot is ‐ kitölthetjük. Ha ezekkel végeztünk, rátérhetünk a harmadik sorra stb.
A kitöltést természetesen nemcsak a 8×8-as sakktáblán, hanem akármekkora sakktáblán is elvégezhetjük. A 8. ábrán a vastagon kihúzott kis keretek segítenek a szabályszerűség felismerésében. Ennek alapján tetszőleges méretű sakktábla tetszőleges mezőjének Grundy-számát megmondhatjuk a teljes tábla kitöltése nélkül.
KIRÁLYNŐ. Nem részletezzük a tábla kitöltését, annak kezdő része a 9. ábrán látható. | 01234567891011120453786101192015348671191034562019101287453276901813125340681012712146781910345130278690145314151386710125341516179101112871314151617610119813120151617141811910712142131761815 |
9. ábra
Sajnos nem valószínű, hogy valamilyen egyszerű formula megadná az egyes mezőkbe írandó számokat.
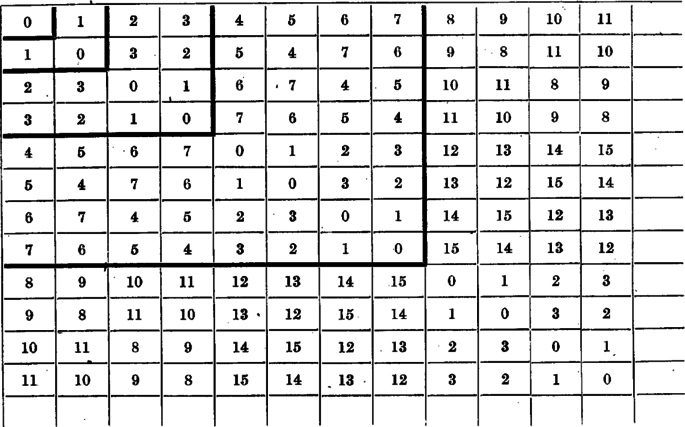
BÁSTYA. Az ehhez a játékhoz tartozó Grundy-számok táblázata a későbbiekben fontos szerepet fog játszani (10. ábra).
A felső sorban a számok 0-tól kezdve 1-esével növekszenek, hiszen a felső sor egy mezőjéről a tőle balra levő mezők bármelyikére (és csak azokra) lehet lépni ‐ ez lényegében azonos a HALOM játékkal. Ugyanez áll a bal szélső oszlopra is. Egy mezőbe akkor lehet a Grundy számot beírni, ha az összes felette álló, valamint az összes tőle balra levő mezőt már kitöltöttük. A mezőhöz tartozó Grundy-szám éppen az ezekben álló számok legkisebb kizártja, azaz a legkisebb olyan szám, amely sem az oszlopában sem a sorában korábban még nem szerepelt.
 10. ábra
A táblázat vastag vonalakkal határolt négyzetei a következő tétel érvényességét mutatják n=1,2,3-ra:
1. tétel. A táblázat bal felső 2n×2n méretű részének minden sorában és minden oszlopában a 0-tól 2n-1-ig terjedő számok mindegyike pontosan egyszer fordul elő.
Legyenek i és j nem-negatív egész számok, és jelöljük i⊕j-vel a balról számított (i+1)-edik oszlop és felülről számított (j+1)-edik sor metszéspontjában álló számot. Például a táblázat szerint 3⊕2=1, valamint 7⊕8=15. A táblázat szimmetrikus a jobbra lejtő átlóra, ezért i⊕j=j⊕i minden (i,j) párra. A felső sorban a számok egyesével növekszenek, tehát 0⊕i=i⊕0=i; az átlóban pedig (legalábbis ameddig a 10. ábra mutatja) csupa 0 áll, így i⊕i=0.
A következő két tétel is a BÁSTYA játék táblázatáról szól.
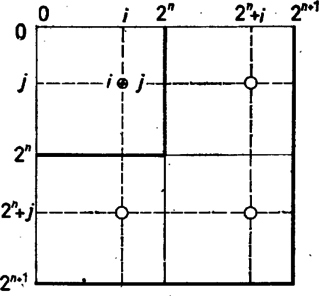
2. tétel. Legyen 0≤i;j<2n. Ekkor (i+2n)⊕j=i⊕(j+2n)=(i⊕j)+2n, valamint (i+2n)⊕(j+2n)=i⊕j (11. ábra).
 11. ábra
Bár mind az első, mind a második tételt önmagában nehéz volna igazolni, a két tételnek egyszerre, n-re vonatkozó indukcióval történő bizonyítása már nem nehéz. Ezt Olvasóinkra hagyjuk, csak úgy, mint annak meggondolását, hogyan következik a 2. tételből a
3. tétel. Írjuk fel i-t, j-t és i⊕j-t is a kettes számrendszerben. Ekkor minden helyi értékre az ott álló három számjegy között páros sok (azaz 2 vagy 0) 1-es található.
A 3. tétel alapján tetszőleges i,j számra viszonylag gyorsan ki lehet számítani az i⊕j számot, és ezt az i és j NIM-összegének nevezzük. Így például ha a 100=11001002 és az 50=1100102 számok NIM-összegét keressük, annak utolsó (kettes számrendszerbeli) helyi értékén 0, az utolsó előttin 1, az azt megelőzőn is 1 stb. áll aszerint, hogy egyezik-e a megfelelő két jegy vagy sem. Így 100⊕50=10101102=86.
Világosabb a NIM-összeadás technikája, ha a számok kettes számrendszerbeli alakját szokásosan egymás alá írjuk (12. ábra).
1100100⊕1100101010110¯
12. ábra
A 3. tételből az is következik, hogy tetszőleges i,j,k nem-negatív egészekre (i⊕j)⊕k=i⊕(j⊕k), azaz a NIM-összeadás asszociatív. Továbbá ‐ mint már sejtettük ‐, i⊕i=0 minden i-re. Ez a korábban megállapított i⊕j=j⊕i és i⊕0=i összefüggésekkel együtt azt jelenti, hogy a nem-negatív egészek erre a műveletre nézve csoportot, mégpedig kommutatív, vagy más néven Abel-csoportot alkotnak. A ⊕ művelet egy érdekessége, hogy inverz művelete saját maga: i-hez j⊕i-t kell NIM-adnunk ahhoz, hogy j-t kapjunk: | i⊕(i⊕i)=i⊕(i⊕j)=(i⊕i)⊕j=0⊕j=j. |
HUSZÁR. A Grundy-számok táblázatán (13. ábra) jól megfigyelhető ismétlődés a 8×8-as táblán még nem tudna kibontakozni. (Kérdés: miért nem fordul elő 4-nél nagyobb szám a táblázatban?)
 13. ábra
Példáinkat befejezve rátérünk egy, már korábban kimondott tétel bizonyítására.
4. tétel. Egy véges játék minden pozíciójának van Grundy-száma.
Tegyük fel az állítással ellentétben, hogy a hozzárendelés szabálya szerint (197. oldal) a játék egyetlen további pozíciójához sem lehet számot rendelni, és mégis van egy X1 pozíció, amelyhez nem került szám. Ez csak amiatt lehetséges, hogy már X1-nek valamely X2 rákövetkezőjéhez sem írhattunk számot. Különben ha X1-nek nem volna rákövetkezője, akkor 0-t, egyébként pedig a rákövetkezőihez írt számok legkisebb kizártját írtuk volna. Ekkor ugyanígy X2-nek is van olyan X3 rákövetkezője, melyhez nem tartozik Grundy-szám, X3-nak is van ilyen X4 rákövetkezője, és így tovább. Ily módon kapjuk az X1,X2,X3,... pozíciókat úgy, hogy mindegyik Xi+1 pozíció az Xi rákövetkezője. Játékunkban azonban csak véges sok pozíció van, tehát ebben a sorozatban valamelyik pozíció ismét előfordul, például Xk=Xi, ahol 1≤k<l. Ám ekkor Xk-ból Xk+1-be, Xk+1-ből Xk+2-be, ... Xi-1-ből Xl=Xk-ba lehet lépni, így gráfunkban létezik kör, azaz a játék nem véges, ellentétben kiinduló feltevésünkkel. Az ellentmondás éppen a tétel állítását bizonyítja.
4. Hogyan lehet egy játékot megnyerni?
Egy (véges) játék pozícióihoz rendelt Grundy-számoknak a következő három fontos tulajdonságuk van:
a) vesztő pozíció Grundy-száma 0;
b) ha egy pozíció Grundy-száma n≥0, akkor egyetlen rákövetkező pozíció Grundy-száma sem n;
c) ha egy pozíció Grundy-száma n>0, akkor a rákövetkező pozíciók között van n-1,n-2,...,1,0 Grundy-számú pozíció is.
Ezekből a tulajdonságokból azonnal adódik az:
5. tétel. Egy véges játékban Kezdőnek akkor és csak akkor van nyerő stratégiája, ha a kezdő pozíció Grundy-száma 0-tól különbözik.
Ha ugyanis a kezdő pozíció Grundy-száma nem nulla, akkor a c) tulajdonság miatt van (esetleg több) 0 Grundy-számú rákövetkezője. Válassza Kezdő ezek valamelyikét. Most Második következik, és 0 Grundy-számú pozícióból indul. Második vagy azonnal veszít ‐ ez az a) eset ‐, vagy pedig kénytelen olyan pozícióba lépni, amelynek Grundy-száma pozitív ‐ b) eset. Következésképp Kezdő ismét pozitív Grundy-számú pozícióból léphet.
Összefoglalva, ha Kezdő eszerint a stratégia szerint játszik, akkor mindig pozitív Grundy-számú pozícióból léphet, aminek a c) tulajdonság miatt feltétlenül van 0 Grundy-számú rákövetkezője. Így Kezdő nem veszthet. S mivel a játék véges, így előbb-utóbb véget ér, Második a vesztes.
Megfordítva, ha a kezdő pozíció Grundy-száma 0, akkor Második érheti el, hogy valahányszor őrá kerül a sor, pozitív Grundy-számú pozícióból léphessen. Így ebben az esetben Másodiknak van nyerő stratégiája.
Ennek a tételnek a segítségével korábbi játékaink mindegyik pozíciójára meg tudjuk mondani, hogy onnan indulva Kezdő vagy Második tudja-e megnyerni a játékot, sőt magát a stratégiát is tudjuk: aki nyerni akar, annak mindig 0 Grundy-számú pozícióba kell lépnie. Ha csak egyszer is téved, ellenfele kezébe adja a nyerés lehetőségét.
Az 5. tétel bizonyítása a Grundy-számoknak az a), b) és c) tulajdonságán, valamint azon a tényen múlott, hogy a játék előbb-utóbb véget ér. A Grundy-számozást és evvel együtt az 5. tételt nem véges játékokra is lehet általánosítani a következő módon.
A Grundy-számok hozzárendelésére a 3. pontban adott eljárást módosítsuk így:
Ahhoz a pozícióhoz,-melynek nincs rákövetkezője, 0-t írunk.
Egy még Grundy-szám nélküli, X pozícióhoz az n≥0 számot a következő esetben rendeljük:
1. ha n a legkisebb kizártja mindazoknak a számoknak, amelyek X megszámozott rákövetkezőihez tartoznak;
2. ha X minden szám nélküli rákövetkezőjének van olyan megszámozott rákövetkezője, melynek Grundy-száma éppen n.
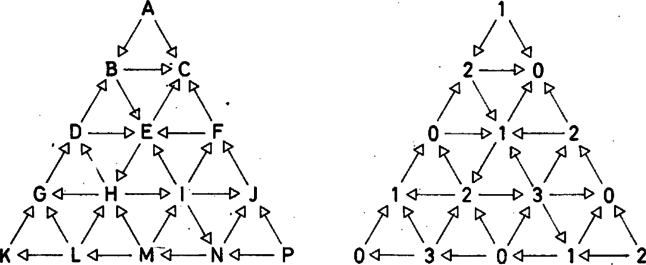
Nézzük, hogyan alkalmazható ez az eljárás a DUGÓ játékra (14. ábra). A C csúcs az egyetlen, amelyből nem indul ki út, így a C csúcs Grundy-száma 0.
 14. ábra
Ezután a D-hez írhatunk 0-t, mert D rákövetkezői B és E még számozatlanok, de mindkettőnek van 0 számú rákövetkezője (a C csúcs). Ezek után G száma 1, hiszen egyetlen rákövetkezőjének, D-nek Grundy-száma 0, és ugyanígy K száma 0.
Most az egyetlen csúcs, amit megszámozhatunk, E, melynek Grundy-száma 1. Valóban, E-nek egyetlen számozott rákövetkezője 0, míg másik, még számozatlan rákövetkezőjéből H-ból eljuthatunk az 1 Grundy-számú G-be. Mivel evvel B mindkét rákövetkezőjét kitöltöttük, B-be lkkz(0,1)=2 kerül, és ezért A-ba lkkz(0,2)=1.
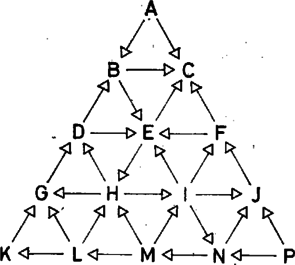
Innen kezdve könnyen meghatározhatjuk az F,J,I,H,L,M,N,P csúcsok Grundy-számait: mire egy csúcsra sor kerül, addigra összes rákövetkezője már kapott számot.
 15. ábra
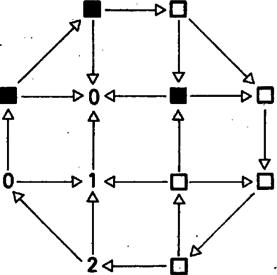
Maradhatnak olyan pozíciók is, melyek még a módosítás alapján sem kapnak számot. Ilyen játék gráfját mutatja a 15. ábra, az üres, illetve teli négyzetek mutatják a ,,számozhatatlan'' csúcsokat. A módosított eljárással kapott Grundy-számok is nyilván rendelkeznek a korábban kimondott a), b), c) tulajdonságokkal, és igaz az 5. tételnek a következő általánosítása:
6. tétel. Egy játékban a Kezdő játékosnak pontosan akkor van nyerő stratégiája, ha a kezdő pozíció valamely rákövetkezője nulla Grundy-számú.
A Második játékosnak pontosan akkor van nyerő stratégiája, ha a kezdő pozíció nulla Grundy-számú.
Minden más esetben mindkét játékos elérheti, hogy ne kapjon ki, azaz ha mindketten ,,okosan'' játszanak, a játék sohasem ér véget.
A 6. tétel bizonyítása hasonló az 5. tétel bizonyításához, csak annál kissé bonyolultabb, szintén az Olvasóra hagyjuk. A 6. tétel alapján a 15. ábra játékát Kezdő nyeri, ha a kezdő pozíció az 1-gyel, a 2-vel vagy a három teli négyzettel jelölt pozíciók valamelyike; Második nyeri, ha a két nullás pozíció valamelyikéből indulnak; végül a játék döntetlen, ha az üres négyzetek bármelyike a kezdő pozíció.
A DUGÓ játéknál a kezdő pozíció az M csúcs, aminek Grundy-száma 0, tehát Másodiknak van nyerő stratégiája. Az a dolga, hogy Kezdő minden lépése után valamelyik 0 Grundy-számú csúcsba irányítsa az autót.
5. Játékok összege
Egy játékot játszani nem mindig nehéz, sőt néha annyira egyszerű, hogy nem is tekintjük igazán játéknak. Mondtuk ezt mindjárt a HALOM-nál. Ám rögtön érdekessé, sőt nehézzé válik, ha több HALOM játékot kell egyszerre áttekinteni, a játékok között valamiféle ,,egyensúlyt'' fenntartani azzal a feltétellel, hogy a soros játékos a rendelkezésére álló több játék közül csak az egyikben léphet. De hogy melyikben, és hogyan, azt már ő dönti el. A vesztes most is az, aki nem tud lépni, azaz aki az utolsónak maradó játékot veszti el.
Hogy könnyebben tudjunk ezekről az összetett játékokról beszélni, egy jelölést vezetünk be. A J1 és J2 játékok összegének nevezzük, és (J1+J2)-vel jelöljük azt a játékot, melyben a soros játékos a J1 vagy a J2 játékok közül pontosan az egyikben lép egyet. Hasonlóan definiáljuk aJ1+J2+J3 stb. összegeket is. Egy összegjáték valamelyik összeadandója lehet maga is egy összeg, ilyenkor azonban a rész-összeadandókat anélkül, hogy előbb külön összeadnánk őket, közvetlen tagoknak is tekinthetjük.
Elsőként nézzük meg, mi történik, ha ugyanazt a játékot vesszük két példányban, vagyis vizsgáljuk a J+J összeget. Ebben Kezdőnek nem lehet nyerő stratégiája. Játsszon ugyanis Második a következőképpen: akármit is lép Kezdő, lépje ő ugyanazt a másik játékban. Így Másodiknak minden lépése után mindkét játék ugyanabba a pozícióba kerül, tehát ha Kezdő tud lépni, tud lépni a Második is. Ha a J játék véges, akkor persze J+J is az, és ekkor J+J-ben Másodiknak van nyerő stratégiája.
Valamivel bonyolultabb a helyzet a J+J+J játéknál. Ha Másodiknak van nyerő stratégiája J-ben, akkor a J+J+J összeget is megnyeri: Kezdő bármelyik játékot is választja, lépje Második ugyanabban a játékban a J-beli nyerő stratégiája szerinti válaszlépést. Így Második a J mindhárom példányát megnyeri, tehát az összeget is.
Ha viszont Kezdőnek van nyerő stratégiája J-ben, és J véges, akkor Kezdő J+J+J-t is meg tudja nyerni. A három J közül az elsőt mintegy szívügyének tekinti, és abban a (J-beli) nyerőstratégiája szerint játszik. Például első lépését is ott teszi meg, és valahányszor Második ebben lép egyet, Kezdő is itt válaszol. A másik két játék csak ráadás: ha Második az egyikben lép valamit, Kezdő lépje ugyanazt a másikban. E szerint játszva Kezdő nem veszthet, s mivel J, és ezzel együtt J+J+J is véges, végül is nyer.
Az a feltétel, hogy J véges, nem hagyható el. Található ugyanis olyan nem véges J játék, amelyben Kezdőnek nyerő stratégiája van, s ugyanakkor J+J+J-t Második akármeddig elhúzhatja.
Az 5. tétel alapján egy véges játékban Másodiknak akkor és csak akkor van nyerő stratégiája, ha a játék Grundy-száma 0. Mivel J-vel együtt J+J,J+J+J,... is véges, az előbbieket kissé általánosítva a következő tételt kapjuk:
7. tétel. Ha a J véges játék Grundy-száma 0, akkor a J+J,J+J+J,... játékok Grundy-száma is 0. Ha a J véges játék Grundy-száma pozitív, akkor a J+J+J,J+J+J+J+J,... játékok Grundy-száma is pozitív, ugyanakkor J+J,J+J+J+J,... Grundy-száma 0.
Ez a tétel egyszerű következménye a következő, első látásra meglepő tételnek, mely azt mondja ki, hogy játékok összegének Grundy-száma kiszámítható a játékok Grundy-számából, s nem függ az összeadandók konkrét struktúrájától.
8. tétel. Legyen a J1 játék Grundy-száma j1, a J2 játéké j2. Ekkor J1+J2 Grundy-száma j1⊕j2, vagyis j1 és j2 NIM-összege.
Bizonyításul csak azt az esetet vizsgáljuk, ha J1 és J2 végesek; az általános eset hasonlóan kezelhető, csak bonyolultabb. A J1+J2 játék pozícióit olyan párokkal ábrázolhatjuk, melyek első tagja a J1 játéknak, második tagja pedig a J2 játéknak egy-egy pozíciója. Ha a J1-beli X pozíció (J1-beli) rákövetkezői X1,X2,...,Xn; a J2 beli Y pozíció rákövetkezői Y1,Y2,...,Ym, akkor a J1+J2 játék (X,Y) pozíciójának összesen n+m rákövetkezője van, és ezek (X1,Y);(X2,Y);...;(Xn,Y), valamint (X,Y1),...,(X,Ym). Az első n pár annak felel meg, mikor a soros játékos J1-ben lép, a második m pedig annak, amikor J2-ben.
Feltevésünk szerint J1,J2 végesek, tehát mindkét játék minden pozíciójához tartozik Grundy-szám. Jelölje az X pozícióhoz tartozó J1-beli Grundy-számot g, az X1,...,Xn pozíciókhoz tartozókat g1,...,gn; a J2 játék Y pozíciójához tartozó J2-beli Grundy-számot h, az Y1,...,Ym pozíciókhoz tartozókat h1,...,hm. Tételünk azt állítja, hogy a J1+J2 játék (X,Y) pozíciójához tartozó Grundy-szám g⊕h. Ezt a Grundy-számok előállítására vonatkozó szabály alapján indukcióval igazoljuk, ebből a tétel állítása azonnal adódik.
Egy pozícióhoz (véges játék esetén) két állapotban írhatunk Grundy-számot: vagy ha a pozíciónak nincs rákövetkezője, vagy ha a pozíció minden rákövetkezőjének már van Grundy-száma. Tekintsük a J1+J2 játék (X,Y) pozícióját. Ennek pontosan akkor nincs rákövetkezője, ha sem X-nek, sem Y-nak nincs rákövetkezője. Ekkor X-nek, Y-nak és (X,Y)-nak is 0 a Grundy-száma, és 0⊕0=0. Erre az esetre tehát igaz az állítás.
Most tegyük fel, hogy a J1+J2-beli (X,Y) pozíció minden rákövetkezőjének már van Grundy-száma, továbbá indukciós hipotézisként tegyük fel azt is, hogy az (Xi,Y) pozíció Grundy-száma gi⊕h, az (X,Yj) pozíció Grundy-száma g⊕hj (itt i≤n;j≤m, és n=0 vagy m=0 is lehetséges). Mivel X és Y Grundy-száma a rákövetkezőihez tartozó számok legkisebb kizártja, azaz | g=lkkz(g1,...,gn),illetveh=lkkz(h1,...,hm), | (1) |
másrészt (X,Y) Grundy-száma | lkkz(g1⊕h,...gn⊕hg⊕h1,...g⊕hm). | (2) |
Ahhoz, hogy tételünket bizonyítsuk, elegendő megmutatnunk, hogy a (2)-ben szereplő érték éppen g⊕h. Ez két dolgot jelent. Egyrészt azt, hogy g⊕h nem fordul elő a zárójelben felsorolt értékek között, másrészt azt, hogy minden (g⊕h)-nál kisebb érték szerepel. Kezdjük az elsővel. Ha g⊕h=gi⊕h volna, akkor ennek mindkét oldalához h-t NIM-adva | g⊕0=g⊕(h⊕h)=(g⊕h)⊕h=(g1⊕h)⊕h=gi⊕(h⊕h)=gi⊕0, |
azaz g=g1 volna, ami (1) miatt lehetetlen. Hasonlóan g⊕h=g⊕hj sem állhat fenn h≠hj miatt. Így g⊕h valóban nem fordul elő (2)-ben a zárójelen belül.
A g⊕h NIM-összeg definíció szerint a (g-1)⊕h,...,1⊕h,0⊕h és a g(h-1),...,g⊕1,g⊕0 számok legkisebb kizártja (10. ábra). Az (1) feltétel szerint a g1...,gn legkisebb kizártja g, így a g1,...,gn között a g-1,...,1,0 számok mind megtalálhatók. Következésképpen (2)-ben a (g-1)⊕h,...0⊕h mindegyike, s ugyanezért a g⊕(h-1),...,g⊕0 mindegyike is szerepel. Így (2) értéke legalább g⊕h, mivel több szám kizártja nem lehet kisebb, mint egy részhalmazuké. De g⊕h nem szerepel közöttük, azért (2) értéke valóban g⊕h. ‐ Ezzel igazoltuk a 8. tételt.
Mindjárt alkalmazzuk is a tételt: a Második játékosnak a J+J játékban nemcsak akkor van nyerő stratégiája, ha J véges; hanem akkor is, ha J kezdő pozíciójának, azaz J-nek van Grundy-száma, mondjuk j. Valóban, J+J Grundy-száma az előző tétel alapján j⊕j=0, ami a 6. tétel alapján Második nyerő stratégiájának létezését tanúsítja. Másodiknak úgy kell lépnie, hogy a két játékban mindig egyforma Grundy-számú pozíciót állítson elő. Ilyen lépésből természetesen több is lehet, de nem feltétlenül vezet ezek mindegyike közelebb a győzelemhez. Például ha két DUGÓ játékot játszanak egyszerre ‐ vagy ami ugyanaz, kezdetben két autó indul ugyanabból a városból (mindegy, hogy melyikből), és egy lépésben az egyik autót vihetik tovább, ‐ akkor Második biztosan nyer.
Minden összeget két tagú összegek összegére bonthatunk fel, a 8. tételt tehát nemcsak két, hanem akárhány játék összegére is alkalmazhatjuk. Ezt tesszük a következő játék elemzésénél.
TRIDUGÓ. A játékot a DUGÓ játék tábláján játssza a két játékos (7. és 14. ábra). Kezdetben egy-egy autó indul az A, a K és a P városból. A soron következő játékos az egyik autót jelenlegi helyéről egy szomszédos városba irányítja. Egy városban egyszerre akár mind a három autó is tartózkodhat. A nyertes az, aki az utolsó autót C-be irányítja (vagyis veszít az, aki nem tud lépni).
A figyelmes Olvasó azonnal észreveszi, hogy ez tulajdonképpen három DUGÓ játék összege. Az egyikben az autó A-ból, a másikban K-ból, a harmadikban pedig P-ből indul. Az egyes játékok Grundy-számai a 14. ábra jobb oldala alapján rendre 1,0, illetve 2, az összegjáték Grundy-száma tehát 1⊕0⊕2=3. Így Kezdőnek van nyerő stratégiája. Egyrészt arra kell ügyelnie, hogy minden lépése után a három autó alatt álló szám NIM-összege 0 legyen ‐ ez könnyű ‐, másrészt arra, hogy a játék befejeződjön, ez már nehezebb. Ez utóbbi cél elérése érdekében célszerű, ha mindig olyan lépést választ, amelyben a mozgatott autó kisebb Grundy-számú pozícióba lép, de persze ez nem elég. Kezdőnek két olyan indulása is van, mellyel az összegjáték Grundy-száma nullává válik: az egyikben az A-beli autót B-be, a másikban a P-beli autót N-be kell irányítania. Ha gyors győzelmet akar elérni, célszerű a második lehetőséget választania, ebben az autó egy 2 Grundy-számú pozícióról egy 1, azaz kisebb számú pozícióba lép. Az A→B lépés viszont több kombinációra ad lehetőséget, talán az ellenfél nagyobb kedvvel veti bele magát a reménytelen küzdelembe.
6. További játékok: a NIM és családja
Több HALOM játék összege a jól ismert NIM játék:
NIM. Van néhány halom tárgyunk. Egy lépésben valamelyik halomból valahány elemet kell elvenni, akár az egész halmot is. A játék nyertese az, aki az utolsó elemet elveszi.
Természetesen a játék Grundy-száma a halmokban található elemek számának NIM-összege, s aki nyerni akar, annak úgy kell játszania, hogy minden lépése után ez az összeg nulla legyen.
A NIM játéknak ezt a formáját és a hozzá tartozó stratégiát Olvasóink bizonyára jól ismerik. Azonban a játéknak több érdekes és kevésbé ismert változata is van. Ezek közül az elsőként bemutatandó változat D. G. Northcott nevéhez fűződik.
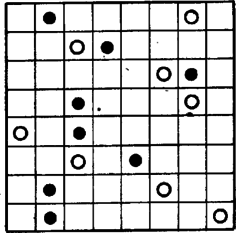
GYALOGOS. A játékot a (8×8-as) sakktáblán a nyolc fehér és a nyolc fekete gyaloggal (paraszttal) játsszák, olyanféle kiinduló állásból, amilyet a 16. ábra mutat. Minden sorban pontosan egy fekete és egy fehér gyalog áll. Kezdő a fehér gyalogokat, Második a feketéket mozgatja úgy, hogy ugyanabban a sorban akárhány mezőt előre vagy hátra léphet, de az ellenfél figuráját nem ugorhatja át, és nem állhat rá az ellenfél mezőjére sem. A vesztes az, aki nem tud lépni, azaz akinek összes figurája ,,beszorult'' (a sor valamelyik végén).
 16. ábra
Annak ellenére, hogy a játék nem véges, lényegében egy ,,bújtatott'' NIM-ről van szó. Benne a halmok elemszámát a szemben álló gyalogok közti üres mezők száma adja meg. Így a bemutatott pozíció Grundy-száma 4⊕0⊕0⊕3⊕1⊕1⊕3⊕5=1. Kezdő tehát nyer, első lépésével a negyediktől a nyolcadik sorig bármelyikben egy mezővel kell közelednie ellenfeléhez. Ha Második hátrál, Kezdő ugyanannyival utánamegy, hogy a figurák közti távolság ne változzék. Ha pedig Második támad, azaz egyik gyalogját közelebb húzza Kezdő megfelelő gyalogjához, akkor a sornak megfeleltetett halmot csökkenti, és Kezdő a NIM játék stratégiája szerint válaszolhat, ami ‐ szükség szerint ‐ ugyanabban vagy egy másik sorban történik meg.
Így Kezdő mindig közeledik ellenfeléhez, egy idő múlva az már nem tud hátrálni, tehát veszít.
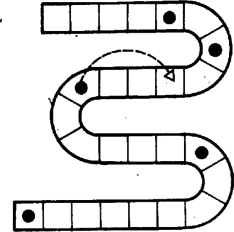
BUBORÉK. Egy fölfelé haladó kanyargós ,,csőben'', amely a 17. ábra szerint mezőkre van osztva, a játékosok elhelyeznek néhány ,,buborékot'', ezeket a sötét körök jelzik. Egy lépésben valamelyik buborékot kell valahány mezővel feljebb tolni. Egy mezőben legfeljebb egy buborék tartózkodhat, és a buborékok nem előzhetik meg egymást. Az ábrán a nyíl egy szabályos lépést mutat. A játék akkor ér véget, amikor az összes buborék a cső tetején gyűlik össze, s a vesztes az, aki már nem tud lépni.
 17. ábra
Ebben a játékban is megtaláljuk a NIM-et. Induljunk el a legalsó buboréktól, és minden páratlan sorszámú buboréktól számoljuk meg az üres mezőket a következőig (illetve páratlan sok buborék esetében utoljára a cső tetejéig). Ezek a számok adják ki a NIM halmok elemszámait, esetünkben ez 7,4 és 4. Mindkét játékos bármelyik ,,halmot'' bármennyivel csökkentheti, s ha egy játékos egy ,,halom'' felső végét megtolja, ellenfele ezt a lépését semlegesítheti az alsó határoló buborék alkalmas megtolásával. Így aki a NIM játékot a fent leírt halmokkal megnyeri, az nyeri meg a buborék játékot is. A bemutatott helyzetben Kezdőnek van nyerő stratégiája, s első lépéseként például a legfelső buborékot tolhatja eggyel feljebb. Ezután a lépés után előálló halmok mérete ugyanis 3,4,7, melyek NIM-összege 0. Jó kezdő lépés az is, ha a legalsó buborékot csatlakoztatja a megelőzőhöz, azaz a 7 elemű halmot teljes egészében elveszi.
FAVÁGÓ. Egy erdőben a fák egy négyzetrács pontjaiban helyezkednek el, bár innen-onnan már hiányzik egy-egy fa (18. ábra). A játékosok felváltva vágják ki (= áthúzzák) a fákat: a soron következő játékos egy vízszintes sorból egyet vagy többet, de csak szomszédosokat vághat ki. A vesztes az, akinek nem marad kivágni való fája.
 18. ábra
Így például Kezdő a felső sorból akár az első négy, akár az utolsó négy fát kivághatja, de nem vehet el mind a két részből, hiszen azok már nem volnának szomszédosak. Maga a játék természetesen nem más, mint az egyes összefüggő fasorokon játszott játékok összege, esetünkben 8 játék összege. Egy összefüggő fasoron a játék lényegében a HALOM játék, azzal a különbséggel, hogy egy vagy több fa kivágásán (elvételén) kívül a megmaradt részt még két különálló részre lehet osztani. Ez azonban nem befolyásolja a játék kimenetelét Annak a játékosnak ugyanis, akinek a NIM játékban nyerő stratégiája van, nem érdeke, hogy növelje a különálló halmok számát. Ellenfele pedig ha az n0,n1,... hosszúságú sorok közül az n0 méretűt néhány közbülső fa kivágásával egy k és egy l hosszúságúra bontja szét, akkor ezzel egy (k⊕l)⊕n1⊕n2⊕..., Grundy-számú pozícióba lép. Ez k⊕l≤k+l<n0 miatt nem lehet nulla, tehát hiába növelte a halmok számát.
A 18. ábra játékának Grundy-száma ezek szerint 4⊕4⊕6⊕2⊕7⊕1⊕3⊕5=4, vagyis Kezdőnek van nyerő stratégiája. Jó kezdő lépés például az, ha a legfelső sorból az első négy fát kivágja.
Ismeretes, hogy a NIM-ben két egyező elemszámú halmot a játékosok bármely lépésük után egyszerűen figyelmen kívül hagyhatnak, hiszen azok együtt a játék kimenetelét nem befolyásolják. Játszhatnának tehát úgy is, hogy külön-külön helyet tartanak fenn az egy elemű, a két elemű stb. halmoknak, és mindegyik helyen legfeljebb egy, annyi elemszámú halom állhat. Amikor lépnek, a változtatandó halmot kiveszik helyéről, elveszik belőle a megfelelő számú elemet, majd visszateszik az új helyére, ha azon a helyen még nem állna halom; illetve ha már áll, akkor az előállított halmot és az ott álló, vele egyező elemszámú halmot is félreteszik ‐ azok már igazában nem vesznek részt a játékban. Vegyük észre, hogy nincs is szükség tárgyakra, halmokra, mindössze azt kell jelölnünk, hogy van-e 1,2 stb. elemszámú halmunk vagy nincs. Ezt az absztrakciós lépést meg is tesszük a következő játékban.
FORDÍTÓ; Van 10 korongunk, mindegyiknek egyik lapja piros, a másik kék. A korongokat a játék elindításául egy sorba rakjuk, néhányat a piros, másokat a kék oldalával felfelé (19. ábra). A soron következő játékos két eljárásból választhat: vagy egy korongot a piros oldaláról a kékre fordít, vagy két korongot fordít meg, de ezek közül a jobb oldali (nagyobb sorszámú) korongot a piros oldaláról a kékre kell fordítania. A vesztes az, aki már nem tud lépni, vagyis az nyer, akinek lépése után minden korongnak a kék oldala látszik.
1 2 3 4 5 6 7 8 9 10 K P P K K K P K K P 19. ábra
A játékban éppen a fent leírt módon bújtattuk el a NIM-et. Az i-edik korong piros fele azt mutatja, hogy van i elemű halmunk; kék fele pedig azt, hogy nincs. Így a FORDÍTÓ játék egy pozíciójának Grundy-számát úgy kaphatjuk meg, ha a piros korongok sorszámait NIM-adjuk össze. A 19. ábra Grundy-száma tehát 2⊕3⊕7⊕10=12. Ebből 0 Grundy-számú pozíciót csak a 10 elemű halomnak 6 eleműre való csökkentésével lehet elérni, tehát az egyetlen nyerő lépés az, ha a 10. és a 6. korongot megfordítjuk.
A NIM-hez hasonló, csak kevésbé ismert játék a
RIM. Van néhány halom tárgyunk. Egy lépésben valamelyik halomból valahány elemet kell elvennünk, de csak annyit szabad, hogy az elvett elemek száma és az elvétel előtti elemek száma relatív prím legyen egymáshoz.
A játék természetesen több RELATÍV PRIM játék összege, így elegendő a RELATÍV PRÍM Grundy-számait ismernünk ahhoz, hogy nyerhessünk.
Hasonló játék a
DIM. Az előzőtől abban különbözik, hogy az elvett elemek száma osztója kell hogy legyen a halomban eredetileg található elemek számának. (Így például bármely halomból akár az összes elemét is elvehetjük.)
Itt is egyetlen játék több példányának összegéről van szó, egyetlen halom esetén a Grundy-számok a következők:
| elemszám 01234567891011121314151617181920Grundy-szám 012131214121312151213 |
Általában, ha az elemszám 2k-nal osztható, de 2k+1-nel már nem, akkor a hozzá tartozó Grundy-szám k+1.
Az előző játékok keveréke a
RIDINIM. Van három halom tárgyunk. Egy lépésben csak az egyik halomból lehet elvenni, mégpedig a következő szabályok szerint. Az első halomból csak annyit, hogy az elvett elemek száma relatív prím legyen a halom elvétel előtti elemszámához (RI), a másikból annyit, hogy az elvett elemek száma osztója legyen a halom elemszámának (DI), a harmadik halomból pedig akármennyit el lehet venni (NIM).
Induljunk ki három 10 elemű halomból. Az első halom Grundy-száma R10=0, a másodiké 2, a harmadiké 10. Tehát Kezdőnek van nyerő stratégiája, s az egyetlen jó kezdő lépése az, ha a harmadik halomból 8 elemet elvesz.
Nemcsak a HALOM játékot, hanem például a LÉTRÁ-t is lehet NIM-szerűen játszani, például a következőképpen.
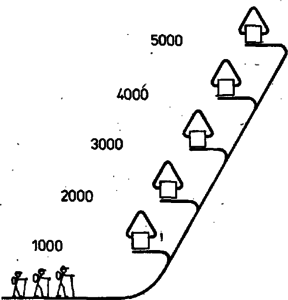
HEGYMÁSZÓ. Három hegymászó egy 5000 méter magas hegyet akar megmászni. A hegyen 1000 méterenként egy-egy menedékház van, a hegymászók ott megpihenhetnek, akár mindhárman egy házban (20. ábra). A három hegymászó közül az egyik még gyakorlatlan, egy alkalommal csak az 1000 méterrel feljebb levő menedékházig képes menni. A második akár 1000, akár 2000 métert tud haladni, míg a legügyesebb a harmadik menedékházhoz is fel tud érni.
 20. ábra
A játékosok felváltva egy-egy hegymászót visznek a mondott megszorításokkal valamelyik magasabban fekvő menedékházba. Az nyer, aki az utolsó hegymászót is a csúcsra viszi.
A játék elemzését az Olvasóra hagyjuk.
7. Oktális játékok, egy megoldatlan probléma
KUGLI. Ezt a játékot H. E. Dudeney (1847-1930) híres angol rejtvényszerző írta le először. A játék alapja egy 14. századbeli népszerű francia labdajáték ‐ a quilles ‐, mely kétségtelenül a mai kugli (és teke) őse. A játékhoz több kuglibábut állítunk fel egy sorba, egymás mellé (21. ábra). A játékosok olyan ügyesek, hogy a kugligolyóval akaratuk szerint bármelyik bábut vagy bármely két szomszédos bábut le tudják dönteni. Egymástól távolabb levő bábukat viszont lehetetlen egyszerre ledönteni. A játékot az nyeri, aki az utolsó bábut dönti le.
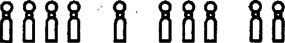 21. ábra
Jelöljük általában dn-nel azt a pozíciót, melyet n egymás mellett álló bábu alkot, és legyen Dn az ehhez a pozícióhoz tartozó Grundy-szám. Például a 21. ábrán látható pozíció nem más, mint d4+d1+d3+d2, és értéke D4⊕D1⊕D3⊕D2. Egy lépés után a dn pozícióból mindazokba, és csak azokba a da+db összeggel jelzett pozíciókba kerülhetünk, ahol a+b vagy (n-1)-gyel vagy (n-2)-vel egyenlő. Ennek alapján a Dn értékeket sorban meghatározhatjuk. Nyilvánvalóan D0=0 és D1=1. A d2 pozíció lehetséges rákövetkezői d0 és d1, így D2=lkkz(D0,D1)=2. Hasonlóan d3 rákövetkezői d1,d2, valamint d1+d1, ez utóbbi azt az esetet jelöli, amikor a három szomszédos bábu közül a középsőt döntjük le. Így D3=lkkz(D1,D2,D1⊕D1)=lkkz(1,2,0)=3. Hasonlóan továbbmenve
D4=lkkz(D2,D1⊕D1,D3,D2⊕D1)=lkkz(2,0,3,2⊕0)=1,D5=lkkz(D3,D2⊕D1,D4,D3⊕D1,D2⊕D2)=lkkz(3,2⊕1,1,3⊕1,2⊕2)=4.
A Dn sorozat elemeit egyre nagyobb n-ekre különösebb nehézség nélkül kiszámíthatjuk. Ezt többen meg is tették, és azt a meglepő tényt fedezték fel, hogy a Dn sorozat periodikus n≥72-re 12 hosszúságú periódussal. A következő táblázatban a Dn értéket 12 hosszúságú sorokba tördelve mutatjuk be, az utolsó sor ismétlődik, az adja a periódust.
Módosítsuk egy cseppet a játékot: mondjuk ki, hogy nem szabad egyetlen bábut ledönteni, mindig két szomszédosat kell eltalálniuk. Természetesen papíron is játszhatunk: egy sorba pontokat rajzolunk.
n012345678910110 012314321426 12 412714321467 24 412854721867 36 412314721827 48 412814721427 60 412814721867 72 412814721827 84 412814721827
A soron következő játékos két szomszédos, még szabad pontot összeköthet.
A vesztes természetesen az, aki nem tud lépni.
Legyen ennél a módosított játéknál az n szomszédos ponthoz tartozó Grundy-szám En. Az En számokat az előzőekben leírtakhoz hasonlóan számíthatjuk ki. Például E0=0,E1=0 (mivel 1 pont esetén is Kezdő veszít), E2=1,E3=1,E4=2 és például | E6=lkkz(E4,E3⊕E1,E2⊕E2)=lkkz(2,1⊕0,1⊕1)=3. |
Az En sorozat is periodikus n≥68-ra, 34 hosszúságú periódussal:
n 0 5 10 15 20 25 30 0 00112 03110 33224 0522330113 02110 4527 344011203110332244552330113021104537 684811203110332244559330113021104537 1024811203110332244559330113021104537
Mindkét játék az úgynevezett oktális játékok családjába tartozik, az első a ⋅77, a második a ⋅07 számhoz tartozó játék. Általában az ⋅A1A2A3... sorozathoz tartozó oktális játék a következő. Ha az Ak≥0 ,,számjegy'' kettes számrendszerbeli alakja éppen 2a+2b+..., ahol a,b stb. egymástól különböző nem-negatív egészek, akkor egy szabályos lépésben bármely rendelkezésre álló halmot k elemmel lehet csökkenteni, majd vagy a vagy b stb. nem üres részre kell szétbontani.
Így, mivel 3=21+20, a ⋅333... játékban bármely halmot akárhány elemmel lehet csökkenteni, és a megmaradó elemekből 1 vagy 0 részt lehet készíteni (azaz az egész halmot is el lehet venni). Ez a játék éppen a NIM.
A ⋅77 esetén 7=22+21+20, így bármely halomból 1 vagy 2 elemet lehet elvenni, és a megmaradt elemeket 0,1 vagy 2 részre lehet osztani. Ha arra gondolunk, hogy az elemek egy sorban állnak, akkor ez éppen azt jelenti, hogy a sorból tetszőleges helyről 1 vagy 2 szomszédos elemet elvehetünk, vagyis éppen Dudeney KUGLI játékát kapjuk.
Általánosabb játékként tekintsük a ⋅156 játékot. Ebben egyetlen elemet akkor vehetünk el, ha az egyedül alkot egy halmot (mivel 1=20); két elemet akkor vehetünk el, ha ezzel vagy az egész halmot elvesszük, vagy a maradékból két további nem-üres halmot csinálunk (mert 5=22+20); végül 3 elemet csak 3-nál több elemű halomból vehetünk el, a maradékot viszont (ha akarjuk) két részre oszthatjuk (hiszen 6=22+21). Ezt a játékot azért mutatjuk be, mert J. C. Kenyon felfedezte, hogy Grundy-számai 3479-től kezdve 349 hosszúságú periódust alkotnak.
A többi oktális játék Grundy-számai hasonlóan viselkednek. Közülük jónéhányat megvizsgáltak és legtöbbjükben a Grundy-számok valahonnan kezdve periodikus sorozatot alkotnak. A véges sok jeggyel leírható oktális játékok közül még egynek a Grundy-számairól sem sikerült megmutatni, hogy nem periodikus sorozatot alkotnak, bár azt sem sikerült igazolni, hogy ezek a sorozatok mindig periodikusak volnának. R. Guy végtelen sok oktális játékról megmutatta, hogy Grundy-számai periodikusak: a ⋅77...777 számú játékban, ha 2k darab (k≥1) hetes szerepel, a Grundy-számok 36⋅2k-tól kezdve 6⋅2k hosszúságú periódust alkotnak.
Az oktális játékok közül az egyik legegyszerűbb, ami tulajdonképpen nem is tekinthető igazán oktális játéknak, P. M. Grundy eredeti játéka. Ebben egy lépésben egy halmot két nem-üres részre kell szétosztani. A játék Grundy-számait számítógéppel több mint negyedmillióig megvizsgálták, és noha sok ,,majdnem-periódust'' találtak, a sorozat nem mutatott periodicitást. Hogy ez a sorozat periodikus-e vagy sem, mindmáig nyitott kérdés.
J. D. Williams: Játékelmélet, Műszaki Könyvkiadó, Budapest, 1972.Neumann János: Válogatott előadások és tanulmányok, Közgazdasági és Jogi Könyvkiadó, 1965.Ilyen játékokat ír le Vargha Balázs: Játékkoktél, Minerva Kiadó, 1967, könyvének 128-294. oldalain. |
 PDF | MathML
PDF | MathML