|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. D. R. Woodall: A négy‐szín tétel
1976. július 22-én Kenneth Appel és Wolfgang Haken, az Illinois Egyetem két matematikusa bejelentette, hogy megoldotta az egész matematika talán legismertebb megoldatlan problémáját, a négy‐szín problémát. A probléma azt kérdezi, vajon ki lehet-e mindig színezni egy tetszőleges térkép tartományait négy színnel úgy, hogy a szomszédos tartományok különböző színűek legyenek. ("Szomszédos'' azt jelenti, hogy "közös határszakaszuk van'', nem követeljük meg, hogy két tartománynak különböző színe legyen, ha azok csak véges sok pontban érintkeznek, mint a és tartományok az 1. ábrán. Azonban a "külső'' tartományt (vagy "tengert'') is ki kell színeznünk, melyet a térkép egy közönséges tartományának tekintünk.)
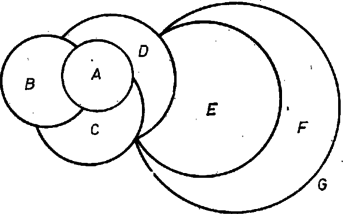 1. ábra
Ezt a feladatot először 1852-ben egy londoni diák, Francis Guthrie vetette fel, és állítólag a kérdés egy Anglia megyéit ábrázoló térkép színezése közben jutott az eszébe. Észrevette, hogy négy színre időnként szükség van (például az 1. ábra , , és tartományainak színezéséhez), de úgy találta, hogy négy szín mindig elegendő. Elmondta ezt a bátyjának, Fredericknek, aki továbbadta tanárának, Augustus De Morgannak (akiről a De Morgan‐törvényt is elnevezték). De Morgan megírta Hamiltonnak, aki azonban kijelentette, hogy őt nem érdekli a kérdés. De Morgannak viszont tetszett a probléma, és minden barátjának elmesélte. Feltételezik, hogy ő jelentette meg a problémát először nyomtatásban, az Atheneum folyóirat egy aláírás nélküli könyvismertetésében, 1860-ban. De Morgan halála után, 1878-ban Cayley ismertette a problémát a Londoni Matematikai Társaság találkozóján, és kijelentette, hogy elképzelése sincs, hogyan lehetne hozzákezdeni a megoldáshoz. Ez felkeltette egy ügyvéd és lelkes amatőr matematikus, A. B. Kempe érdeklődését, aki közben a Londoni Matematikai Társaság pénztárosa, majd elnöke lett. 1879-ben közölt az American Journal of Mathematics-ban egy "bizonyítást'', melyet mindenki jónak hitt. 1890-ben azonban P. J. Heawood, a durhami egyetem matematikaprofesszora talált a "bizonyításban'' egy hibát. Néhány évig a hibát nem tartották komolynak, és úgy tekintették, hogy a tétel "lényegében'' bizonyítva van. Az évek azonban múltak és csak nem talált senki kielégítő megoldást, így a matematikusok fokozatosan felismerték, hogy a probléma sokkal mélyebb, semmint korábban feltételezték. Azóta feltehetően minden neves matematikus próbálkozott a probléma megoldásával, így Appel és Haken teljesítménye mindenképpen elismerésre méltó.
Amint azt egy ilyen feladatnál várni lehet, a megoldás fölöttébb hosszú. Gépelve 100 oldal az összefoglalás, 100 oldal a részletezés és további 700 oldalt tesznek ki a segédtételek, plusz 1200 óra futás számológépen. Összehasonlításul megjegyezzük, hogy a középiskolában (de még az egyetemen is) az átlagos bizonyítások hossza nem haladja meg az egy vagy két oldalt. Az irodalomban egy 20 oldalas bizonyítás már igen hosszúnak számít.
Visszatekintve ‐ bár utólag könnyű okosnak lenni ‐ világos, hogy korábban sokan felettébb alábecsülték a feladat bonyolultságát ‐ de talán senki sem annyira, mint a Clofton College igazgatója. Az volt a szokása, hogy minden szemeszterben egy‐egy versenyfeladatot tűzött ki, és 1866 őszén úgy döntött, hogy a négy‐szín problémát adja fel. A felhívás optimistán végződött: a dolgozat nem haladhatja meg az 1 oldalt (30 írott sor) plusz 1 oldal ábrát. [A versenyfelhívás teljes szövege és a probléma történetének további részletei megtalálhatók a N. L. Biggs, E. K. Lloyd és R. J. Wilson, Graph Theory 1736‐1936. c. könyvben.]
Az igazgató felhívása a Journal of Education-ban is megjelent azzal a szerkesztői megjegyzéssel, hogy "ez a felhívás minden bizonnyal olvasóinkat is a probléma megoldására fogja csábítani''. Az egyik olvasójuk Frederick Temple volt, akkor London püspöke, később Canterbury érseke. Egyszer úgy érezte, kicsit elkalandozhat a figyelme míg a vendégeire vár, és sebtében adott egy " bizonyítást'' a négy‐szín problémára. Ez a "bizonyítás'' azért érdekes, mert rámutat egy gyakori félreértésre a négy‐szín problémával kapcsolatban. Amit Temple valójában bizonyított, az az volt, hogy nem lehet öt tartományt úgy lerajzolni a síkban, hogy bármelyik érintse az összes többit (egy határszakasz mentén). Ezt a problémát 1840 körül Möbius vetette fel, és gyakran összekeverik a négy‐szín problémával. Természetesen van összefüggés a két probléma között: ha valaki tudna találni öt tartományt, melyek mindegyike érinti a többit, akkor egyúttal a négyszínsejtést is megcáfolná, hiszen ezeket csak öt színnel lehetne kiszínezni.
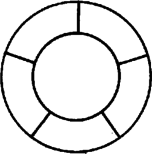 2. ábra
De az, hogy öt ilyen tartomány nem létezik, még nem bizonyítja, hogy a négy‐szín tétel igaz! A 2. ábrán látható térkép színezéséhez négy szín szükséges (tessék kipróbálni!), és mégsem tartalmaz négy tartományt, melyek érintenék egymást. Ez azt mutatja, hogy a térkép színezéséhez szükséges színek száma lehet nagyobb, mint azoknak a tartományoknak a maximális száma, melyek érintik egymást. Így ha be is bizonyítjuk, hogy ez utóbbi szám legfeljebb négy lehet, ez még nem bizonyítja, hogy a térkép négy színnel színezhető.
A bizonyítás vázlata
Csakúgy, mint a többiek, Appel és Haken is a következő átfogalmazás után láttak hozzá a problémához: "Mutassuk meg, hogy egy síkbeli gráf csúcsait ki lehet színezni négy színnel úgy, hogy az éllel összekötött csúcsok különböző színűek legyenek.'' (Egy síkbeli gráf olyan gráf, melyet le lehet úgy rajzolni a síkban, hogy az élei ne messék egymást, lásd például a 3. ábrát.) Nem nehéz látni, hogy a problémának ez a változata ekvivalens az eredetivel. (Az egyik irány könnyű. Vegyünk fel a térképen minden tartomány belsejében egy pontot, és két pontot akkor kössünk össze éllel, ha a megfelelő két tartomány szomszédos. Ha ki tudjuk színezni az így kapott gráf csúcsait négy színnel, akkor természetesen az eredeti térképnek is egy megfelelő színezését kapjuk. A másik irányban azt kell igazolnunk, hogy minden gráfot meg lehet ilyen módon kapni valamilyen térképből. Ez sem túlságosan bonyolult.)
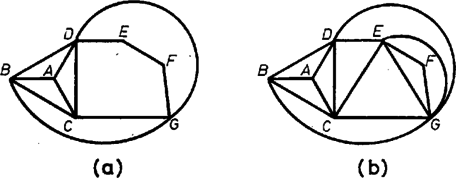 3. ábra
Azt is könnyű látni, hogy elegendő a sík háromszögeléseit tekintenünk, vagyis azokat a gráfokat, amelyek a síkot olyan tartományokra bontják, melyeket pontosan három él határol. Példaképpen a 3. ábra mutatja azt a gráfot, mely az 1. ábra térképének felel meg, és az ebből kapott háromszögelést. Ha ez utóbbi csúcsait négy színnel tudjuk színezni, akkor ez a színezés az előbbihez is jó lesz. Vegyük észre, hogy végeredményben két csúcsot több él is összeköthet (ilyen az és ebben az esetben.)
Kempe bizonyítása
Ahhoz, hogy Appel és Haken módszerét megértsük, érdemes Kempe bizonyítási kísérletét a háromszögelésekre átfogalmazni. Induljunk ki az Euler‐féle poliéder‐tételből, mely azt mondja ki, hogy a sík háromszögelései kielégítik a formulát, ahol a csúcsok száma, az élek száma, a lapok (azaz a tartományok, beleértve a külső tartományt is) száma. Mivel a háromszögelésben minden tartományt három él határol és minden él két laphoz tartozik, azért (az élek "oldalait'' két különböző módon számoltuk le: minden élnek két oldala van, és minden lap három él egy‐egy oldalát tartalmazza). Ha -vel jelöljük az i-edfokú csúcsokat (egy csúcs foka a belőle kiinduló élek száma), akkor (a háromszögelésben található csúcsok száma), és (mivel minden élnek két vége van). Ezeket behelyettesítjük Euler formulájába, és kapjuk, hogy azaz | |
(Egy háromszögelésben nincs 0 vagy 1 fokú csúcs, így nem kellett feltüntetnünk a és az tagokat a fenti összegben.) Azonnal következik, hogy , , és közül legalább az egyik pozitív, azaz a háromszögelésnek a 4. ábrán látható négy konfiguráció valamelyikét mindenképpen tartalmaznia kell. (Vegyük észre, hogy a 3b ábra [kicsit torzítva] tartalmazza mindezeket a konfigurációkat , , , illetve középpontokra ‐ igaz, ezek közül a harmadik quotedblbaseki van fordítva'', és így nehéz felismerni.)  Egy térképet négy színnel kiszínezni néha nagyon nehéz. E. F. Moore készített egy ilyen, 846 országot tartalmazó térképet, ennek egyik felét mutatja az ábra. A teljes térképet úgy kaphatjuk meg, hogy az ábra két példányát egymás mellé illesztjük, és belőlük egy hengerpalástot készítünk. A henger alját és tetejét beragasztjuk, és az így fent és lent keletkező két nyolcszöget (azaz nyolc szomszéddal rendelkező tartományt) is egy‐egy országnak tekintjük. Ennek a térképnek a tanulmányozása segítette Appelt és Hakent a bizonyításukhoz szükséges számítógépidő becslésében.
Tegyük most fel, hogy létezik ellenpélda a négy‐szín sejtésre. Megpróbáljuk ennek lehetetlenségét azzal bizonyítani, hogy valamilyen ellentmondásra jutunk. Válasszunk mindjárt egy olyan ellenpéldát, amelyben a lehető legkevesebb csúcs van. Ha ez nem volna háromszögelés, akkor mindenesetre még hozzávehetnénk további éleket úgy, hogy egy háromszögelést kapjunk anélkül, hogy a csúcsok számát növelnénk, vagy a gráfot négy színnel színezhetővé tennénk. Így minden gráf, melynek kevesebb csúcsa van, mint -nak, négy színnel színezhető, de már nem. Ha a 4a vagy 4b ábrákon látható konfigurációk valamelyikét tartalmazná, töröljük ki -t -ból, a megmaradt gráfot színezzük ki négy színnel és tegyük vissza -t. Mivel legfeljebb három másik csúccsal szomszédos, biztosan találunk neki egy megfelelő színt. Ezzel -t is kiszíneztük négy színnel, ami ellentmond annak a feltételezésünknek, hogy nem négy‐színezhető. Ez az ellentmondás mutatja, hogy valójában nem tartalmazhatja a 4a, illetve 4b alakzatokat.
 4. ábra
A 4c alakzat esetében megpróbálhatjuk ugyanezt, de bajban vagyunk, ha a , , és csúcsok különböző színűek, ebben az esetben nem feltétlenül tudjuk majd -t kiszínezni. Ekkor azonban a következőképpen okoskodhatunk. Tegyük fel, hogy , , és színe ebben a sorrendben kék, zöld, piros és sárga. Nézzük -nak azt a részét, amely az összes kék és piros csúcsból, valamint az őket összekötő élekből áll. Ennek a részgráfnak az összes összefüggő részét (kék‐piros) Kempe‐láncnak hívják (és azt a módszert, amit használni fogunk, Kempe‐lánc módszernek). Ha és különböző (kék‐piros) Kempe‐láncban van, akkor a kék és piros színeket felcserélhetjük abban a láncban, melyben van anélkül, hogy a többi csúcs színét megváltoztatnánk. Ez egy másik (helyes) színezést ad, melyben és mindketten pirosak és így -t kékre színezhetjük. Hasonlóan ha és különböző zöld‐sárga Kempe‐láncban van, akkor megcserélhetjük a zöld és sárga színeket abban a láncban, melyhez tartozik, amivel sárga lesz anélkül, hogy színét megváltoztattuk volna; és így -t most zöldre színezhetjük. Probléma csak akkor van, ha van olyan kék‐piros lánc, ami -t -rel köti össze és egy olyan zöld‐sárga lánc, ami -t az -sel köti össze. De könnyen belátható, hogy ez nem lehetséges, mivel ezeknek a láncoknak valahol metszeniük kellene egymást egy olyan csúcsban, melynek egyszerre kellene kéknek vagy pirosnak és zöldnek vagy sárgának lennie, ami lehetetlen. Így minden esetre megmutattuk, hogy négy színnel ki tudjuk színezni -t, és ez az ellentmondás mutatja, hogy nem tartalmazhatja a 4c konfigurációt sem.
Eddig beláttuk, hogy nem tartalmazhatja a 4a, 4b és a 4c alakzatokat. Ha Kempe meg tudta volna mutatni, hogy a 4d alakzatot sem tartalmazhatja, akkor befejezhette volna a bizonyítást azzal, hogy a (ami a definíció szerint minimális ellenpélda a sejtésre) nem létezhet, hiszen tudjuk, hogy ha létezik, akkor a 4a‐4d konfigurációk valamelyikét tartalmaznia kell. Így igazolta volna, hogy a sejtésre nem létezik ellenpélda, más szavakkal: igazolta volna a sejtést. Sajnos ugyanazt az ötletet próbálta használni a 4d konfigurációra is, amit a 4c-re használt, és itt követte el a hibát. Ennek ellenére jelentős lépést tett a probléma megoldása felé; melyet gyakran alábecsültek a későbbi kutatók. Bár bizonyítása rossz volt (és így gyakorlatilag értéktelen), az ötlet egy kis módosításával egy tökéletesen jó bizonyítást kapunk arra, hogy minden térkép színezéséhez öt szín elegendő, és az ő ötletei szolgáltak alapul a problémával foglalkozó későbbi munkák legtöbbjéhez.
A két fő lépés
Röviden összefoglalva, Kempe módszere modern terminológiával a következő. Megkísérelte, hogy az alakzatoknak egy olyan halmazát állítsa össze (a 4. ábra a‐d részei), melyre
| (i) | az halmaz elkerülhetetlen, azaz minden egyes síkbeli háromszögelés tartalmazza a halmaznak legalább egyik elemét, és |
| (ii) | az halmazban minden egyes elem redukálható, azaz a sejtésre vonatkozó minimális ellenpéldában egyik sem lehet benne. (Más szavakkal egy olyan ellenpélda, amely ezek bármelyikét tartalmazza, egy kisebb ellenpéldává redukálható). |
Ha a kísérlete sikerrel járt volna, nyilvánvalóan elegendő lett volna a sejtés bizonyítására. Valójában nem mutatta meg kielégítően, hogy a 4d konfiguráció redukálható. Appel és Haken ugyanezt a közelítést vitte sikerre. De míg Kempe elkerülhetetlen halmaza mindössze négy alakzatot tartalmazott, addig Appel és Hakené körülbelül 1900-at. (Eredeti bizonyításuk 1939 konfigurációt használt, később megmutatták, hogy ezt mintegy 1400-ra le lehet szorítani.) Annak igazolása, hogy ez a nagyszámú alakzat redukálható, egyelőre a számológépben való nagymértékű bizalomra épül. Egyik alakzatukat az 5. ábra mutatja, ezt egy 12 élből álló gyűrű határolja. A megvizsgálandó alakzatok mindegyikét 14 vagy kevesebb él határolja. Ha nagyobb alakzatokat kellett volna használniuk, a számológépek mai generációjával valószínűleg nem lettek volna képesek bizonyítani azok redukálhatóságát.
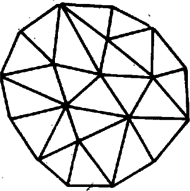 5. ábra
Appel és Haken bizonyítása tehát két lényeges lépésből áll: az alakzatok elkerülhetetlen halmazának megkonstruálásából, és annak bizonyításából, hogy ezek az alakzatok redukálhatóak. Mindkét lépés külön-külön egyszerű, a közöttük levő kapcsolat az, ami bonyolult, és ez az, amiben Appel és Haken munkája minőségileg, és nemcsak mennyiségileg nőtt fölé mindannak, amit előttük csináltak.
Appel és Haken bizonyításának hosszúsága két okból is szerencsétlen. Először is megnehezíti a bizonyítás ellenőrzését. Természetesen egy bizonyítás értéktelen, ha azt nem tudja más matematikus ellenőrizni. Olyan bizonyítást volna jó találni, melyet minél több ember, minél rövidebb idő alatt képes ellenőrizni. Egy nagyon hosszú bizonyítás ellenőrzése várhatóan sokáig várat magára, és a bizonyítás később is csak viszonylag kevés ember számára válik érthetővé. (Természetesen rövid bizonyításoknak is meglehet ez a bajuk.) Ez különösen érvényes azokra az esetekre, mikor a bizonyítás számológépet használ. A számológépeknek a tiszta matematikába való belépése előtt elvileg bárki ellenőrizhetett bármilyen bizonyítást, ha volt hozzá megfelelő felkészültsége és képessége. Most egy további követelmény is fellépett, nevezetesen egy nagy sebességű számológéphez való hozzáférés. Appel úgy becsülte, hogy a bizonyítás részleteinek ellenőrzése mintegy 300 órát tartana egy nagy számológépen. Kevés olyan matematikus van, aki ennyi gépidővel rendelkezik.
Egy hosszú bizonyítás másik nagy hátránya az, hogy nem mutatja meg, miért is igaz az eredmény. Ez különösen igaz az olyan bizonyításokra, melyek nagy számú önálló eset vizsgálatát igénylik, akár használnak számológépet, akár nem. Biztos vagyok benne, hogy sok matematikus egyetért abban, hogy a tételek bizonyítása csak egy eszköz arra, hogy a tiszta matematika célját elérjük, vagyis megértsük, mi van a tételek mögött. Néha egy bizonyítás annyira világos, hogy azonnal érezzük, egyben megmagyarázza a "valódi okát'' annak, miért is igaz az eredmény. Botorság volna azt hinni, hogy minden tételnek van ilyen bizonyítása, a dolog mégis olyan célnak látszik, amelyért érdemes küzdeni. A következő pár évben kétségtelenül sokan fognak dolgozni azon, hogy Appel és Haken bizonyítását rövidítsék, és egyúttal egy világosabb eljárást találjanak. (Valószínűtlennek tűnik azonban, hogy a bizonyításukat annyira le lehetne rövidíteni, hogy ne legyen továbbra is szükség a számológépbe vetett nagymértékű bizalomra.) Természetesen a felsorolt aggályaink egyike sem akadályozhat bennünket abban, hogy elismerjük Appel és Haken érdemeit.
(Fordította: Csirmaz László)
Megjelent a Mathematical Spectrum, Sheffield 11. kötetének 3. számában 1979-ben. |
|
 PDF | MathML
PDF | MathML