Kezdőlap


Cím:	1979. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldása
Szerző(k):	Surányi János
Füzet:	1980/február, 52 - 57. oldal	PDF \| MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Egy konvex gúla alapja páratlan oldalú sokszög, oldalélei egyenlő hosszúak, és a szomszédos oldallapok közti szögek is egyenlők. Bizonyítandó, hogy az alap szabályos sokszög.

Megoldás. Legyen a gúla alapja az

A_{1} A_{2} ... A_{n}

sokszög (

n

páratlan egész szám), az alaplappal szemközti csúcs

B

. Feltétel szerint

A_{1}, A_{2}, ..., A_{n}

egyenlő távol van

B

-től, tehát egy

B

középpontú gömbön helyezkedik el; továbbá az alaplap síkjában is van, tehát rajta van a két felület metszésvonalán, egy körön. Az alaplap tehát húrsokszög.
Elég megmutatni, hogy a sokszög oldalai egyenlők. Valóban, ha ez igaz, akkor összekötve minden csúcsot a körülírt kör középpontjával, egybevágó egyenlő szárú háromszögekre bontjuk a sokszöget (1. ábra). Ebből következik, hogy a sokszög szögei is egyenlők (a háromszögek száraival szemközti szög kétszerese mindegyik).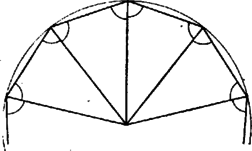

1. ábra

Azt mutatjuk meg, hogy az alaplap második szomszéd oldalai egyenlők. Páratlan oldalú sokszög esetén ebből következik, hogy minden oldal egyenlő, mivel minden oldalról a második szomszédjára térve át páratlan oldalszám esetén bejárjuk az összes oldalt.
Tekintsük az

A_{i} A_{i + 1}

élt felező, rá merőleges

S

síkot. Ez az

A_{i}

-től és

A_{i + 1}

-től egyenlő távolságra levő pontok halmaza. Mivel

B A_{i} = B A_{i + 1}

, így

S

átmegy

B

-n (2. ábra). Ha tükrözünk

S

-re,

A_{i}

és

A_{i + 1}

helyet cserél, az alaplap síkja pedig önmagába megy át, mivel a sík merőleges

S

-re. Ugyancsak önmagukba mennek át a

B

középpontú gömbök is. Ezért önmagába megy át a tükrözéskor az alaplap köré írt kör is.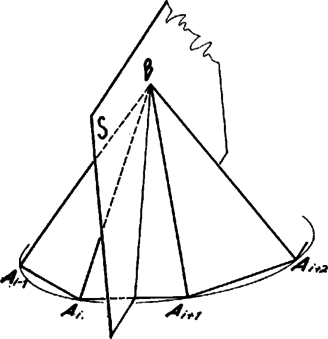

2. ábra

Megmutatjuk, hogy az

A_{i - 1}

csúcs¹ tükörképe

A_{i + 2}

. Jelöljük

A_{i - 1}

tükörképét

C

-vel. Ez is a körülírt körön van. A tükrözés folytán az

A_{i - 1} A_{i} B

és

A_{i} A_{i + 1} B

lapok szöge megegyezik a

C A_{i + 1} B

és

A_{i + 1} A_{i} B

lapok szögével. A gúla konvex volta miatt

A_{i - 1}

A_{i + 2}

és

C

A_{i} A_{i + 1} B

síknak ugyanazon az oldalán fekszik. De az

A_{i + 1} B

egyenes határolta, azt tartalmazó félsíkhoz a határegyenese mentén csak egy olyan félsík illeszthető, amelyik vele adott szöget zár be és az

A_{i} A_{i + 1} B

sík megadott oldalán fekszik (3. ábra). Így

C

és

A_{i + 2}

egy síkban fekszik, rajta van egy nem ebben a síkban levő körön és különbözik a sík és kör

A_{i + 1}

metszéspontjától, tehát kell, hogy egybeessenek.

A_{i - 1} A_{i}

és

A_{i + 1} A_{i + 2}

tehát egymás tükörképei, és így egyenlők. Ez igaz

i = 1,2, ..., n

-re, vagyis az alaplap mindegyik oldala egyenlő a rá következő másodikkal. Mint láttuk, ebből következik, hogy az alap szabályos sokszög.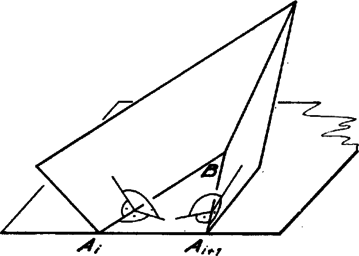

3. ábra

Megjegyzések. 1. Az oldalélek egyenlőségéből már következik a gúla konvex volta, pl. a következők alapján: ha nem volna konvex a gúla, ez azt jelentené, hogy van olyan

P

és

Q

belső pontja, amelyeket összekötő szakasznak van pontja a gúlán kívül. Vetítsük a

P Q

szakaszt az alappal szemközti csúcsból az alap síkjára. A

P' Q'

vetület olyan szakasz volna (4. ábra), amelynek végpontjai az alaplap belsejében vannak, de van az alaplapon kívül levő pontja. Így az alaplap konkáv sokszög volna.

4. ábra

Húrsokszög viszont nem lehet konkáv, hiszen akkor volna a belső szögei közt

180^{\circ}

-nál nagyobb. Annak csúcsa körül elég kis sugarú kört rajzolva ennek a szögtartományba eső (konkáv) körcikke a sokszög belsejében volna (5. ábra). De ennek a körcikknek volna a sokszög köré írt körön kívül eső pontja, márpedig egy húrnégyszögnek nincs a körön kívüli pontja.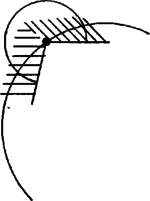

5. ábra

Egy ilyen jellegű bizonyítással azonban nem kívánta a szervező bizottság megterhelni a versenyzők rendelkezésére álló időt.
2. Többen rámutattak, hogy páros oldalszámú gúlára nem feltétlenül teljesül a feladat állítása. A legegyszerűbb ellenpélda erre egy téglalap alapú ,,egyenes'' gúla. Az alappal szemközti csúcs merőleges vetülete a téglalap középpontja. Általában tekintsük egy

O

középpontú körbe írt

2 n

oldalú szabályos sokszöget,

(n \geq 2)

és távolítsuk minden második oldalát ugyanannyival a középponttól, majd a szomszédos végpontokat kössük össze (6. ábra). Könnyű látni, hogy az így keletkezett

2 n

-szög szögei is egyenlők. Összekötjük a sokszög csúcsait az

O

pontban a sokszög síkjára emelt merőleges egy

P

pontjával. A keletkezett gúla szomszédos lapjai egyenlő szöget zárnak be, amint az az alapélek felezőpontjában állított, az élre merőleges síkra történő tükrözéssel belátható. A gúla alapja azonban nem szabályos sokszög.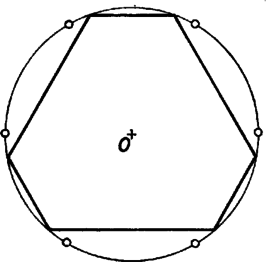

6. ábra

2. feladat. Egy minden valós számra értelmezett

f

függvény minden

(x, y)

értékre kielégíti a következő egyenlőtlenségeket:

\begin{matrix} f (x) \leq x, \\ f (x + y) \leq f (x) + f (y) . \end{matrix}

Bizonyítsuk be, hogy minden valós

x

-re

f (x) = x

I. megoldás. Ha van a feltételeket kielégítő

f

függvény, arra a feltétel első egyenlőtlenségét

x = 0

esetén alkalmazva

\begin{matrix} f (0) \leq 0 \end{matrix}

adódik. A második egyenlőtlenségből

\begin{matrix} f (x) = f (x + 0) \leq f (x) + f (0) . \end{matrix}

Innen viszont

\begin{matrix} 0 \leq f (0), \end{matrix}

tehát csak

f (0) = 0

lehet.
Ismét a második egyenlőtlenség felhasználásával

\begin{matrix} 0 = f (0) = f (x - x) \leq f (x) + f (- x) . \end{matrix}

Másrészt az első egyenlőtlenség alapján

\begin{matrix} f (x) \leq x és f (- x) \leq - x, \end{matrix}

és ezeket összeadva

\begin{matrix} f (x) + f (- x) \leq 0. \end{matrix}

A kettőből

f (x) + f (- x) = 0

f (- x) = - f (x)

.
Végül az első egyenlőtlenségből

\begin{matrix} - f (x) = f (- x) \leq - x, \end{matrix}

tehát

(- 1)

-gyel szorozva

\begin{matrix} f (x) \geq x . \end{matrix}

Ez az első feltételi egyenlőtlenséggel együtt azt adja, hogy a feltételeket kielégítő függvény csak az lehet, amelyik minden

x

értékhez önmagát rendeli.
Erre a függvényre a feladat egyenlőtlenségei valóban teljesülnek, mindegyik esetben egyenlőség áll fenn.

II. megoldás. Kétszer alkalmazva a második, majd kétszer az első feltételi egyenlőtlenséget, a következő összefüggés-sorozatot kapjuk egy, a feltételeket kielégítő

f

függvényre (ha van ilyen):

\begin{matrix} 0 = f (x) - f (x) = f (2 x - x) - f (x) \leq f (2 x) + f (- x) - f (x) \leq \\ \leq f (x) + f (x) + f (- x) - f (x) = f (x) + f (- x) \leq f (x) - x \leq x - x = 0. \end{matrix}

Ez csak úgy állhat fenn, ha minden közbülső kifejezés értéke is

0

, így többek közt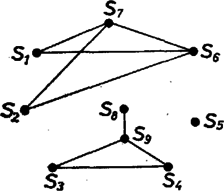

\begin{matrix} f (x) - x = 0, f (x) = x . \end{matrix}

Az így értelmezett függvény valóban kielégíti a követelményeket.

3. feladat. Egy

(n \times n)

-es táblázat minden mezőjében egy betű áll. A táblázat bármely két sora különböző. Bizonyítsuk be, hogy a táblázatnak van olyan oszlopa, amelyiket elhagyva a megmaradó táblázatnak nincs két egyező sora.

I. megoldás. Indirekt úton bizonyítjuk az állítást. Ha a feladat állítása nem volna igaz, akkor minden oszlophoz tartoznék legalább két olyan sor, amelyik csak a kérdéses oszlopbeli betűben különbözik. Minden oszlophoz válasszunk ki egy ilyen sorpárt. Ezt a kiválasztást szemléltethetjük úgy, hogy az

i

-edik sort egy

S_{i}

ponttal ábrázoljuk, és ha az

i

-edik és

j

-edik sor egy kiválasztott sorpár, akkor az

S_{i}

és

S_{j}

pontot összekötjük egy vonallal (7. ábra). Ezeket a vonalakat élnek fogjuk nevezni, az egész ábrát pedig gráfnak. Gráfunknak

n

pontja van és ugyanannyi éle. Egy ilyen gráfban mindig van kör, vagyis olyan, különböző pontokból álló

S_{i_{1}}, S_{i_{2}}, ..., S_{i_{k}}

sorozat, amelyben

S_{i_{j}}

-t

S_{i_{j + 1}}

-gyel

(i = 1, ..., k - 1)

és

S_{i_{k}}

-t

S_{i_{1}}

-gyel él köti össze. Ha ugyanis egy

n

-pontú gráfban nincs kör, akkor annak legfeljebb

n - 1

pontja lehet. Ezt a megoldás a végén bizonyítjuk.

7. ábra

A fenti kör a táblázatra vonatkozóan azt jelenti, hogy az

i_{1}

-edik és

i_{2}

-edik sor csak egy betűben, mondjuk a

j

-edik oszlopbeliben különbözik, az előbbiben itt egy

a_{1}

, az utóbbiban egy ettől különböző

a_{2}

betű áll. Az

i_{2}

-edik és

i_{3}

-adik sor is csak egy betűben különbözik, és ezek egy másik oszlopban állnak, tehát az

i_{3}

-adik sor

j

-edik betűje szintén

a_{2}

. Hasonlóan az

i_{4}

-edik,

...

i_{k}

-adik sor

j

-edik betűje is

a_{2}

, de az

i_{k}

-adik és

i_{1}

-edik sor is csak egy betűben tér el, és ezek is egy, a

j

-ediktől különböző oszlopban állnak, így az

i_{1}

-edik sor

j

-edik betűje is

a_{2}

kellene, hogy legyen, holott ott az

a_{2}

-től különböző

a_{1}

betű áll. Abból a feltevésből tehát, hogy bármelyik oszlop elhagyásával keletkezik két egyező sor, ellentmondásra jutottunk. Így kell olyan oszlopnak lennie, amelyet elhagyva továbbra is minden sor különböző lesz.

A felhasznált segédtétel bizonyítása:
Egy

n

-pontú gráf egy vagy több összefüggő részből áll, vagyis olyanból, amelyiknek bármelyik pontjából el lehet jutni az összes többibe² (7. ábra). Ha egy összefüggő gráfnak

k

pontja van és nincs benne kör, akkor

(k - 1)

éle van. Gondoljuk a gráfot egy gátrendszer térképének. Minden pontban őrház van egy gátőrrel. Az egyik őrházban van a főőr, aki a többit irányítja (8. ábra). Nyilván minden őr el tud jutni a főőrhöz gátak mentén és csak egyféleképpen, hiszen ha volna két különböző útja is, akkor volna kör is (9. ábra). A főőr kiadja az utasítást (pl. telefonon), hogy mindenki vizsgálja meg a tőle a főőr felé vezető irányban a következő őrházig terjedő gátrészt és jelentse neki, mit tapasztalt. Ő az őrhelyén várja a jelentéseket.

8. ábra

9. ábra

Ekkor egy szakaszt sem vizsgálnak ketten, mert ha ketten vizsgálnák, akkor az egyikük a megszokott útja helyett úgy is eljuthatna a főőrhöz, hogy a kérdéses szakaszra nem lép, hanem az azon feléjövő társát bevárva annak az útját követné (10/

a

ábra). Minden gátszakaszt megnéz valaki, mert ha az egyik végén lakó őr a szakasz érintése nélkül jut el a főőrhöz (vagy ő maga a főőr), akkor a másik végén lakó őr útja csak az lehet, hogy végigmegy a kérdéses szakaszon és utána a szomszédos őr útját követi (10/

b

ábra). Eszerint

(k - 1)

őr minden szakaszt megvizsgál és mindegyiket csak egy gátőr, tehát

(k - 1)

gátszakasz van, vagyis a gráfban

(k - 1)

él. Ezzel bebizonyítottuk az állítást.
Ha egy

n

szögpontú, kört nem tartalmazó gráf több összefüggő részre bomlik, akkor mindegyik részben eggyel kevesebb él van, mint pont, így a gráfnak

(n - 1)

-nél kevesebb éle van.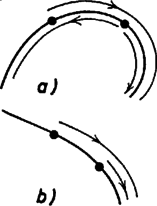

10. ábra

II. megoldás. A következő, a feladatbelinél valamivel általánosabb állítást bizonyítjuk be teljes indukcióval. Ha egy táblázatnak legalább annyi oszlopa van, mint sora, és a táblázat minden mezejére egy betűt írunk úgy, hogy bármely két sor különbözzék, akkor van olyan oszlop, amelyiknek az elhagyása után is különböző sorok különböző módon lesznek kitöltve.
Két sor esetén van legalább két oszlop és van köztük olyan, amelyikben a két sorban különböző betűk állnak. Bármelyik további oszlopot (ha több van, akár mindet együtt is) elhagyhatjuk. Tegyük most fel, hogy

n

-nél kevesebb soros (és legalább ugyanannyi oszlopos) táblázatra igaz az állítás, és vegyünk egy

n

soros táblázatot, amelyik kielégíti az állítás feltételeit. Hagyjuk el az első oszlopot. Ha a sorok ezután is páronként kölönbözők, akkor az állítás igaz. Ha bizonyos sorok így egyenlővé váltak, akkor az egyenlővé vált sorok közül csak egyet-egyet tartsunk meg. Így eggyel fogyott az oszlopok száma és legalább egy sort is elhagytunk, tehát továbbra is legalább annyi oszlop van, mint sor, továbbá bármely két sor különböző. Erre a táblázatra feltevés szerint igaz az állítás: elhagyható egy oszlop úgy, hogy a sorok mind különbözők maradjanak.
Hagyjuk el a megfelelő oszlopot az eredeti táblázatból és nézzünk két sort. Ha mindkettő szerepelt a megritkított táblázatban is, akkor különbözők már akkor is, ha még az első betűket is figyelmen kívül hagyjuk. Ha viszont egy olyan csoportban vannak, amiből csak egy sor került a megritkított táblázatba, akkor az első betűk különbözők. Ekkor is találtunk tehát olyan oszlopot, amelyiknek az elhagyása után bármely két sor különböző maradt. A tulajdonság tehát öröklődik az

n

-soros táblázatokra is.

Megjegyzések. 1. Többen rámutattak, hogy ha csak eggyel is kevesebb oszlop van, mint amennyi sor, akkor már nem bizonyos, hogy van elhagyható oszlop, ami az ábra alapján könnyen belátható.

\begin{matrix} \begin{matrix} a & a & a & a & a \\ b & a & a & a & a \\ b & b & a & a & a \\ b & b & b & a & a \\ b & b & b & b & a \\ b & b & b & b & b \end{matrix} \end{matrix}

2. Sokan az ábécé betűinek a számából próbáltak következtetni. Ez zsákutca volt, hiszen már két jellel is ki lehet tölteni a táblázatot a feltételeknek megfelelően. Egy ilyen kitöltést kapunk, ha az előző megjegyzés táblázatát egy csupa

a

-ból álló oszloppal egészítjük ki.

Surányi János

¹Ha

i = n

A_{i + 1}

-en

A_{1}

értendő,

A_{i + 2}

-n

A_{2}

i = 1

esetén pedig

A_{i - 1}

-en

A_{n}

²Egy-egy ilyen rész állhat egyetlen pontból is.