Cím: "A bűvös kocka matematikája II. rész "
Szerző(k):  Kéri Gerzson 
Füzet: 1980/május, 193 - 198. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A forgatásokkal elérhető állások jellemzői

 

Számozzuk meg a rendezett állapotú bűvös kocka csúcskockáinak és élközépkockáinak külső lapjait 0,1, ill. 2 számjegyekkel, a következőképpen. Jelöljük meg 0 számjeggyel az E és a H lapon levő 8-8 szélső kis négyzetlapot, továbbá az FJ,FB,AJ és AB kockák J és B színű lapjait. Ezután a 0-ás, 1-es és 2-es számjegyeket úgy helyezzük el, hogy minden élközépkocka egyik lapján 0, a másik lapján 1-es számjegy legyen, minden csúcskocka különböző lapján különböző számjegy legyen, ezenkívül teljesüljön még az is, hogy csúcskockák esetén a 0,1,2 számok az órajárás irányában következnek egymás után.
Az E,J és F lapokra kerülő számokat az 1. ábra mutatja. Az egymással átellenes négyzetlapok számozása azonos.
Tetszőleges számú és minőségű forgatás elvégzése után adjuk össze, de külön--külön csak a csúcskockákra, ill. csak az élközépkockákra szorítkozva, a bűvös kocka felületének azokon a helyein levő számokat, ahová a rendezett állású bűvös kockán 0-kat írtunk. Ekkor a csúcskockákra számított összegül 3-mal osztható, az élközépkockákra számított összegül pedig 2-vel osztható eredményt kapunk.
Fenti állításunknak a csúcskockákra vonatkozó része azt állítja, hogy az E és H közepű lapokon a csúcskockák lapocskáin levő számok összege mindig osztható 3-mal. Ehhez elég azt bizonyítani, hogy tetszőleges forgatás hatására a szóban forgó összeg megváltozása osztható 3-mal. Az utóbbi állítás helyessége nyilvánvalóan igaz az E vagy a H közepű lap tetszőleges mértékű elfordítása, továbbá bármelyik lap 180∘-os elforgatása esetén. Ha pedig például a J1 forgatást végezzük el, amely a 4 mozgatott csúcskockát C1-ből C2-be, C2-ből C3-ba, C3-ból C4-be, ill. C4-ből C1-be viszi át (1. ábra), akkor az összeg 6-tal nő, a teljes összeg tehát 3-mal osztható marad. Hasonló gondolatmenet alkalmazható a J,B,A és F lapok tetszőleges irányú 90∘-os elforgatása esetén. Ha azonban már több forgatást hajtottunk végre, egy újabb forgatás hatását lényegesen nehezebb vizsgálni. Ezt az olvasóra hagyjuk, az élkockákra vonatkozó állítás bizonyításával együtt.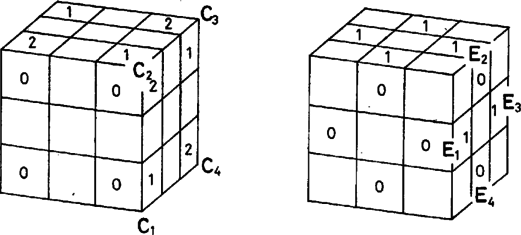
 

 

 
1. ábra

 

A mondott állításokból következik, hogy nem lehet sem csúcskockát, sem élközépkockát helyben forgatni úgy, hogy az összes többi kis kocka változatlan helyen és állásban maradjon,
A következő gondolatmenet alkalmazásához gondolatban számozzuk meg valamilyen módon 1-től 20-ig a csúcskockák és az élközépkockák helyeit, s ugyancsak 1-től 20-ig magukat a a csúcskockákat és az élközépkockákat. A számozásnál csak arra ügyeljünk, hogy a rendezett bűvös kockán minden csúcskocka és élközépkocka a saját sorszámával azonos sorszámú helyen legyen.
Tekintsünk most egy rendezett vagy rendezetlen állapotú kockát, és tegyük fel, hogy i=1,2,...,20-ra az i sorszámú helyen a hi sorszámú kis kocka van. Most képezzük a hi számokból a
h1-h21-2⋅h1-h31-3...h19-h2019-20=∏i<jhi-hji-j(*)
szorzatot. Bebizonyítjuk, hogy e szorzat mindig +1-et ad értékül. Kezdjük annak megállapításával, hogy a rendezett kockához tartozó szorzat értéke nyilvánvalóan +1. Legyen most k<l. Ekkor hk és hl értékének kicserélése után a (*) szorzat értéke
(∏k<i<lhk-hihl-hi)⋅hk-hlhl-hk(∏k<i<lhi-hlhi-hk)=(-1)-szeresére
változik, tetszőleges hi értékekből való kiindulás után.
Egy 90∘-os forgatás végrehajtása után a hi értékek
hc1→hc2→hc3→hc4→hc1
és
he1→he2→he3→he4→he1
cseréje történik, ahol c1,c2,c3,c4 a forgatott C1,C2,C3,C4 csúcskockák sorszámát, e1,e2,e3,e4 pedig a forgatott E1,E2,E3,E4 élközépkockák sorszámát jelenti. Az ezáltal létrejövő változás, pontosabban mondva az, amit a változás a (*) szorzatban eredményez, megvalósítható a hc1↔hc2, hc1↔hc3, hc1↔hc4, he1↔he2, he1↔he3, he1↔he4, cserék egymás után történő elvégzése által, miközben a (*) szorzat értéke 6-szor vált előjelet, tehát végeredményben nem változik meg az előjele. Az már más kérdés, hogy a csúcskockák C1↔C2,C1↔C3 stb. cseréi külön-külön nem végezhetők el a bűvös kockán. Általánosan is igaz, és éppen a most bizonyított állításból következik, hogy semelyik két kis kockát nem lehet úgy kicserélni, hogy a többi kis kocka változatlan helyen maradjon. Ilyen csere esetén ugyanis a (*) szorzat értéke előjelt váltana.
A most mondott eredményeket összefoglalva s még a forgatások által megvalósítható változásokra vonatkozó állításokkal kiegészítve, a forgatások segítségével való rendezhetőség kérdését az alábbi 5 pontban összegezhetjük: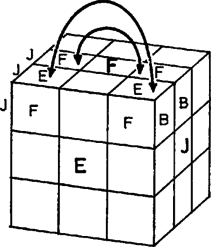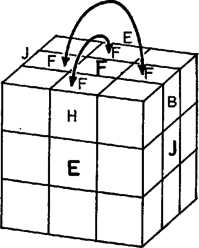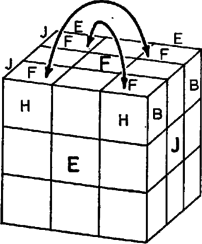
 

 
2A. ábra
 

 
2 B. ábra
 

 
2 C. ábra

 
1. Nem lehet forgatások segítségével a bűvös kockán olyan állapotváltozást létrehozni, amelynek során végeredményben egyetlen egy csúcskocka vagy élközépkocka helyben elfordul, az összes többi kis kocka pedig változatlan helyen és állásban marad.
2. Nem lehet sem két csúcskocka, sem pedig két élközépkocka helycseréjét elérni forgatások által, feltéve, hogy az összes többi kis kocka ‐ mindegy, hogy eredeti vagy elfordult állásban ‐ a helyén marad.
3. Lehet forgatások által két csúcskockát úgy kicserélni, hogy egyidejűleg két élközépkocka vagy másik két csúcskocka is helyet cserél. Lehet továbbá forgatások által két élközépkockát úgy kicserélni, hogy egyidejűleg két csúcskocka vagy másik két élközépkocka is helyet cserél.
Bizonyításként hajtsuk végre az alábbi forgatássorozatokat, mindig az alaphelyzetből kiindulva.
 

J1,F3,H1,F3,B1,E1,J1,H1,F1,H3,F1,J3,E3,B3,F3,H3,J3,E3,F2,H1,F3,E1,F1,H3,F2(l. 2. A ábra),J1,B1,F2,J3,B3,E3,H3,F2,E1,H1,(l. 2. B ábra).
 

Az előző sorozat után még F2(l. 2. C ábra).
 

4. Bármely 2 csúcskockát vagy bármely 2 élközépkockát el lehet forgatni helyben egyszerre, miközben az összes többi kis kocka változatlan helyen és állásban marad. Két csúcskocka azonban csak egymással ellentétes irányban forgatható el.
5. Bármely 3 csúcskockát vagy bármely 3 élközépkockát ki lehet cserélni úgy, hogy az összes többi kis kocka változatlan helyen és állásban marad.
A 4. és 5. pontnak az élközépkockára vonatkozó részét az első részben felsorolt elemi forgatássorozatok létezése bizonyítja. A csúcskockákra vonatkozó rész szintén elemi sorozatok megadásával bizonyítható. Itt most helyszűke miatt csak még 2 sorozatot mutatunk be: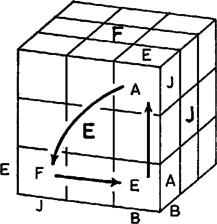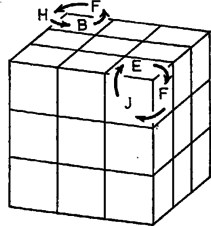
 
J1,F1,B3,F3,J3,F1,B1,F3(l. 2. D ábra)H1,J3,A2,J1,H3,F2  kétszer elvégezve(l. 2. E ábra)
 

 

 
2D.. ábra
 

 
2E. ábra

 

A 4. pont kiegészítő részének bizonyítása: ha két csúcskockát azonos irányban is el lehetne forgatni, akkor két ilyen csúcskockát először azonos irányban, majd folytatólag ellentétes irányban elforgatva, a végeredmény egyetlen csúcskocka helyben forgása lenne, amiről pedig már tudjuk, hogy lehetetlen.
Most gondolatban szedjük ki a bűvös kocka csúcskockáit és élközépkockáit; ezután 1 csúcskocka és 2 élközépkocka helyét üresen hagyva, rakjunk vissza 17 kis kockát a többi helyre. Számítsuk ki, hogy ez hányféleképpen tehető meg.
Az első csúcsba 8 csúcskocka bármelyikét 3-3 különböző módon helyezhetjük vissza; ez 24 különböző lehetőség. A következő csúcs kitöltéséhez már csak 7 csúcskocka közül választhatunk, ami 3⋅7=21 lehetőséget jelent. Ebből az indulásból már látható, hogy a 7 adott csúcs kitöltése összesen
24⋅21⋅18⋅15⋅12⋅9⋅6=37⋅8!=88179840
különböző módon történhet. Hasonlóan adódik, hogy 10 élközépkocka helyének kitöltése
24⋅22⋅20⋅18⋅16⋅14⋅12⋅10⋅8⋅6=29⋅12!=245248819200
különböző módon történhet. 7 csúcs kocka és 10 élközépkocka helyének a kitöltése tehát
37⋅8!⋅29⋅12!=21626001637244928000
különböző módon lehetséges. A két kimaradt élközépkocka visszarakásának helyét már egyértelműen meghatározza az a követelmény, hogy a (*) szorzat értéke +1 legyen. Valamelyik kimaradt élközépkockát kétféle állásban helyezhetjük el a megfelelő helyre. Végül az utolsó csúcskocka és az utolsó élközépkocka állását már egyértelműen meghatározza a fentiekben megvizsgált összegek 3-mal, ill. 2-vel való oszthatóságának a követelménye. Ugyanakkor a 3., 4. és 5. pontok állításából következik, hogy csak 7 csúcskocka és 10 élközépkocka helyével és állásával törődve, ezek együttese bármely 7 csúcskocka és 10 élközépkocka helyére, bárhogy áthelyezhető forgatások útján. Mindebből következik, hogy a bűvös kockának
37⋅8!⋅210⋅12!=43252003274489856000≈43⋅1018
egymástól különböző állása hozható létre a lapok forgatásai által. (Gondoljunk még az I. részben a 12.B ábrához tartozó sorozatok létezésére, a bizonyítás teljessé formálásához.)
A különböző lehetséges állások nagyságrendjének szemléltetése céljából először összehasonlításul megemlítjük, hogy egy lottószelvény különböző szabályos kitöltéseinek a száma ,,csak'' 43949268, tehát több nagyságrenddel kisebb. Hasonló nagyságrendű számokat pl. fizikai vagy kémiai táblázatokban találhatunk. (Avogadro-féle szám, Loschmidt-féle szám stb.) Ebből az észrevételből kiindulva kiszámítható, hogy nagyjából annyi különböző állás tekerhető ki a bűvös kockán, ahány molekulát számlálhatnánk meg egy normál állapotú ideális gáz 1,6cm3 térfogatában.
 

Feladatok
 

1. Képzeljünk el egy olyan különleges bűvös kockát, amelynek 3 lapját véletlenül egyforma színűre festették, másik 3 lapja azonban ezektől is, és egymástól is eltérő színű. Lehet-e egy ilyen kockán
a) egy kis kockát helyben elforgatni,
b) két kis kockát kicserélni,
feltéve, hogy a többi kis kocka változatlan helyen és állásban marad ?
2. Tekintsünk egy rendezetlen állású bűvös kockát. Soroljuk fel ‐ egymás alá írva ‐ a csúcskockákat és az élközépkockákat azonosító betűkombinációkat, s mindegyik után tegyünk egy jobbra mutató nyilat. Írjuk a nyíl hegyéhez annak a kis kockának a betűkombinációját, amelynek helyét a nyíl előtti kis kocka elfoglalja. Ha ezt minden egyes kis kockára megtettük, akkor ezután csoportosítsuk a kis kockákat a nyíl reláció tranzitív kiterjesztése alapján, vagyis két kis kocka kerüljön azonos csoportba, ha nyíl köti össze őket, de kerüljön különböző csoportba, ha sem közvetlenül, sem többszörös láncon keresztül nincsenek nyíllal vagy nyilakkal kapcsolva egymáshoz. Mutassuk meg, hogy az így kialakuló csoportok közül a páros elemszámú csoportok száma mindig páros ‐ feltéve, hogy az adott állás forgatások által jött létre a rendezett állásból.
3. Tekerjük ki lehetőleg kevés forgatással a rendezett bűvös kockából a 3. ábra szerinti, 12 darab L alakot tartalmazó állást.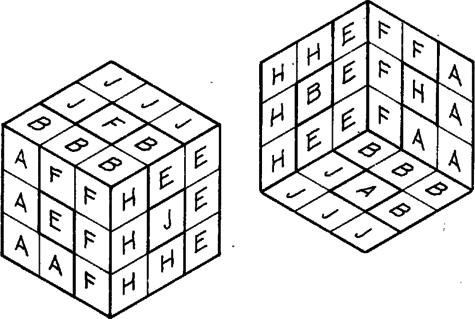
 

 
3. ábra

 
4. Mutassuk meg, hogy a bűvös kockának van olyan állása, amely nem rendezhető 15 vagy ennél kevesebb forgatással.
5. Bizonyítsuk be, hogy az alapállásból legfeljebb k forgatással előállítható, egymástól különböző állások száma kisebb vagy egyenlő mint az
sk=90+1154116(6+54)k+90+1154116(6+54)k-1629
kifejezés értéke. (k tetszőleges nemnegatív egész szám.)
Írjuk fel az
sk<S,ill.azsk>S
egyenlőtlenség nemnegatív egész megoldásait, ha
S=43252003274489856000.
 

Irodalom
 


[1] D. Singmaster: Notes on the 'Magic Cube' (Polytechnic of the South Bank, London, 1979).

[2		] E. R. Berlekamp, J. H. Conway és R. K. Guy: Winning Ways (részlet), kézirat (Cambridge 1979).

[3		] J. H. Conway és munkatársai: Jegyzetek a bűvös kockáról, kézirat (Cambridge, 1979).

[4		] Fercsik János és Karsai Zsuzsanna: Az algoritmizálás, kézirat (Dunaújváros, 1979).

[5		] Perjés Zoltán: On Rubik's cube, kézirat (MTA KFKI, Budapest, 1979).