|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Képzelje el az olvasó, hogy az asztalon egy halom, külsőre teljesen egyforma pénzdarab van. Valaki elárulta, hogy az egyik érme hamis, de ez a valódi érméktől csak súlyban tér el. Még azt se tudjuk, hogy a hamis érme könnyebb-e vagy éppen nehezebb a többinél. Rendelkezésünkre áll egy egyenlő karú mérleg, súlyok nélkül. Hogyan használjuk a mérleget, ha minimális számú méréssel szeretnénk a hamis érmét kiválasztani, és azt is meg akarjuk közben tudni, hogy az nehezebb-e vagy sem a többinél?
Olvasóink közül bizonyára sokan megoldották ezt a feladatot érmére. Az 1. ábrán egy lehetséges megoldás látható. Az első mérés három kimenetének megfelelően a második méréshez három különböző módon osztjuk szét az érméket. A bal oldali nyíl annak az esetnek felel meg, amikor a bal oldali serpenyő süllyed le, a középső nyíl az egyensúlynak, a jobb oldali pedig annak az esetnek, amikor a jobb oldali serpenyő a nehezebb. Hasonló módon ábrázoltuk a harmadik mérésre vonatkozó kilenc felosztást. (Az ábrán az érméket megszámoztuk, a és betűk azt jelzik, hogy a hamis érme könnyebb vagy nehezebb a többinél.) Ennek a megoldásnak jellemző tulajdonsága, hogy a soron következő méréshez az érmék felosztása függ az előző mérés eredményétől.
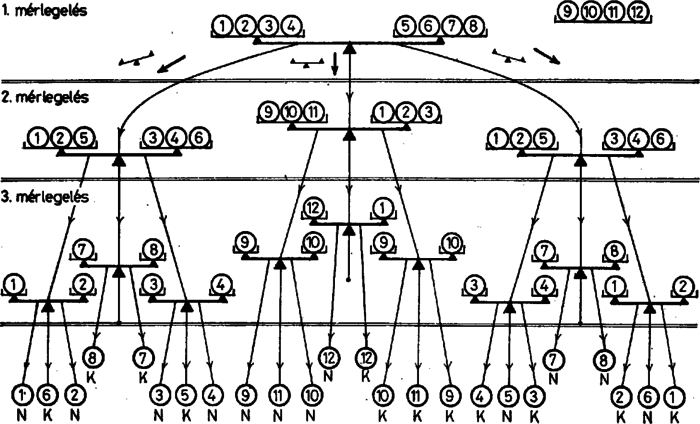 1. ábra
Most a feladatot általános formában mondjuk ki:
Adott , külsőre teljesen egyforma érme. Mindegyik érme, egy kivételével, ugyanolyan súlyú, arról az egyről, amelyik súlyban különbözik a többitől, nem ismert, hogy súlya melyik irányban tér el. Legkevesebb hány méréssel lehet egy egyenlő karú mérleggel ezt az érmét megtalálni és megállapítani a típusát?
Ez a feladat több mint évvel ezelőtt sok, főleg angol és amerikai matematikus figyelmét vonta magára. -ben a ,,The matematical Gazette'' című angol folyóiratban megjelent a feladatnak egy megoldása. Szerzője R. L. Goodstein, aki később a matematikai logika ismert szakemberévé vált.
Goodstein módszert adott a hamis érmének és típusának meghatározására méréssel, ha az érmék száma . (Vegyük észre, hogy -ra .) Azonban kiderült, hogy -ra eredménye nem a lehető legjobb: méréssel érméből is ki lehet választani a hamisat, és meg lehet határozni a típusát. Ezt egymástól függetlenül több matematikus is megtalálta, és -ban ugyanez a folyóirat egy meglehetősen hosszú listában közölte a megoldók nevét és a különböző eredményeket, melyeket a hamis érmék utáni nyomozás terén értek el. Ugyanebben a számban jelent meg a lehető legjobb megoldás, F. J. Dyson tollából, akiből később ismert elméleti fizikus lett.
Dyson ötlete a hármas számrendszer felhasználásán alapszik. Minden érmét egy ügyesen megválasztott hármas számrendszerbeli számmal jelöl meg, és ezzel egy csapásra lehetővé teszi a méréssorozat tervezését és kiértékelését. Ennek a megoldásnak különös szépsége abban rejlik, hogy a soron következő méréshez kiválasztott érmék nem függnek az előző mérések eredményétől.
Az elmúlt pár évben ennek a feladatnak több új megoldása is megjelent, de közben Dyson módszerét érdemtelenül elfeledték. Ezért érdemes erről részletesebben szólnunk. Dyson megoldását két lépésben ismertetjük, először az esetet, majd az esetet vizsgálva.
Első rész. Legyen az érmék száma . Tekintsük az összes jegyű (, és számjegyekből álló) triadikus számokat: , , . Ezek száma . Ezeket használjuk fel az érmék megjelölésére a következő módon. Minden számot felhasználunk jelként, kivéve azt a hármat, amelyik csupa egyforma számjegyből áll: , , .
A jeleket párokba állítjuk: egy pár két komplementer jelből áll, azaz azokból, amelyekben a sorrendben megfelelő számjegyek összege (más szavakkal komplementer jelek azok, amelyek összege .
Egy jelet jobb oldalinak nevezünk, ha benne a balról számított első két nem egyforma jegy, , vagy . Ellenkező esetben a jelet bal oldalinak nevezzük. Világos, hogy minden, komplementer jelekből álló pár egyik eleme jobb oldali, a másik bal oldali.
Vegyük észre, hogy a jelpárok száma éppen megegyezik az érmék számával. Számozzuk meg az érméket -től -ig, és feleltessünk meg minden érmének egy jelpárt. Például érmét a táblázatban látható módon lehet ,,megjelölni''.
Legyen , , illetve mindazoknak az érméknek a halmaza, amelyek jobb oldali jelében az -edik helyen , , illetve áll. Könnyű belátni, hogy az , és halmazokban egyforma sok elem van, és hogy a halmazoknak nincs közös elemük (lásd például az 1. táblázatot). Ezek után az érméket ‐ Dyson szerint ‐ a következőképpen kell mérnünk. Összesen egymást követő mérést végzünk. Az -edik méréshez a bal oldali serpenyőbe tesszük az halmazban levő érméket, a jobb oldali serpenyőbe pedig az halmazbeli érméket. Egy mérés eredményét -val jelöljük, ha a bal oldali serpenyő a súlyosabb, -gyel, ha a serpenyők egyenlő súlyúak, és -vel, ha a jobb oldali serpenyő a nehezebb (lásd a 2. ábrát). Az -edik mérés eredményét -vel jelöljük. A számjegyekből elkészítjük , jelet.
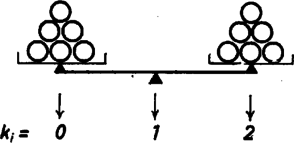 2. ábra
Állítjuk, hogy a hamis érme jele, mégpedig, ha jobb oldali jel, akkor könnyebb a többinél, és ha bal oldali jel, akkor nehezebb a többi érménél. Valóban, nézzük, mi történik, amikor végrehajtjuk az -edik mérést. A mérés eredményeképpen a serpenyők vagy egyensúlyban vannak, vagy valamelyik nehezebb.
Ha a serpenyők egyensúlyban vannak, a hamis érme egyikben sincs, következésképpen az halmazban van. De ebből következik, hogy a bal oldali (és a jobb oldali) jelében az -edik helyen áll, amit a mérés eredménye, is mutat.
Ha valamelyik serpenyő lesüllyed, a hamis érme az egyik serpenyőben van. Tegyük fel például, hogy, a jobb oldali serpenyő a nehezebb, azaz . Ez az eredmény kétféleképpen következhet be:
‐ a hamis érme a jobb oldali serpenyőben van (és ekkor nehezebb a többinél), azaz az halmazba esik, a jobb oldali jelében az -edik helyen -es áll. Tehát a mérés eredménye megegyezik a jobb oldali jelének -edik jegyével;
‐ a hamis érme a bal oldali serpenyőben van, és ekkor könnyebb a többinél, azaz az halmazba esik. Tehát a jobb oldali jelének -edik jegye , és a mérés eredménye megegyezik a bal oldali jelének -edik jegyével.
Teljesen hasonló a ,,szimmetrikus'' eset, amikor a bal oldali serpenyő a nehezebb .
Így valóban a méréssorozat eredményéből adódó jel a hamis érme jele, éspedig nehezebb érme esetén a jobb oldali, könnyebb érme esetén a bal oldali jel, amit bizonyítanunk kellett.
Érdemes megjegyezni, hogy a hamis érme típusát rendszerint az összes mérés elvégzése előtt megkapjuk ‐ amint a jel összeállításában két különböző számjegyet kapunk.
A leírt módszer fontos jellemzője ‐ ahogyan azt korábban már említettük ‐, az a körülmény, hogy a mérésekhez kiválasztott érmék nem függenek a megelőző mérések eredményétől. Például érme esetén, melyeket a táblázatnak megfelelően jelöltünk meg, elegendő a következő három mérést elvégezni: , , .
Második rész. Röviden vázoljuk Dyson módszerét az esetre. Ha ebben az esetben az érmékhez megfelelő módon tudunk jeleket rendelni, akkor az és halmazokban egyforma sok érmének kell lennie. Ezért a következőket tesszük. Osszuk a jeleket hatos csoportokba: egy csoportba azok a jobb oldali jelek tartozzanak, amelyek egymásból a jelek ciklikus cseréjével , , kaphatók, a baloldali párjukkal együtt.
Minden csoportba három jobb oldali és három baloldali jel tartozik. Azt a csoportot, amely a , és a jobb oldali jeleket tartalmazza, különlegesen kezeljük. Osszuk az érméket hármas csoportokba mindaddig, amíg ez lehetséges, és adjunk nekik jeleket a következő módon. Egy csoportba tartozó érméknek egy csoportba tartozó jelpárokat adjunk, a maradéknak pedig ‐ ha egyáltalán volt ‐ a különleges csoportból rendeljünk jelpárokat. Ha egy érme maradt ki, akkor az jobb oldali jelet kapja, ha kettő, akkor a és a jobb oldali jeleket kapják (és a megfelelő bal oldaliakat is).
Ezekkel a jelekkel az első mérés a régi módszer szerint végezhető. Azt, hogy az utolsó mérés mi legyen, mindenki önállóan kigondolhatja.
Ezzel Dyson módszerét leírtuk. Most megmutatjuk, hogy ez, meghatározott értelemben, a lehető legjobb. Pontosabban szólva megmutatjuk, hogy ha érme közül méréssel ki tudjuk választani a hamisat, és meg tudjuk mondani a típusát, akkor (Természetesen nem vesszük figyelembe a ,,szerencsés'' eseteket: tetszőleges számú érme közül már két méréssel megkaphatjuk a hamisat.)
Számozzuk meg az érméket az -től -ig terjedő számokkal, és készítsünk elő papírlapot. Írjuk ezekre az összes lehetséges esetet: az egyes érme könnyebb, az egyes érme nehezebb, a kettes érme könnyebb stb. Világos, hogy ehhez mind a papírlapot felhasználtuk, és egyetlen eset sem maradt ki. Jelöljük, ahogyan azt korábban tettük, egy mérés eredményét a , vagy számjeggyel. Mindegyik mérés azt adja meg, hogy az elképzelhető esetek egyik része nem jöhet elő, míg másik része továbbra is gyanús marad. Nézzük az első mérést. Anélkül, hogy azt valóban végrehajtanánk, írjuk mindegyik lapra az első mérés végeredményét, feltéve, hogy a papírlapon áll a gyanúsított. Világos, hogy minden papírlapra a , , számjegyek közül pontosan az egyik kerül. Ily módon a papírlapokat három csoportra osztottuk. Tehát a legnagyobb elemszámú csoportban legalább lap van. Következésképp bárhogy is szerveztük meg az első mérést, előfordulhat, hogy utána még legalább lap tartalmaz gyanúsítható esetet.
Hasonló módon a második mérés a gyanúsítottaknak ezt a csoportját három részcsoportra osztja. Ezért közülük a legnagyobb elemszámú legalább lapot tartalmaz. Pontosan ugyanígy, mérés után gyanús papírlapot kaphatunk az egyik csoportban. Tehát ha , akkor a hamis érmét és típusát általában méréssel nem lehet megállapítani. Ezért ha mérés elegendő, akkor .
De ezzel még nem vagyunk készen! Még nem vizsgáltuk meg a esetet ( páros szám, tehát nem egyenlő sem -vel, sem -nel). Erre a fönti meggondolás nem elegendő. Fordítsunk egy kicsit több figyelmet az első mérésre. Világos, hogy ugyanannyi papírlapra kerül a számjegy, mint ahányra a számjegy. Legyen ezek száma külön-külön , ebből adódik, hogy lapra kerül -es.
Figyeljük meg, hogy páros szám. Valóban, ha a bal és jobb oldali serpenyőbe is érme került, akkor . Ha akár , akár nagyobb, mint , akkor a keresett papírlap meghatározásához a megmaradt mérés nem feltétlenül lesz elegendő. Ha pedig és , akkor, mivel páratlan, , és . Tehát , így ha mérés elegendő, akkor .
Nyilvánvaló, hogy az értékekre a feladat nem megoldható, hiszen -re az érme hamis, de ismeretlen típusú; -re az érmék különböző súlyúak, és közülük a hamisat lehetetlen ilyen méréssel kiválasztani.Bizonyítsuk be, hogy ez valóban jel, azaz nem mind egyforma. |
 PDF | MathML
PDF | MathML