Kezdőlap


Cím:	Az 1979. évi (11.) Nemzetközi Fizikai Diákolimpia feladatai
Füzet:	1979/november, 161 - 165. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Egy $m = 12 t$ tömegű űrhajó $h = 100 km$ magasságban körpályán kering a Hold körül. Abból a célból, hogy elérje a Holdat, a hajtóművet rövid időre bekapcsolják az $X$ pontban. A rakétából kiáramló gázok sebessége a rakétához képest $u = 10 000 m/s$ . A Hold sugara $R = 1700 km$ , felszínén a szabadesés gyorsulása $g = 1, 7 {m/s}^{2}$ . Az űrhajó a megközelítést kétféleképp hajthatja végre (1. ábra), és az a kérdés, hogy a két esetben mennyi üzemanyagot fogyaszt? $a)$ A Holdat az $X$ ponttal ellentétes $A$ pontbon éri el. $b)$ Az $X$ pontban a Hold középpontja felé adott impulzussal elérik azt, hogy az űrhajó $B$ -ben érintőlegesen éri el a Hold felszínét.

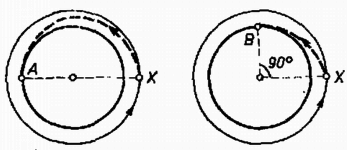1. ábra

Megoldás. A nehézségi gyorsulás a Hold felszínén

g = f M / R^{2}

(

f

a tömegvonzási állandó,

M

a Hold tömege). A körpályán keringő űrhajó eredeti sebessége

v_{0}

, erre nézve

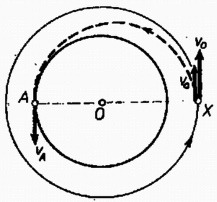\begin{matrix} \frac{v_{0}^{2}}{R + h} = \frac{f M}{{(R + h)}^{2}} = \frac{g R^{2}}{{(R + h)}^{2}}, v_{0} = \sqrt[]{\frac{g R^{2}}{R + h}} = 1652 m/s . \end{matrix}

2. ábra

a) Az űrhajó a rakéta ellenirányú működtetésével sebességét

v_{0}

-ról egy bizonyos

v_{a}

-ra csökkenti. Ezután ellipszispályán kering; az ellipszis nagytengelyének végpontjai

A

és

X

(2. ábra). A sebesség

A

-ban

v_{A}

X

-ben

v_{a}

. A területi sebesség állandósága (Kepler II. törvénye) szerint:

\begin{matrix} v_{A} R = v_{a} (R + h), v_{A} = \frac{R + h}{R} \cdot v_{a}; \end{matrix}

A sebesség

v_{a}

-ról

v_{A}

-ra növekszik, a mozgási energia gyarapodását a gravitációs energia csökkenése fedezi:

\begin{matrix} \frac{m v_{A}^{2}}{2} - \frac{m v_{a}^{2}}{2} = \frac{f m M}{R} - \frac{f m M}{R + h}, \end{matrix}

ebből:

\begin{matrix} v_{A}^{2} - v_{a}^{2} = 2 f M \cdot \frac{h}{R (R + h)} = \frac{2 g h R}{R + h} = 0, 321 \cdot 10^{6} {(m/s)}^{2} . \end{matrix}

Az impulzustörvényből származtatva

v_{A}

értéket felhasználva

\begin{matrix} v_{a}^{2} [{(\frac{R + h}{R})}^{2} - 1] = v_{a}^{2} \cdot \frac{h (2 R + h)}{R^{2}} = \frac{2 g h R}{R + h}, \\ v_{a}^{2} = \frac{2 g R^{3}}{(R + h) (2 R + h)} = 2, 65 \cdot 10^{6} {(m/s)}^{2}, \\ v_{a} = 1628 m/s, v_{A} = 1724 m/s . \end{matrix}

Az ellenrakétázással létrehozandó sebességváltoztatás:

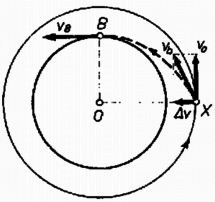\begin{matrix} Δ v = v_{0} - v_{a} = 24 m/s . \end{matrix}

3. ábra

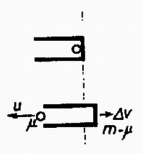4. ábra

Az üzemanyag mennyiségének meghatározása céljából az impulzustörvényt az űrhajóhoz rögzített koordináta-rendszerben alkalmazzuk (4. ábra). A kidobott anyagmennyiség:

μ = \frac{m Δ v}{u + Δ v} = 28, 7 kg

.
(L. az 1969. évi Eötvös-verseny 1. feladatát, ahol hasonló kérdés kissé eltérő, érdekes megoldása található.)
b) A rakétával a sugár mentén kifelé tüzelnek, és ezzel

Δ v

sebességet adnak hozzá a meglevő

v_{0}

-hoz, a középpont felé irányítva (3. ábra). Ekkor az űrhajó sebessége

v_{b} = \sqrt[]{v_{0}^{2} + Δ v^{2}}

, amellyel olyan ellipszis (parabola, hiperbola) pályán indul el, amelynek csúcspontja

B

, fókusza továbbra is

O

, és

X

-ben a pálya érintője

v_{b}

O X

a kúpszelet ún. paramétere.

B

-ben a sebesség a

v_{b}

-nél nagyobb

v_{B}

lesz.
A területi sebesség állandóságát írjuk fel, figyelembe véve, hogy

X

-nél a sugárra merőleges

v_{0}

összetevő használandó:

\begin{matrix} v_{B} R = v_{0} (R + h), v_{B} = \frac{R + h}{R} \cdot v_{0} = 1749 m/s . \end{matrix}

A sebesség

v_{b}

-ről

v_{B}

-re növekszik, a mozgási energia növekedését a gravitációs energia csökkenése fedezi:

\begin{matrix} \frac{m v_{B}^{2}}{2} - \frac{m v_{b}^{2}}{2} = \frac{f m M}{R} - \frac{f m M}{R + h} = f m M \cdot \frac{h}{R (R + h)}, \end{matrix}

átalakítva:

\begin{matrix} v_{B}^{2} - (v_{0}^{2} + Δ v^{2}) = \frac{2 g h R}{R + h}, \\ Δ v^{2} = v_{B}^{2} - v_{0}^{2} - \frac{2 g h R}{R + h} = v_{0}^{2} {(\frac{R + h}{R})}^{2} - v_{0}^{2} - \frac{2 g h R}{R + h} = \\ = v_{0}^{2} {(\frac{R + h}{R})}^{2} - v_{0}^{2} - \frac{2 h}{R} \cdot v_{0}^{2} = v_{0}^{2} \cdot \frac{h^{2}}{R^{2}}, \\ Δ v = \frac{h}{R} \cdot v_{0} = 97 m/s . \end{matrix}

Ismét alkalmazzuk az űrhajóra az impulzustételt:

\begin{matrix} Δ v (m - μ) = μ u, μ = \frac{m Δ v}{u + Δ v} = 115 kg . \end{matrix}

Az űrhajó indulási sebessége az új pályán

v_{b} = 1655 m/s

. Az űrhajó az

X

pontból a kör érintőjéhez képest

arc tg (Δ v / v) = 3^{\circ} 21'

-es szögben indul el. A

B

pontban a körpályán való mozgáshoz szükséges sebesség

\sqrt[]{g R} = 1700 m/s

. Mindaddig ellipszispályán mozog, amíg

v_{B}

kisebb

\sqrt[]{2} \cdot 1700 = 2404 m/s

-nál. A mi

1749 m/s

sebességünk messze ez alatt marad, tehát a pálya ellipszis.

2. Egy alumíniumdarab tömegét sárgaréz súlyokkal mérjük, először száraz, majd

15, 2 Hgmm

parciális vízgőz-nyomású nedves levegőben. A teljes nyomás

(760 Hgmm)

és a hőmérséklet

(20^{\circ} C)

mindkét esetben ugyanaz. Legalább mekkora tömegű alumíniumdarab esetében veszünk észre különbséget a két mérés között, ha a mérleg érzékenysége

0, 1 mg

? Az alumínium sűrűsége

2, 7 {g/cm}^{3}

, a sárgarézé

8, 5 {g/cm}^{3}

Megoldás. A vízgőz parciális nyomása a teljes nyomás ötvened része, tehát a levegő térfogatának ötvened része van vízgőzzel helyettesítve.

20^{\circ} C

-on a levegő sűrűsége

0, 0012 {g/cm}^{3}

, a vízgőzé

0, 00075 {g/cm}^{3}

, a nedves levegőnké:

\begin{matrix} \frac{49 \cdot 0, 0012 + 1 \cdot 0, 00075}{50} {g/cm}^{3} = 0, 00119 {g/cm}^{3} . \end{matrix}

A száraz és nedves levegő sűrűségének különbsége így

0, 00001 {g/cm}^{3}

1

gramm alumínium térfogata

0, 370 {cm}^{3}

1

gramm sárgarézé

0, 117 {cm}^{3}

, ezek különbsége

0, 253 {cm}^{3}

. A száraz levegőt nedvessel felcserélve

1

grammos testek kiegyensúlyozásakor a felhajtóerők különbsége

0, 253 {cm}^{3} \cdot 0, 00001 {g/cm}^{3} = 0, 0000025

grammos tömeg súlyát jelenti. Mérlegünk

0, 0001

grammos tömeg súlyát képes érzékelni, ezért az eltérés akkor válik észrevehetővé, ha a mérendő alumíniumdarab tömege az

1 g

-os mintáénál

0, 0001 g : 0, 0000025 g = 40

-szer nagyobb.

3. A Hold felszínére egy

λ = 0, 69 μ m

hullámhosszú fényt adó lézer sugarát irányítjuk egy

D = 2, 6 m

átmérőjü parabolatükrös távcső segítségével. A Holdon

d = 20 cm

átmérőjű síktükröt helyeztek el a fény visszaverése céljából. Ez a tükör a fényt pontosan a földi távcső felé veri vissza; a távcső fókuszában fotoérzékelő van. A Föld‐Hold távolság

L = 380 000 km

. a) Milyen szögpontossággal kell beállítani a távcsövet? b) Az eredetileg kibocsátott energiából mennyit fog fel a fotoérzékelő? (A veszteségektől eltekintünk.) c) Ha a fénylökés energiája

1 joule

, akkor szabad szemmel megfigyelve hány foton jutna szemünkbe? A pupilla átmérője

5 mm

. d) Mennyi energiát kapna vissza a fotoérzékelő, ha a Holdon nem helyeztünk volna el tükröt? A Hold felszíne a ráeső fény

10 %

-át minden irányban egyenletesen veri vissza.

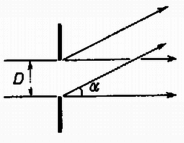5. ábra

Megoldás. a) A lézer csak mint erős, pontszerű fényforrás szerepel, a mi esetünkben az irányításban nincs szerepe. A távcső

π {(D / 2)}^{2} = 5, 31 m^{2}

nagyságú nyílásterülete mint fényt kibocsátó rés szerepel, és a sugárnyalábot a diffrakció szélesíti ki (5. ábra). A rés Huygens szerint mint hullámfelület működik, az eredeti irányban adja a legnagyobb intenzitást és

λ = D sin α

irányban az első interferenciás kioltást. Legjobb volna, ha a tengely pontosan a holdi tükör felé mutatna. Ha

sin α = λ / D

szögnél nagyobb az irányeltérés, akkor biztosan alig kap fényt a holdi tükör. Ez a szög:

α \approx sin α = \frac{λ}{D} = \frac{0, 69 \cdot 10^{- 6} m}{2, 6 m} = 2, 65 \cdot 10^{- 7} = 0, 055''

. Ennél lényegesen pontosabb legyen az irányítás. E szögön belül sem egyenletes a fényeloszlás, a széle felé csökken, ezért minden további számításunk csak közelítő pontosságú.
b) Az ismertetett diffrakció következtében a Holdon egy megvilágított kör keletkezik, amelynek átmérője

α L = \frac{λ}{D} \cdot L = 101 m

, területe

π {(L λ / 2 D)}^{2} = 7987 m^{2}

. Ezen oszlik szét az

E

összes kisugárzott energia és így az átlagos energiasűrűség:

\begin{matrix} E : \frac{π λ^{2} L^{2}}{4 D^{2}} = \frac{4 D^{2} E}{π λ^{2} L^{2}} = 0, 125 \cdot 10^{- 3} \frac{1}{m^{2}} E . \end{matrix}

d

átmérőjű és

π {(d / 2)}^{2} = 0, 0314 m^{2}

területű holdi síktükörre jutó energia:

\begin{matrix} \frac{4 D^{2} E}{π λ^{2} L^{2}} \cdot π {(\frac{d}{2})}^{2} = {(\frac{D d}{L λ})}^{2} \cdot E = 3, 94 \cdot 10^{- 6} E . \end{matrix}

A síktükör mindezt az energiát visszadobja, de ismét a diffrakció miatt

λ / d = β = 3, 45 \cdot 10^{- 6} radián = 0, 71''

nagyságú szögtartományban (6. ábra, nem méretarányos). A Földön

β L = \frac{λ L}{d} = 1310 m

átmérőjű,

1, 72 \cdot 10^{6} m^{2}

területű kör kap fényt. Ezen oszlik szét a Hold által visszavert

{(D d / L λ)}^{2} E

energia, tehát a visszavert fény által a Földön létrehozott energiasűrűség:

\begin{matrix} {(\frac{D d}{L λ})}^{2} E : π {(\frac{L λ}{2 d})}^{2} = \frac{4 D^{2} d^{4}}{π L^{4} λ^{4}} \cdot E = 2, 3 \cdot 10^{- 12} \frac{1}{m^{2}} E . \end{matrix}

π {(D / 2)}^{2}

területű észlelő távcsőbe jutó energia:

\begin{matrix} \frac{4 D^{2} d^{4} E}{π L^{4} λ^{4}} \cdot π {(\frac{D}{2})}^{2} = {(\frac{D d}{L λ})}^{4} E = 15, 8 \cdot 10^{- 12} E . \end{matrix}

Tehát az eredeti energia

16

billiomod részét kapjuk vissza.
c) A pupilla területe

π \cdot 2, 5^{2} {mm}^{2} = 20 {mm}^{2} = 20 \cdot 10^{- 6} m^{2}

; ezt kell szorozni a Földön létrejött

2, 3 \cdot 10^{- 12} \frac{1}{m^{2}} \cdot E

energiasűrűséggel

(E = 1 joule)

, az energia

46 \cdot 10^{- 18} joule

.
A piros fényünk rezgésszáma

f = (3 \cdot 10^{8} m/s) : (0, 69 \cdot 10^{- 6} m) = 4, 35 \cdot 10^{14} s^{- 1}

, fotonjának energiája:

h f = 2, 89 \cdot 10^{- 19} joule

. A szembe jutó fotonok darabszáma

46 \cdot 10^{- 18} : 2, 89 \cdot 10^{- 19} = 155

foton.
Vajon észrevehetnénk-e szabad szemmel a visszavert fényt? Szemünk ideghártyájában csak a pálcikák fokozott érzékenységének vehetnénk hasznát. Ezek a

0, 51 μ m

hullámhosszú zöld fény iránt a legérzékenyebbek, ekkor alkalmas körülmények között néhány fotont is érzékelni lehet. A pálcikák érzékenysége

0, 6 μ m

-nél ennek százada, és még nagyobb hullámhosszú fény iránt teljesen érzéketlenek. Így szó sem lehet a szabad szemmel történő megfigyelésről. Azonkívül a Hold erős fénye is zavarna.

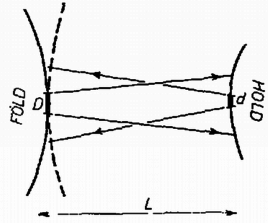6. ábra

d) Ha nem helyezünk a Holdra tükröt, akkor a Holdra érkező összes fény tizede,

0, 1 E

verődik vissza. (A

101

méteres kör teljes egésze könnyen ráfér a Holdra.) De a sokkal nagyobb,

0, 1 E

energia most

L

sugarú,

2 π L^{2} = 0, 907 \cdot 10^{18} m^{2}

területű félkörön oszlik szét, és így a Földön létrehozott energiasűrűség:

\begin{matrix} \frac{0, 1 E}{2 π L^{2}} = 1, 1 \cdot 10^{- 18} \frac{1}{m^{2}} \cdot E, \end{matrix}

ebből a távcső által felfogott energia:

\begin{matrix} π {(\frac{D}{2})}^{2} \cdot \frac{0, 1 E}{2 π L^{2}} = 5, 9 \cdot 10^{- 18} E . \end{matrix}

A b) esethez képest az energia-arány:

\begin{matrix} {(\frac{D d}{L λ})}^{4} \cdot E : [π {(\frac{D}{2})}^{2} \cdot \frac{0, 1 E}{2 π L^{2}}] = 80 \cdot \frac{D^{2} d^{4}}{L^{2} λ^{4}} = 27 \cdot 10^{6} . \end{matrix}

Az eredmény több milliószor rosszabb a holdi tükör nélkül.

Kísérleti feladat Egy négy kivezetéses ,,fekete doboz'' belsejét kellett mérésekkel felderíteni. Váltó- és egyenáramú áramforrások és mérőműszerek, valamint tolóellenállás adva voltak.

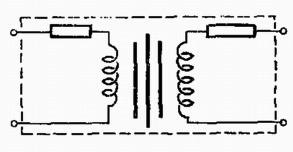7. ábra

A doboz belsejét a 7. ábra mutatja. A következő megállapításokra kerülhetett sor.
A dobozban nincs áramforrás (sehogyan sem jön ki belőle semmi).
A dobozban nincs egyenirányító (átsarkalásokkor nem változnak a mérési adatok).
A dobozban két, egyenáram szempontjából nem összefüggő alkatrész van.
Ezután mérhetők az ellenállások, induktivitások és a kölcsönös indukció együtthatója.