Kezdőlap


Cím:	1979. évi fizika OKTV feladatai
Füzet:	1979/október, 81 - 87. oldal	PDF \| MathML
Témakör(ök):	OKTV

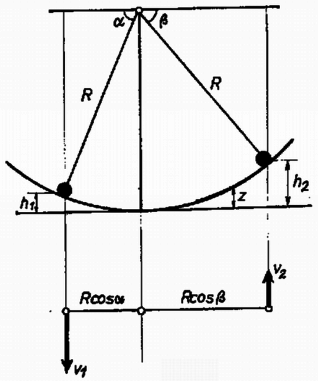
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az I. forduló feladatai

1. Vízszintes asztallapon

m

tömegű test nyugszik, amelyhez

D_{0}

rugóállandójú,

L

hosszúságú rugó van erősítve (1. ábra). A rugó tengelyének egyenesében

v_{0}

sebességgel egy ugyancsak

m

tömegű test érkezik és a rugónak ütközik. A súrlódás és a rugó tömege elhanyagolható.

1. ábra

a) Mennyi lesz a rugó legrövidebb hossza az ütközés folyamán?
b) Az érkező test rögzítődik a rugó bal végéhez. Mennyi a keletkező rezgés ideje?
Számadatok:

m = 1 kg

L = 0, 2 méter

D_{0} = 250 newton/méter

v_{0} = 0, 8 m/s

(Holics László)

2. ábra

Megoldás. A rugó akkor a legrövidebb, amikor a két test éppen egyenlő sebességgel mozog (2. ábra). Az impulzustörvény szerint ez a sebesség az eredetinek a fele. Ebben az állapotban a mozgási energia

0, 5 \cdot 2 m {(v_{0} / 2)}^{2} = m v_{0}^{2} / 4

, vagyis az eredetinek a fele. A másik feléből lett az összenyomott rugó

0, 5 D_{0} x^{2}

rugalmas energiája; ebből az összenyomódás

x

hossza:

x = v_{0} \sqrt[]{m / 2 D_{0}} = 3, 58

cm és a rugóhossz:

L - x = 16, 4

cm.
Összeakadás után a tömegek a

v_{0} / 2

sebességgel haladó súlypont körül rezegnek. Mindegyik tömeghez a súlyponttól mérve a rugóhossz fele tartozik, ezért a rezgésidőnek a

T = 2 π \sqrt[]{m / D}

képlet szerint történő kiszámításakor az előbbi rugóállandó kétszeresével,

D = 2 D_{0}

-al kell számolnunk:

\begin{matrix} T = 2 π \sqrt[]{m - / 2 D_{0}} = 0, 28 s . \end{matrix}

L = 0, 5 méter

hosszúságú, egyenként

m_{1} = 1 kg

tömegű rudakból csuklós szerkezetet állítunk össze, amelynek bal oldali vége a talajhoz, a jobb oldali vége az

m_{2} = 2 kg

tömegű testhez csuklósan van erősítve (3. ábra). A súrlódás elhanyagolható. Az

m_{2}

tömegű testet a rudak 60

^{\circ}

-os helyzetében elengedjük.
a) Mekkora sebességgel érkezik a talajhoz a szerkezet

A

-pontja?
b) Mekkora ebben a pillanatban az

m_{2}

tömegű test gyorsulása?
(Holics László)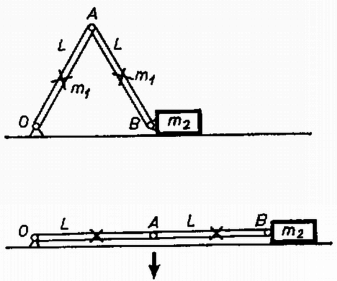

3. ábra

Megoldás. A leérkezés pillanatában az

m_{2}

tömegű test már áll. Így a helyzeti energia csökkenése egyenlő a rudak mozgási energiájával. A helyzeti energia csökkenése

2 m_{1} g L \sqrt[]{3} / 4

, a rudak mozgási energiája (ha

ω

szögsebességgel érik el a talajt)

2 \cdot (ω^{2} Θ / 2)

, ahol

Θ = m_{1} L^{2} / 3

a tehetetlenségi nyomaték. Tehát

\begin{matrix} \frac{ω^{2} m_{1} L^{2}}{3} = m_{1} g L \frac{\sqrt[]{3}}{2}, \end{matrix}

azaz

\begin{matrix} ω = \sqrt[]{\frac{3 \sqrt[]{3} g}{2 L}} = 3, 57 m/s . \end{matrix}

A

pontnak a leérkezés pillanatában csak centripetális gyorsulása van: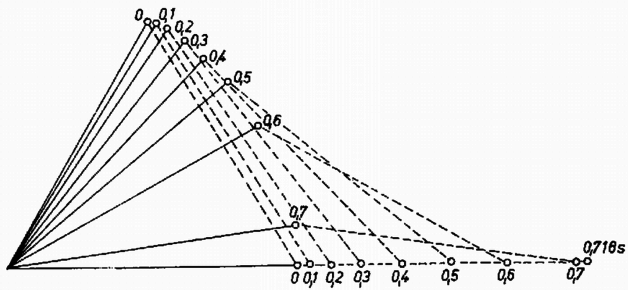

\begin{matrix} a = \frac{y^{2}}{L} = \frac{3 \sqrt[]{3}}{2} \cdot g, \end{matrix}

azonban a berendezés geometriájából következően a

B

pont gyorsulása ebben a pillanatban ennek kétszerese, így a kérdezett gyorsulás nagysága, amely szintén független a tömegektől és a rúdhossztól

\begin{matrix} 3 \sqrt[]{3} g = 50, 92 {m/s}^{2} . \end{matrix}

Amint az az ilyen feladatoknál megszokott, a sebességnek az úttól való függését az energiatétellel viszonylag könnyen meg lehet határozni. Azonban, ha a sebességnek az időtől való függését keressük, akkor a választ nem adhatjuk meg elemi függvényekkel zárt alakban, hanem numerikus módszerekkel kell dolgozni a szükséges pontosságig. Feladatunkban fokról fokra kiszámíthatjuk, mekkora a szögsebesség megváltozása, a szögsebességből viszont közelítően megtudjuk az egyes állapotok között eltelt időt. Így megszerkeszthető a mozgás időbeli lefolyásának képe (4. ábra). Félméteres rudak esetében

0, 72

s múlva lesz a mozgásnak vége. Ilyen táblázatból a sebességek és a gyorsulások időfüggése is meghatározható. Az

m_{2}

tömegű test sebessége közvetlenül a leérés előtt maximális, azután hirtelen esik nullára.

4. ábra

L = 1

méter hosszú,

γ

fajsúlyú vékony pálca egyik végét a víz alatt

h = 0, 8

méter mélységben csapágyaztuk (5. ábra). Határozzuk meg a pálca egyensúlyi helyzetét és vizsgáljuk meg az egyensúlyi helyzet stabilitását, ha a)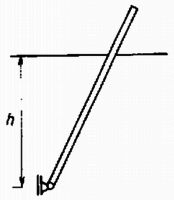

γ = 0, 005 {N/cm}^{3}

, b)

γ = 0, 00853 {N/cm}^{3}

5. ábra

Nagy László

Megoldás. Az egyensúlyt a felhajtóerő és a súlyerő forgatónyomatékainak az egyenlősége jelenti. Jelentse

α

a függőleges helyzettől mért szöget (6. ábra).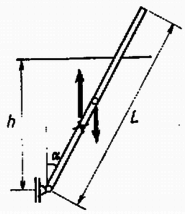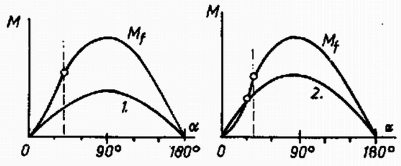

6. ábra

Ha az egész pálca víz alatt van, a felhajtóerő

A L γ_{v}

(

γ_{v}

a víz fajsúlya), az erőkar

(L / 2) sin α

, így a forgatónyomaték (

(A L^{2} γ_{v} / 2) sin α

(7. ábra). Ha

α

0^{\circ}

és

37^{\circ}

közé esik, a pálca egy része kiáll a vízből. Ekkor az előbbi mennyiségek: felhajtóerő:

A h γ_{v} / cos α

, erőkar:

(μ / 2) tg α

forgatónyomaték:

(A h^{2} γ_{v} tg α) / (2 cos α)

(

M_{f}

görbe a 7. ábrán).

7. ábra

A súlyerő forgatónyomatéka [az

A L γ

súlyerő és az

(L / 2) sin α

erőkar szorzata:

(A L^{2} γ / 2) sin α

] mindvégig sinusfüggvény szerint alakul, amelynek amplitúdóját a bot fajsúlya szabja meg.
Amíg a bot fajsúlya kicsiny, a

{(h / L)}^{2} γ_{v} = 0, 64 γ_{v}

érték alatt van, a súly forgatónyomatékának görbéje (1.) teljesen az

M_{f}

görbe alatt van (l. a 7. ábrát). Ez a határ onnan adódik, hogy ekkor indul

M_{f}

görbéje és a súlyerő forgatónyomatékának görbéje egyenlő iránytangenssel. Az 1. görbének és

M_{f}

-nek két metszéspontja van az

α = 0

és az

α = 180^{\circ}

helyeken. Az első helyzet a stabilis, mert ekkor kis kimozduláskor

M_{f}

gyorsabban növekszik, mint 1. Ez a mi esetünk is,

γ = 0, 5 γ_{v}

-nél. Az

α = 180^{\circ}

-hoz tartozó egyensúlyi helyzet labilis.
Ha a bot fajsúlya

{(h / L)}^{2} γ_{v}

és

γ_{v}

között van, akkor a súlyerő forgatónyomatékának a görbéje egy harmadik metszéspontot is ad

M_{f}

görbéjének kezdeti, behorpadt részén:

\begin{matrix} \frac{A L^{2} γ sin α}{2} = \frac{A h^{2} γ_{v} tg α}{2 cos α} . \end{matrix}

Ennek megoldása

α

-ra:

cos α = \frac{h}{L} \sqrt[]{\frac{γ_{v}}{γ}} = 0, 866

α = 30^{\circ}

. Ez a felelet a második kérdésre; a bot részben kiáll a vízből stabilis egyensúlyi helyzetben, mert a vizsgálat azt mutatja, hogy balra‐jobbra történő kis kimozdulások után a forgatónyomatékok visszaviszik ebbe a helyzetbe a botot. Épp így megmutatható, hogy a

0^{\circ}

-hoz és

180^{\circ}

-hoz tartozó egyensúlyi helyzetek labilisak.
Ha a bot fajsúlya nagyobb, mint

γ_{v}

, akkor a súly forgatónyomatékának a görbéje

M_{f}

görbéje fölé emelkedik és csak

α = 180^{\circ}

-nál ad stabilis egyensúlyi helyzetet: a bot függőlegesen lefelé lóg.

A = 20 cm \cdot 20 cm

alapterületű, fekvő négyzetes oszlopban vastag, elhanyagolható súlyú dugattyú zár el

3200 {cm}^{3}

higanyt és

800 {cm}^{3}

levegőt. A külső levegő nyomása

10 {N/cm}^{2}

(azaz

73, 5 cm

-es higanyoszlop nyomása). A higany fajsúlya

0, 136 {N/cm}^{3}

. Hol helyezkedik el a dugattyú, ha a négyzetes oszlopot (8. ábra) függőleges helyzetbe hozzuk a) nyitott végével felfelé és b) nyitott végével lefelé?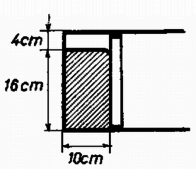

8. ábra

(Vermes Miklós)

Megoldás. A lényeges pont a levegő nyomásának a meghatározása a kezdeti állapotban. A 400 cm

^{2}

területű dugattyút a külső levegő 4000 N erővel nyomja. A higanyoszlop hidrosztatikai nyomása a fenéken

16 \cdot 13, 6 \cdot 0, 01 {N/cm}^{2}

. Átlagban ennek a felével kell számolnunk és ez

20 \cdot 16 {cm}^{2} = 320 {cm}^{2}

területen

0, 5 \cdot 16 \cdot 13, 6 \cdot 0, 01 \cdot 320 N = 348, 16 N

erőt ad. A bezárt levegő nyomása a higanyon keresztül átadódik a dugattyúnak és a helyzet olyan, mintha a levegő

p

nyomása az egész 400 cm

^{2}

-nyi felületet nyomná. Az erők egyenlősége: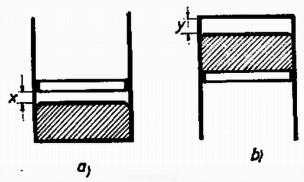

\begin{matrix} 348, 16 N + 400 {cm}^{2} p = 4000 N . \end{matrix}

9. ábra

Innen a bezárt levegő nyomása:

p = 9, 1 {N/cm}^{2}

. Az

a)

esetben (9a. ábra) a higany nem számít; Boyle‐Mariotte törvényéből

x = 1, 8 cm

. A

b)

esetben (9b. ábra) a külső légköri levegő nyomásából levonandó a 8 cm magas higanyoszlop

8 \cdot 0, 136 {N/cm}^{2} = 1, 09 {N/cm}^{2}

nyomása; Boyle‐Mariotte törvényével

y = 2, 05 cm

A II. forduló feladatai

1. Az

R = 1, 4 méter

sugarú gömbhéj belső felületén kis test mozog súrlódásmentesen (10. ábra). Sebessége

h_{1} = 0, 1 méter

magasságban a legnagyobb,

h_{2} = 0, 3 méter

magasságban a legkisebb. Mekkorák ezek a sebességek?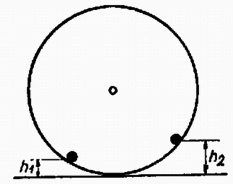

10. ábra

(Dr. Bodó Zoltán)

Megoldás. Abból, hogy

v_{1}

a legnagyobb, illetve

v_{2}

a legkisebb, következik, hogy mindkét sebesség vízszintes irányú.
Az egyik egyenletet az energiatörvény adja:

\begin{matrix} m g h_{1} + m v_{1}^{2} / 2 = m g h_{2} + m v_{2}^{2} / 2. \end{matrix}

(1)

11. ábra

Nézzük a test helyzetét felülnézetben is (11. ábra). A testre ható kényszererő a középpont felé hat, a súlyerő függőleges. Tehát a vízszintes síkra vetített mozgást nézve nincs forgatónyomaték. Ilyenkor a vetületre érvényes a területi sebesség állandóságának (az impulzusnyomaték, perdület állandóságának) törvénye. A vetületben a vezérsugarak

R cos α

és

R cos β

, továbbá az ábra alapján

\begin{matrix} cos α & = \frac{\sqrt[]{R^{2} - {(R - h_{1})}^{2}}}{R} = \frac{\sqrt[]{2 R h_{1} - h_{1}^{2}}}{R}, \\ cos β & = \frac{\sqrt[]{R^{2} - {(R - h_{2})}^{2}}}{R} = \frac{\sqrt[]{2 R h_{2} - h_{2}^{2}}}{R} . \end{matrix}

A területi sebesség állandóságát kifejező

\begin{matrix} v_{1} R cos α = v_{2} R cos β \end{matrix}

összefüggésbe helyettesítve

\begin{matrix} v_{1} \sqrt[]{2 R h_{1} - h_{1}^{2}} = v_{2} \sqrt[]{2 R h_{2} - h_{2}^{2}} . \end{matrix}

(2)

A kapott egyenletrendszer megoldása:

\begin{matrix} v_{1} & = \sqrt[]{2 g h_{2} \cdot \frac{2 R - h_{2}}{2 R - (h_{1} + h_{2})}} = 2, 5 m/s, \\ v_{2} & = \sqrt[]{2 g h_{1} \cdot \frac{2 R - h_{1}}{2 R - (h_{1} + h_{2})}} = 1, 5 m/s . \end{matrix}

Néhány lényeges megjegyzést kell tenni. A területi sebesség állandóságának törvényét a vetületben csak annak megállapítása után szabad alkalmazni, hogy az erőknek (a vetület szempontjából) nincs forgónyomatékuk. Akármilyen körben járkáló szerkezetre nem volna szabad alkalmazni az említett törvényt. A feladat a mechanikából ismert úgynevezett gömbinga. Egyáltalán nem igaz, hogy a pálya legalacsonyabb és legmagasabb pontjai a gömb átellenes oldalán vannak. Ilyen állítást nem is használtunk fel.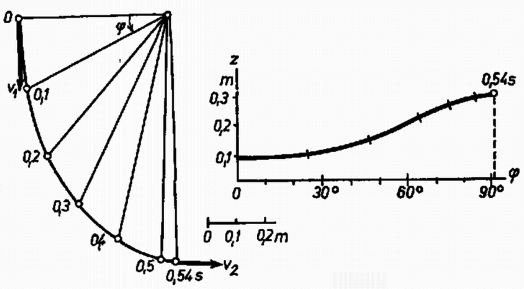

12. ábra

A mechanika törvényeit századmásodpercről századmásodpercre numerikus számításban alkalmazva, nyomon követhetjük a gömbinga mozgását. A 12. ábra feladatunk adatai mellett először felülnézetben, vízszintes vetületben mutatja a pályát. A test

91^{\circ}

-os vezérsugár‐elfordulás után,

0, 54

s múlva ér legmagasabb pontjára, azután újra lefelé megy. Így hullámozva jár két szélességi kör között. A jobb oldali rajz az elért magasságot a szögelfordulás függvényében mutatja. A pálya természetesen nem síkgörbe.

2. Vízszintes lapon egy henger és egy kocka mozoghat, miközben a henger egy alkotója mentén érintkezik a kockával (13. ábra). A henger átmérője egyenlő a kocka oldalélével, a két test tömege is egyenlő. Mindegyik felületen a tapadási súrlódási együttható

μ_{0}

, a csúszási súrlódási együttható

μ (μ_{0} > μ)

. Mekkora legyen az

F

állandó tolóerő, hogy a két test mozgása közben a kocka gördülés nélkül tolja maga előtt a hengert? Számadatok: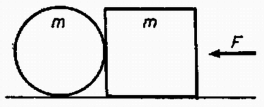

m = 12 kg

μ = 0, 2

μ_{0} = 0, 6

g = 10 {m/s}^{2}

13. ábra

(Légrádi Imre)

Megoldás. Ha a henger gördülés nélkül mozog, akkor alján a csúszó súrlódási együtthatóval számítandó az

S_{1}

súrlódási erő, de ennek jelentkeznie kell a henger és a kocka találkozási élénél is, a hengernél lefelé, a kockánál felfelé, annak súlyát részben kiegyenlítve. A csúszó súrlódási erő a henger aljánál, annak

S_{1}

-gyel növelt súlyát is figyelembe véve (l. a 14. ábrát):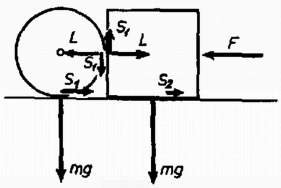

\begin{matrix} S_{1} = μ (m g + S_{1}) . \end{matrix}

14. ábra

Abban a határesetben, amikor még nincs gördülés, a henger és a kocka közös élénél:

\begin{matrix} S_{1} = μ_{0} (m a + S_{1}), \end{matrix}

ugyanis a normális erő a henger gyorsításához és az

S_{1}

fedezéséhez szükséges erők összege. Az egyenletrendszer megoldása:

\begin{matrix} a = \frac{μ}{μ_{0}} \cdot \frac{1 - μ_{0}}{1 - μ} \cdot g, S_{1} = \frac{m g}{1 - μ} . \end{matrix}

A kocka alsó lapján működő súrlódási erő, figyelembe véve

S_{1}

emelő hatását:

\begin{matrix} S_{2} = μ (m g - S_{1}) . \end{matrix}

Mindezek ismeretében az

F

tolóerő:

\begin{matrix} F = m a + S_{1} + m a + S_{2} = m g \cdot \frac{2 μ (1 - μ μ_{0})}{μ_{0} (1 - μ)} = 88 newton . \end{matrix}

Tehát a henger 88 newtonnál nagyobb erő esetében mozog gördülésmentesen. Nyugalomból való induláshoz

2 m g μ_{0} = 144

newtonnál nagyobb erőre van szükség. Ha tehát legalább ekkora erő hatására elindult a szerkezet, akkor 88 newtonig csökkentve az erőt a henger nem gördül. Ennél kisebb erő esetében gördül a henger, de

2 m g μ = 48

newton alatt minden megáll.

3. Az

a_{1}

vastagságú,

n_{1} = 2, 7

törésmutatójú üveglemezre

a_{2}

vastagságú,

n_{2} = 2, 43

törésmutatójú, majd

a_{3}

a_{4}

vastagságú,

n_{3}

n_{4}

törésmutatójú üvegrétegeket helyezünk (15. ábra). Az

A_{1}

A_{2}

A_{3}

pontokból egyszerre induló fénysugarak egyidejűleg érkeznek

B_{2}

B_{3}

B_{4}

pontokba a teljes visszaverődés határszögével.

A_{2} B_{2} = A_{3} B_{3} = A_{4} B_{4} = b = 10 mm

. Mekkora az

a_{1}

a_{2}

a_{3}

rétegek vastagsága és mekkorák az

n_{3}

n_{4}

törésmutatók?
(Vermes Miklós)

Megoldás. Felírjuk az

a_{1}

a_{2}

a_{3}

rétegekre érvényes adatokat.

A fényutak:

b / sin α_{1},

b / sin α_{2},

b / sin α_{3}

A sebességek:

c / n_{1},

c / n_{2},

c / n_{3},

A menetidők:

n_{1} (b / c) sin α_{1} = n_{2} (b / c) sin α_{2} = n_{3} (b / c) sin α_{3}

Teljes visszaverődés folytán:

sin α_{1} = n_{2} / n_{1} sin α_{2} = n_{3} / n_{2} sin α_{3} = n_{4} / n_{3}

Felhasználva ezeket a menetidőknél:

\frac{n_{2}}{n_{1}^{2}} = \frac{n_{3}}{n_{2}^{2}} = \frac{n_{4}}{n_{3}^{2}} = k

Tehát a feladat feltételének olyan törésmutatók felelnek meg, amelyekre

k

állandó. Számadatainkkal

k = 2, 43 / 2, 7^{2} = 1 / 3

.
A feladatban keresett törésmutatók: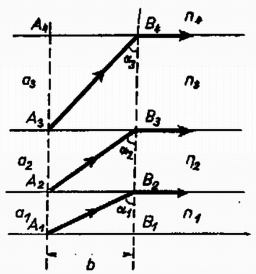

\begin{matrix} n_{3} & = k n_{2}^{2} = k^{3} n_{1}^{4} = 1, 968, \\ n_{4} & = k n_{3}^{2} = k^{7} n_{1}^{8} = 1, 291. \end{matrix}

15. ábra

Így a szögekre a következőket kapjuk:

\begin{matrix} sin α_{1} & = k n_{1} = 0, 9; & α_{1} = 64^{\circ} 09', \\ sin α_{1} & = k^{2} n_{1}^{2} = 0, 81; & α_{2} = 54^{\circ} 06', \\ sin α_{3} & = k^{4} n_{1}^{4} = 0, 6561; & α_{3} = 41^{\circ} 00' . \end{matrix}

A rétegvastagságok:

\begin{matrix} a_{1} & = b ctg α_{1} = b \cdot \frac{\sqrt[]{1 - k^{2} n_{1}^{2}}}{k n_{1}} = 4, 8 mm, \\ a_{2} & = b ctg α_{2} = b \cdot \frac{\sqrt[]{1 - k^{4} n_{1}^{4}}}{k^{2} n_{1}^{2}} = 7, 2 mm, \\ a_{3} & = b ctg α_{3} = b \cdot \frac{\sqrt[]{1 - k^{8} n_{1}^{8}}}{k^{4} n_{1}^{4}} = 11, 5 mm . \end{matrix}

A feladat a száloptika egy problémájának leegyszerűsített alakja. Vékony üvegszálakban, amelyeket fénysugaras hírátvitelre használnak, szükséges, hogy a különböző irányban a szálba egyszerre belépő fénysugarak különböző útjaik ellenére egyszerre érkezzenek meg. Ez elérhető, ha a szálban a középponttól mért távolság négyzetes függvénye szerint csökken a törésmutató.

A III. kísérleti forduló

A III. kísérleti forduló Debrecenben, a Kossuth Lajos Tudományegyetem Kísérleti Fizikai Intézetének rendezésében folyt le. A két feladat közül az egyikben fajhőméréssel, a másikban egy váltakozó áramú tekercs terének kimérésével kellett foglalkozni.