Kezdőlap


Cím:	1978. évi Eötvös Loránd Fizikaverseny
Füzet:	1979/február, 81 - 83. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat 1978. október 28-án rendezte 55. versenyét Budapesten és 11 vidéki városban az 1978-ban érettségizettek és a középiskolai tanulók részére. A versenyzők 5 órai munkaidő alatt oldhattak meg három feladatot és bármilyen segédeszközt használhattak. A beadott dolgozatok száma 396 volt. Ismertetjük a feladatokat és megoldásukat.

L

hosszúságú,

m_{2}

tömegű gerenda apró görgőkön súrlódás nélkül mozoghat a vízszintes padlón. Bal végén

m_{1}

tömegű ember áll. Nyugalomból kiindulva ez az ember állandó

F

erő kifejtésével jobbra szalad. Az ember egy idő múlva a padlóhoz képest

α

szög alatt, a gerendához képest

u

nagyságú sebességgel felugrik. Mikor kell felugrania, hogy éppen a gerenda jobb oldali végére érkezzék ? Számadatok:

m_{1} = 50 kg

m_{2} = 200 kg

F = 80 newton

α = 45^{\circ}

u = 5 m/s

L = 10 m

g = 10 {m/s}^{2}

.
(Radnai Gyula)

Megoldás. Az ember gyorsulása a nyugvó koordináta-rendszerben

a_{1} = F / m_{1}

, az indulástól mért

t

időpillanatban történő elugráskor az ember végsebessége

v_{1} = a_{1} t

, útja

s_{1} = (F / 2 m_{1}) t^{2}

, a gerendáé

a_{2} = F / m_{2}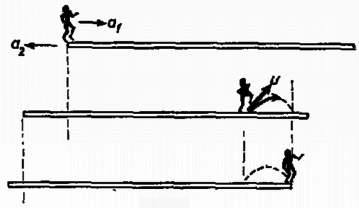

v_{2} = a_{2} t

s_{2} = (F / 2 m_{2}) t^{2}

(1. ábra).

1. ábra

Az elugrás sebességének függőleges összetevője

u sin α

, a levegőben tartózkodás ideje

t_{0} = (2 u / g) sin α

. Az elugrás vízszintes összetevője a gerendához képest

u cos α

. Az ugró sebessége a háttérhez képest

u cos α - (F / m_{2}) t

. Az impulzustörvény szerint ekkor a gerenda sebessége ellentétes irányban:

\begin{matrix} \frac{m_{1}}{m_{2}} (u cos α - \frac{F}{m_{2}} \cdot t) . \end{matrix}

Az ugrás ideje alatt a gerenda még megtesz

\begin{matrix} \frac{m_{1}}{m_{2}} (u cos α - \frac{F}{m_{2}} \cdot t) \cdot \frac{2 u sin α}{g}, \end{matrix}

az ugró

\begin{matrix} (u cos α - \frac{F}{m_{2}} \cdot t) \cdot \frac{2 u sin α}{g} \end{matrix}

távolságot. Az elugrás pillanatától számított, még hátralevő távolság:

\begin{matrix} L - \frac{F}{2 m_{1}} \cdot t^{2} - \frac{F}{2 m_{2}} \cdot t^{2} . \end{matrix}

Az ugrás ideje alatt a gerenda és az ember által megtett távolságok összege egyenlő a még hátralevő távolsággal. Ezt az egyenlőséget felírva és az egyenletet rendezve kapjuk:

\begin{matrix} \frac{F}{2} \cdot t^{2} - \frac{2 F u sin α \cdot m_{1}}{m_{2} g} \cdot t - [\frac{m_{1} m_{2}}{m_{1} + m_{2}} \cdot L - \frac{u^{2} m_{1} sin 2 α}{g}] = 0. \end{matrix}

Innen:

\begin{matrix} t = \frac{2 u sin α}{g} \cdot \frac{m_{1}}{m_{2}} + \sqrt[]{\frac{4 u^{2} sin^{2} α}{g^{2}} {(\frac{m_{1}}{m_{2}})}^{2} + \frac{2 m_{1}}{F} [\frac{m_{2} L}{m_{1} + m_{2}} - \frac{u^{2} sin 2 α}{g}]} . \end{matrix}

Számadatainkkal

t = 2, 8 s

2. Egy üvegedényben higany van, amelybe üveg kapilláris nyúlik (2. ábra). A higanyra a földhöz képest nagy feszültséget kapcsolunk. Elmozdul-e a hajszálcsőben a higany, és ha igen, merre ?
(Károlyházy Frigyes)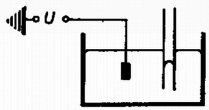

2. ábra

Megoldás. Egy töltött fémtesten a töltések a felszínen helyezkednek el. A felszín minden pontjában merőlegesen kifelé toló erő működik, amelyet a felszín többi töltése fejt ki, és amely erő arányos a felszíni töltéssűrűséggel (3. ábra). A felületi töltéssűrűség a mértani alaktól függ. A mi higanyunk alakját a 3. ábra jobb oldali rajza mutatja. A higany a hajszálcsőben lesüllyed, a felület ezen helyén gyakorlatilag nincs töltés, mert ez a hely szinte a fémtest belsejében van. A higany felszínének többi részén a taszítóerő kifelé viszi a higanyt. A higany térfogata adott, tehát a kapillárisban lesüllyed a szint.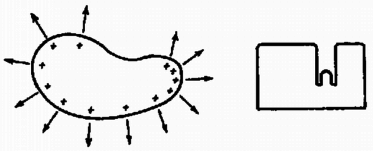

3. ábra

3. Egy zárt doboznak négy egyforma kivezetése van (4. ábra). Belsejében egy-egy ellenállás, önindukciós tekercs, kondenzátor és dióda van csillagkapcsolásban. A kivezetések nincsenek megjelölve. Rendelkezésünkre áll (biztosítékokkal együtt) egy generátor, amely egy meghatározott, ismert frekvenciájú váltófeszültséget ad, továbbá egy váltóáramú voltmérő és egy váltóáramú ampermérő. Határozzuk meg az ellenállás, az önindukciós együttható és a kapacitás nagyságát!
(Vermes Miklós)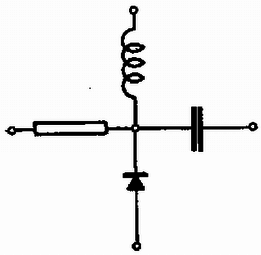

4. ábra

Megoldás. Először meg kell találnunk, hogy melyik kivezetés melyik alkatrészhez tartozik. Felmerülhet az a gondolat, hogy a dióda és tekercs sorba kapcsolása esetén az áram végtelen lesz, mert a dióda által átengedett áram egyenáramú összetevője nem talál ohmos ellenállásra. Ez azonban tévedés. Ha sorba kapcsolt tekercsre és diódára

U = U_{0} sin ω t

váltófeszültséget kapcsolunk, akkor az átmenő áram

I = \frac{U_{0}}{ω L} (1 - cos ω t)

. Ugyanis ebben az esetben lesz az önindukciós feszültség

U = L \cdot \frac{d I}{d t} = U_{0} sin ω t

(5. ábra), és ekkor teljesül az

I \geq 0

fel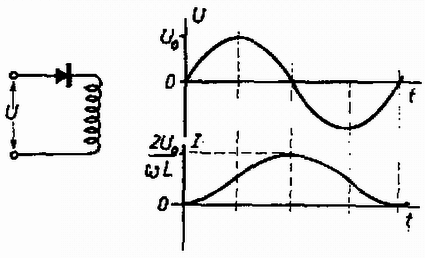tétel.

5. ábra

Diódával sorbakapcsolt kondenzátor nem enged át váltóáramot, mert a kondenzátor feltöltődik a váltófeszültség csúcsfeszültségére és ezután a dióda jelenléte miatt nem folyhat ki belőle töltés. Tehát meg kell keresni azt a kivezetést, amely egy másikkal együtt semmi áramot sem enged át. Ezek egyike a kondenzátor, a másik a dióda. A kondenzátor kivezetése e kettő közül úgy határozható meg, hogy megkeressük, melyik kivezetéshez tartozó alkatrészt lehet az ellenálláson vagy tekercsen keresztül maradandóan feltölteni (többszöri próbálkozással).
Végül a legnehezebb a tekercs és ellenállás kivezetéseinek megkülönböztetése. A kondenzátort sorba kapcsoljuk az egyik ismeretlen alkatrésszel és lemérjük a váltóáramú ellenállást műszereinkkel. Ezután az ismeretlen ellenállás mellé kapcsoljuk a másikat (6. ábra). A tekercsnek az ellenállás mellé kapcsolása mindenképp csökkenti az eredő váltóáramú ellenállást, amint arról számítással meggyőződhetünk.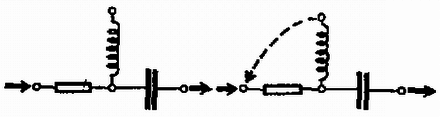

6. ábra

A kivezetéseket ismerve két-két kivezetés közötti impedanciamérésekkel megkapjuk a keresett adatokat.

A verseny eredménye

I. díj nem került kiosztásra. II. díjat hárman kaptak egyenlő helyezéssel: Balogh Elek, a dömösi építőipari szövetkezet dolgozója (Esztergomban, a Dobó Katalin Gimnáziumban érettségizett Sipos Imre tanítványaként), Lukács József (Bp., József Attila Gimn, IV. o. t., tanára Tóth Eszter) és Ujházy András, az MTA Enzimológiai Intézetének dolgozója (Budapesten, a József Attila Gimnáziumban érettségizett Tóth Eszter tanítványaként). III. díjat hárman kaptak egyenlő helyezésben: Kaufmann Zoltán (Vác, Sztáron Sándor Gimn. IV. o. t., tanára Molnár Sándorné), Németh Gábor honvéd (Budapesten, a József Attila Gimnáziumban érettségizett Tóth Eszter tanítványaként) és Szarka László (Székesfehérvár, József Attila Gimn. IV. o. t., tanára Teleki Sándorné).