Cím:	1979. A XXI. Nemzetközi Matematikai Diákolimpia feladatai
Füzet:	1979/szeptember, 3 - 5. oldal	PDF  |  MathML
Témakör(ök):	Nemzetközi Matematikai Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   1. Legyenek $p$ és $q$ olyan természetes számok, amelyekre fennáll, hogy $\begin{array}{c}{\displaystyle \frac{p}{q}=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\text{...}-\frac{1}{1318}+\frac{1}{1319}\mathrm{.}}\end{array}$ Bizonyítsa be, hogy $p$ osztható $1979$-cel. (NSZK, 6 pont)${}^{*}$   2. Adva van egy ötoldalú hasáb: alaplapja az $A_1{A}_2{A}_3{A}_4{A}_5$, fedőlapja pedig a $B_1{B}_2{B}_3{B}_4{B}_5$ ötszög. E két ötszög mindegyik oldalát, továbbá valamennyi $A_i{B}_j$ szakaszt $\left(i\mathrm{,}j=\mathrm{1,}\mathrm{2,}\text{...}\mathrm{,}5\right)$ vörösre vagy zöldre színezzük. Minden olyan háromszögnek, amelynek csúcsai egyúttal a hasáb csúcspontjai is, és amelynek mindegyik oldala színezett, van két különböző színű oldala. Mutassa meg, hogy ekkor az alaplapnak és a fedőlapnak összesen tíz oldala mind egyforma színű. (Nagy-Britannia, 7 pont)   3. Adva van a síkban két egymást metsző körvonal: $k_1$ és $k_2$. Jelölje $A$ a két metszéspont egyikét. Két tömegpont: $P_1$ és $P_2$ mozog $k_1$-en, illetve $k_2$-n állandó sebességgel ugyanabban a forgási irányban. Mozgásukat egy időben kezdik az $A$ pontban, és egy-egy körüljárás után ismét egyidejűleg érkeznek az $A$ pontba. Bizonyítsa be, hogy van a síkban olyan rögzített $P$ pont, amelyre a mozgás minden időpontjában érvényes a $\begin{array}{c}{\displaystyle P{P}_1=P{P}_2}\end{array}$ egyenlőség. (Szovjetunió, 7 pont)   4. Adva van a $\Pi$ síkban egy $P$ és a $\Pi$ síkon kívül egy $Q$ pont. Határozza meg a $\Pi$ síknak valamennyi olyan $R$ pontját, amelyre a $\begin{array}{c}{\displaystyle \frac{QP+PR}{QR}}\end{array}$ hányados értéke maximális. (USA,  6 pont)   5. Határozza meg az összes $a$ valós számot, amelyekhez léteznek a $\begin{array}{c}{\displaystyle \sum _{k=1}^{5}k{x}_k=a\mathrm{,}\sum _{k=1}^5{k}^3{x}_k=a^2\mathrm{,}\sum _{k=1}^5{k}^5{x}_k=a^3}\end{array}$ egyenlőségeket kielégítő $x_1$, $x_2$, $x_3$, $x_4$ és $x_5$ nemnegatív valós számok. (Izrael, 7 pont)   6. Legyen $A$ és $E$ egy szabályos nyolcszög két átellenes csúcsa. Egy béka az $A$ csúcsból kiindulva kezd ugrálni. A nyolcszög bármely csúcsából ‐ az $E$-t kivéve ‐ a mellette levő egyik csúcsba ugorhat. Ha az $E$ csúcsba ér, akkor megáll, és ott marad. Legyen $a_n$ a pontosan $n$ ugrásból álló különböző utak száma. Bizonyítsa be, hogy $a_{2n-1}=0$, $a_{2n}=\frac{1}{\sqrt[]{2}}\left(x^{n-1}-y^{n-1}\right)$, $n=\mathrm{1,}\mathrm{2,}\mathrm{3,}\text{...}$, ahol $x=2+\sqrt[]{2}$ és $y=2-\sqrt[]{2}$. Megjegyzés: Egy pontosan $n$ ugrásból álló út a csúcsoknak olyan $P_0\mathrm{,}{P}_1\mathrm{,}\text{...}\mathrm{,}{P}_n$ sorozata, amely eleget tesz az alábbi feltételeknek: I. $P_0=A$, $P_n=E$; II. minden, $0\le i\le n-1$ egyenlőtlenséget kielégítő $i$-re $P_i$ különbözik $E$-től; III. minden, $0\le i\le n-1$ egyenlőtlenséget kielégítő $i$-re $P_i$ és $P_{i+1}$ szomszédos csúcsok. (NSZK, 7 pont)   *   A zsüri az egyetlen különdíjat a 3. feladat különösen elegáns és egyszerű megoldásáért LE BA KHANH TRINH 17 éves vietnami versenyzőnek adta ki. Az alábbi megoldás az ő dolgozatának alapján készült.   3. Adva van a síkban két egymást metsző körvonal: $k_1$ és $k_2$. Jelölje $A$ a két metszéspont egyikét. Két tömegpont: $P_1$ és $P_2$ mozog $k_1$-en, illetve $k_2$-n állandó sebességgel ugyanabban a forgási irányban. Mozgásukat egyidőben kezdik az $A$ pontban, és egy-egy körüljárás után ismét egyidejűleg érkeznek az $A$ pontba. Bizonyítsa be, hogy van a síkban olyan rögzített $P$ pont, amelyre a mozgás minden időpontjában érvényes a $\begin{array}{c}{\displaystyle P{P}_1=P{P}_2}\end{array}$ egyenlőség.   Megoldás. Jelöljük a $k_1$, ill. $k_2$ körök középpontját $O_1$-gyel, ill. $O_2$-vel, a két kör $A$-tól különböző metszéspontja legyen $B$. Először megmutatjuk, hogy a $P_1$, $P_2$, $B$ pontok a mozgás bármely pillanatában egy egyenesen vannak. Ehhez figyeljük meg a következőket: ha az $A{B}_1{C}_1\mathrm{,}A{B}_2{C}_2\mathrm{,}A{B}_3{C}_3\mathrm{,}\text{...}$ hasonló, és egyező körüljárású háromszögeknél a $B_1\mathrm{,}{B}_2\mathrm{,}{B}_3\mathrm{,}\text{...}$ pontok egy egyenesen vannak, akkor a $C_1\mathrm{,}{C}_2\mathrm{,}{C}_3\mathrm{,}\text{...}$ pontok is egy egyenesen fekszenek. Ez egyszerűen következik abból, hogy a $B_1\mathrm{,}{B}_2\mathrm{,}{B}_3\mathrm{,1}\text{...}$ pontokat az $A$ középpontú, $B_{1}A{C}_1$ szögű és $AC/AB$ arányú forgatvanyújtás viszi át rendre a $C_1\mathrm{,}{C}_2\mathrm{,}{C}_3\mathrm{,}\text{...}$ pontokba, és a forgatvanyújtás egyenestartó. Ez igaz abban az esetben is, ha a hasonló háromszögek helyett egy egyenesbe eső hasonló ponthármasokat mondunk. 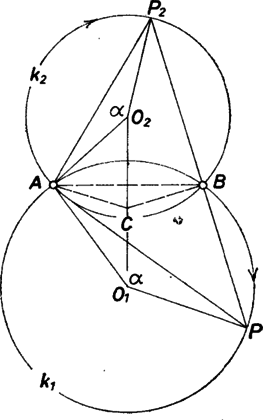    1. ábra   A feladat feltétele szerint a $P_1$, $P_2$  pontok a körök középpontjai körül állandó szögsebességgel forognak. Tegyük fel, hogy pl. a kiindulási $A$ helyzettől $\alpha$ szöggel fordultak el $\left(0<\alpha <2\pi \right)$ (1. ábra). Az $A{O}_1{P}_1$, $A{O}_2{P}_2$ egyező körüljárású, hasonló, egyenlő szárú (esetleg elfajult) háromszögek. Mivel az $O_1{O}_2$ egyenes az $AB$ szakasz felező merőlegese, szerkeszthetünk rajta olyan $C$ pontot, hogy az $ACB$ és $A{O}_1{P}_1$ háromszögek hasonlóak és egyező körüljárásúak legyenek. Előző megjegyzésünk értelmében így a $P_1$, $P_2$, $B$ pontok valóban egy egyenesen vannak, mivel $O_1$, $O_2$, $C$ is egy egyenesen fekszenek. Elegendő most már azt bizonyítanunk, hogy a $P_1{P}_2$ szakasz felező merőlegese ‐ a $P_1{P}_2$ szakasz elhelyezkedésétől függetlenül ‐ átmegy egy rögzített ponton. Messe az $AB$-re $A$-ban állított merőleges a $k_1$, ill. $k_2$ kört $X$-ben, ill. $Y$-ban, és legyen $XY$ felezőpontja $P$ (2. ábr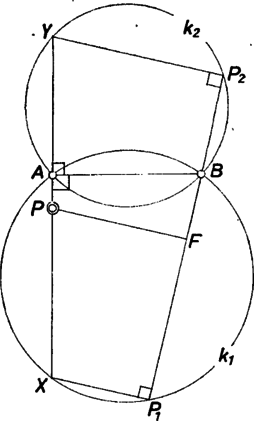a).     2. ábra   A $BX$ és $BY$ szakaszok Thalész tétele szerint köreikben átmérők, ezért az $X{P}_1{P}_2\sphericalangle$ és $Y{P}_2{P}_1\sphericalangle$ derékszög, az $X{P}_1{P}_{2}Y$ négyszög tehát derékszögű trapéz (hurkolt is lehet, és derékszögű háromszöggé is fajulhat). Következésképpen a $P_1{P}_2$ szár felező merőlegese átmegy a rögzített $XY$ szár $P$ felezési pontján; ezzel állításunkat igazoltuk. ${}^{*}$A zárójelben a javasló ország neve és a kapható maximális pontszám szerepel.