A 2194. feladatban azt kellett igazolni, hogy tetszőleges $a\mathrm{,}b\mathrm{,}c$ valós számra az

a)haλ>0tetszőleges szám, akkorh(λa,λb,λc)=h(a,b,c);b)h(a,b,c)=h(-a,-b,-c)=h(-a,b,c);c)h(a,b,c)>0,5877,sőt habésckülönböző előjelűek, akkorh(a,b,c)≥3/2.

 

Az a) állítás abból következik, hogy $g\left(x\right)$ értéke nem változik, ha benne $a\mathrm{,}b\mathrm{,}c$ helyébe rendre $\lambda a\mathrm{,}\lambda b\mathrm{,}\lambda c$-t teszünk. b) igazolásához tegyük fel, hogy $g_{a\mathrm{,}b\mathrm{,}c}\left(x\right)$ maximumát $x_0$-nál (is) felveszi, azaz

$\begin{array}{c}{\displaystyle g_{a\mathrm{,}b\mathrm{,}c}\left(x\right)\le g_{a\mathrm{,}b\mathrm{,}c}\left(x_0\right)=h\left(a\mathrm{,}b\mathrm{,}c\right)}\end{array}$

tetszőleges $x$-re. Könnyen ellenőrizhető (2) alapján, hogy

${\displaystyle \begin{array}{cc}\hfill {\displaystyle g_{-a\mathrm{,}-b\mathrm{,}-c}\left(x\right)}& {\displaystyle =g_{a\mathrm{,}b\mathrm{,}c}\left(-x\right)}\hfill \\ \hfill {\displaystyle g_{-a\mathrm{,}b\mathrm{,}c}\left(x\right)}& {\displaystyle =g_{a\mathrm{,}b\mathrm{,}c}\left(x-\pi \right)\mathrm{,}}\hfill \end{array}}$

így tetszőleges $x$-re

$\begin{array}{c}{\displaystyle g_{-a\mathrm{,}-b\mathrm{,}-c}\left(x\right)=g_{a\mathrm{,}b\mathrm{,}c}\left(-x\right)\le g_{a\mathrm{,}b\mathrm{,}c}\left(x_0\right)\mathrm{,}}\end{array}$

és egyenlőség áll $x=-x_0$ esetén, ami igazolja a $h\left(-a\mathrm{,}-b\mathrm{,}-c\right)=h\left(a\mathrm{,}b\mathrm{,}c\right)$ összefüggést. Hasonlóan

$\begin{array}{c}{\displaystyle g_{-a\mathrm{,}b\mathrm{,}c}\left(x\right)=g_{a\mathrm{,}b\mathrm{,}c}\left(x-\pi \right)\le g_{a\mathrm{,}b\mathrm{,}c}\left(x_0\right)\mathrm{,}}\end{array}$

és egyenlőség áll $x=x_0+\pi$ esetén, ami b) másik felét adja.
Az a) és b) állítások alapján $h$ értékkészletének vizsgálatához elegendő az olyan $a\mathrm{,}b\mathrm{,}c$ számhármasokra szorítkoznunk, amelyeknél $|a|+|b|+|c|=1$ és $a\ge 0$, $b\ge 0$. A továbbiakban ezt mindig feltesszük.
Ha $b$ és $c$ különböző előjelűek, akkor b) alapján feltehetjük, hogy $a\ge 0$, $b>0$, $c<0$ és ekkor

$\begin{array}{c}{\displaystyle h\left(a\mathrm{,}b\mathrm{,}c\right)\ge g_{a\mathrm{,}b\mathrm{,}c}\left(\frac{\pi }{3}\right)=\frac{a\cdot \frac{\sqrt[]{3}}{2}+b\cdot \frac{\sqrt[]{3}}{2}+c\cdot \left(-\frac{\sqrt[]{3}}{2}\right)}{a+b-c}=\frac{\sqrt[]{3}}{2}\mathrm{,}}\end{array}$

ha pedig $b$ és $c$ egyező előjelűek, akkor $a\ge 0$, $b\ge 0$, $c\ge 0$ és

$\begin{array}{c}{\displaystyle h\left(a\mathrm{,}b\mathrm{,}c\right)\ge g_{a\mathrm{,}b\mathrm{,}c}\left(\frac{\pi }{5}\right)=\frac{a\text{sin}\frac{\pi }{5}+b\text{sin}\frac{2\pi }{5}+c\text{sin}\frac{4\pi }{5}}{a+b+c}\ge \text{sin}\frac{\pi }{5}>0\mathrm{,}\mathrm{5877,}}\end{array}$

hiszen

$\begin{array}{c}{\displaystyle \text{sin}\frac{\pi }{5}=\text{sin}\frac{4\pi }{5}=\sqrt[]{\frac{5-\sqrt[]{5}}{8}}\text{<span style="font-weight: normal;font-style: normal;">és</span>}\text{sin}\frac{2\pi }{5}=\text{sin}\frac{\pi }{5}\cdot \frac{\sqrt[]{5}+1}{2}>\text{sin}\frac{\pi }{5}\mathrm{.}}\end{array}$

Ezzel a 2194. feladat állításánál, miszerint ${\lambda }_0\ge 0\mathrm{,}5$, többet is igazoltunk, nevezetesen azt, hogy ${\lambda }_0>0\mathrm{,}5877$.
Abból, hogy $h\left(\mathrm{1,}\mathrm{0,}0\right)=h\left(\mathrm{0,}\mathrm{1,}0\right)=h\left(\mathrm{0,}\mathrm{0,}1\right)=1$, azonnal következik ${\lambda }_0\le 1$. Hogy ${\lambda }_0$-ra egy kicsit jobb felső becslést kapjunk, tekintsük a

$\begin{array}{c}{\displaystyle 4\text{sin}x+2\text{sin}2x+\text{sin}4x}\end{array}$

(3)

függvényt. Állítjuk, hogy ennek értéke legfeljebb $6$, azaz

$\begin{array}{c}{\displaystyle h\left(\frac{4}{7}\mathrm{,}\frac{2}{7}\mathrm{,}\frac{1}{7}\right)\le \frac{6}{7}\mathrm{,}\text{<span style="font-weight: normal;font-style: normal;">amiből</span>}{\lambda }_0\le \frac{6}{7}<\frac{\sqrt[]{3}}{2}\mathrm{.}}\end{array}$

Valóban, ha egy $x$ értékre $\text{sin}x$, $\text{sin}2x$ és $\text{sin}4x$ nem mind pozitív, (3) értéke legfeljebb $4+2=6$. Ha pedig mind pozitív, akkor $2k\pi \le x\le 2k\pi +\frac{\pi }{4}$ valamilyen $k$ egész számra, de ekkor $\text{sin}x\le \frac{\sqrt[]{2}}{2}$, azaz (3) értéke nem több, mint $2\sqrt[]{2}+2+1<6$, ahogyan állítottuk.

 

 

 

1. ábra

 

A c) állítás értelmében $h\left(a\mathrm{,}b\mathrm{,}c\right)\ge \frac{\sqrt[]{3}}{2}$ ha $b$ és $c$ különböző előjelű, most pedig azt kaptuk, hogy ${\lambda }_0<\frac{\sqrt[]{3}}{2}$. Ez azt jelenti ‐ az a) és b) állításokkal együtt ‐, hogy ${\lambda }_0$ meghatározásához elegendő az $a+b+c=1$, $a\ge 0$, $b\ge 0$, $c\ge 0$ feltételeknek eleget tevő számhármasokat vizsgálni.
Térjünk vissza a (2) alatt definiált $g_{a\mathrm{,}b\mathrm{,}c}$ függvényhez, melynek alakja a fenti feltételek mellett

$\begin{array}{c}{\displaystyle g_{a\mathrm{,}b\mathrm{,}c}\left(x\right)=a\text{sin}x+b\text{sin}2x+c\text{sin}4x\mathrm{.}}\end{array}$

(4)

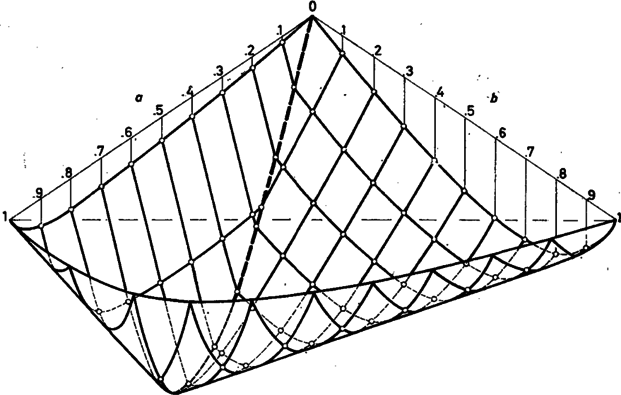
Ennek a függvénynek a $\left[\mathrm{0,2}\pi \right)$ intervallumban (általában) 4 lokális maximuma van, és e négy helyen felvett érték maximuma adja meg $h\left(a\mathrm{,}b\mathrm{,}c\right)$ értékét. Most ha $a\mathrm{,}b\mathrm{,}c$ értékét folyamatosan változtatjuk, akkor a (4) függvény lokális maximumhelyei, valamint az ott felvett értékek is $a\mathrm{,}b\mathrm{,}c$-vel együtt folytonosan, sőt differenciálható módon változnak. Azonban egy furcsa jelenségnek is szemtanúi lehetünk: lokális maximumok keletkeznek és eltűnnek. Egy lokális maximum eltűnését szemlélteti az 1. ábra. Ahogyan a paraméterek változnak (esetünkben $a$, $b$ és $c$), a maximumhely egyre közelebb kerül egy inflexiós ponthoz, majd mikor összeérnek, a maximum eltűnik. Így ha egy síkbeli koordináta-rendszer $\left(a\mathrm{,}b\right)$ koordinátájú pontja fölé a térben a $g_{a\mathrm{,}b\mathrm{,}1-a-b}\left(x\right)$ függvény lokális maximumainak értékeit felrajzoljuk, ,,sima'' felületeket kapunk. A felületek metszik is egymást, ilyenkor $g\left(x\right)$ függvénynek két vagy több egyforma értékű lokális maximuma van. Az abszolút maximumot mindig a legfelső pont képviseli, így ezek a pontok, azaz $h\left(a\mathrm{,}b\mathrm{,}1-a-b\right)$ értékei olyan felületet alkotnak, amely törésvonalak mentén összekapcsolt ,,sima'' felületdarabokból áll.

 

Ez a meggondolás mutatja, hogy a $H\left(a\mathrm{,}b\right)=h\left(a\mathrm{,}b\mathrm{,}1-a-b\right)$ kétváltozós függvény folytonos, de nem minden pontban deriválható (éppen a törésvonalak mentén nem). S mivel folytonos függvény korlátos zárt tartományon felveszi minimumát, azért

${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\lambda }_0=}& {\displaystyle \text{<span style="font-weight: normal;font-style: normal;">min</span>}H\left(a\mathrm{,}b\right)\mathrm{.}}\hfill \\ \hfill {\displaystyle \phantom{=}{}_{a\ge 0\mathrm{,}b\ge 0}}\\ \hfill {\displaystyle \phantom{=}}& {\displaystyle {}_{a+b=1}}\hfill \end{array}}$

 

 

2. ábra

 

Így feladatunk $H\left(a\mathrm{,}b\right)$ minimumának meghatározása. Ezt a felületet mutatja a 2. ábra. A felső háromszöglap (amire az $a$ és $b$ értékeit mutató számok is kerültek) $1$ magasságban van. Látható, hogy két sima felület kapcsolódik egymáshoz a szaggatottal jelölt törésvonal mentén. Azonban azokra az értékekre, amelyeknél $\left(a+b\right)$ $1$-hez közel van, a két felületrész egymásba simul, a törésvonal eltűnik.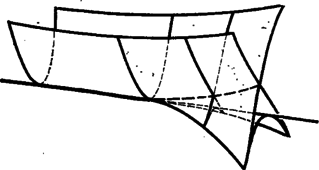

 

 

3. ábra

 

Ebben a pontban a felületnek ún. szingularitása van, a felület tulajdonságai hirtelen, ugrásszerűen megváltoznak. A felületek viselkedését ilyen szinguláris pont környezetében a katasztrófaelmélet vizsgálja. Ha nemcsak az abszolút maximumot, hanem az összes lokális szélsőértéket is berajzoljuk az ábrába, a szinguláris pont környezete (kicsit más nézőpontból) a 3. ábrán láthatóhoz hasonló. A törésvonalat itt is vastag szaggatott vonallal húztuk ki. A felülettípus neve: fecskefarok.

 

 

4. ábra

 

 

5. ábra

 

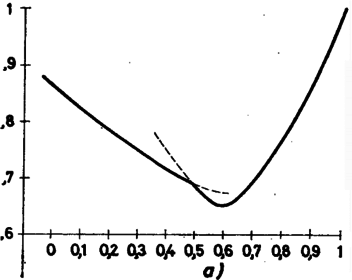
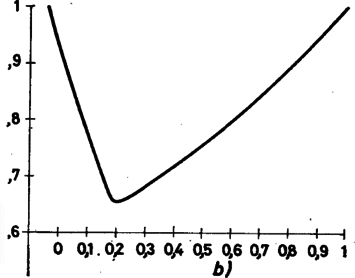
A 4. ábrán az $x$-tengelyen $a$ értékeit mértük fel, az $y$-tengelyen pedig rögzített $a$ mellett a $0\le b\le 1-a$ értékekre $H\left(a\mathrm{,}b\right)$ minimumát (azaz a 2. ábra $b$ tengellyel párhuzamos szintvonalain a legalacsonyabban fekvő pont magasságát). A $0\mathrm{,}5$-nél levő töréspont azt jelzi, hogy ez a minimumhely a sima felületről átkerült a törésvonalra. Hasonlóan az 5. ábrán rögzített $b$ mellett készítettük el a minimumot. Az ábrákról leolvasható, hogy $\lambda \approx 0\mathrm{,}65$ és ezt az értéket az $a_0\approx 0\mathrm{,}6$, $b_0\approx 0\mathrm{,}2$ értékeknél veszi fel. Pontosabb számítások azt mutatják, hogy ${\lambda }_0=0\mathrm{,}659420$, $a_0=0\mathrm{,}6040$, $b_0=0\mathrm{,}1966$. Az ezekhez az értékekhez tartozó $g\left(x\right)$ függvény képét láthatjuk a 6. ábra.

 

 

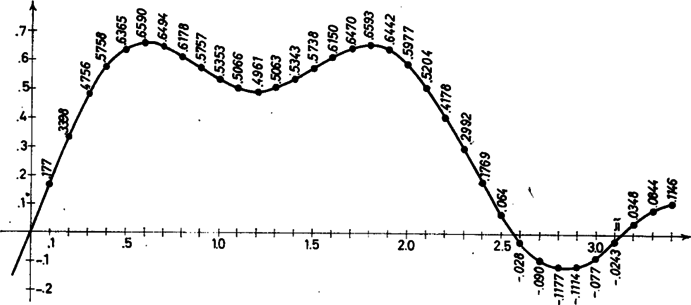6. ábra