Cím: A sík és tér színezései
Szerző(k):  Turán Tamás 
Füzet: 1979/december, 199 - 204. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az alábbiakban a matematika egyik nagyon fiatal fejezetéből ismertetünk néhány eredményt, bizonyítatlan sejtést és problémát.
A bizonyítások leírásánál elsősorban szemléletességre törekedtünk: ezért a precizitás itt-ott csorbát szenved, de úgy véljük, hogy ez a mód a megértést inkább könnyíti majd.
Mivel a szokásos színeket nem tudjuk megjeleníteni, kénytelenek vagyunk három új ,,színt'' kitalálni: a pöttyöt, az ikszet és a kört. Senkit ne tévesszen meg, hogy eme elnevezések feltűnően emlékeztetnek bizonyos nyomdai jelekre ‐ azért ezek színeket jelölnek !

 

A sík színezése két és három színnel
 

Színezzük ki a sík minden pontját, két színt felhasználva, mondjuk pöttyre vagy ikszre.
 

1. Tétel: Bármilyen d távolságot adunk is meg, a 2 színnel ,,kiszínezett síkon'' biztosan lesz két, egymástól d távolságra levő, azonos színű pont.
 

Bizonyítás. Vegyünk fel egy d oldalú szabályos háromszöget a síkon. A háromszög 3 csúcspontjának a kiszínezéséhez csak 2 szín állt rendelkezésre, tehát a 3 pont között van két azonos színű, és ezek d távolságra vannak egymástól.
Ebből a gondolatmenetből látszik, hogy nemcsak egy azonos színű, d távolságú pontpárt találhatunk, hanem végtelen sokat, hiszen a sík bármelyik d oldalú szabályos háromszögéhez tartozik egy ilyen pár.
Vajon igaz marad-e az 1. tétel állítása akkor is, ha a sík pontjainak kiszínezéséhez nem 2, hanem 3 színt használhatunk fel (pötty, iksz, kör) ?
 
 
1. ábra
 

Nézzük meg a 1. ábrát; az ábra 7 pontja között meghúzott összes szakasz d hosszúságú. Legyen mondjuk pötty az A pont színe (továbbiak szempontjából lényegtelen melyik színt választottuk ki A-nak). Ha a B és C, illetve E és F párok egyik tagja nem iksz és a másik nem kör volna, akkor készen is lennénk, hiszen ezek A-val együtt két színnel színezett ponthármast adnának, és emiatt volna köztük két egyszínű. Így feltehetjük, hogy B és C, ill. E és F közül az egyik iksz, a másik kör. De ekkor D-nek is és G-nek is pöttynek kell lennie az előbbi érvelés miatt. Tehát a legrosszindulatúbb színezés esetén is találunk két azonos színű, d távolságra levő pontot, D-t és G-t. Ezzel beláttuk a következő tételt:
 

2. Tétel: A 3 színnel kiszínezett síkon biztosan van 2 azonos színű pont, melyek távolsága d.
 

Hasonló kérdés fogalmazható meg, ha a síkot nem 3, hanem több színnel színezzük ki. Hét színnel már kiszínezhető a sík úgy, hogy van olyan d távolság, amelyhez nem található 2 azonos színű pont, melyek távolsága d. (Ez persze jelenti egyben azt is, hogy n>7 szín esetén ugyanez a helyzet.) Az n=4,5,6 esetben azonban nem tudni a választ, ezek megoldatlan kérdések.
 

Alakzatok létezése
 

Legyen adott a síknak egy tetszőleges színezése, és legyen M egy tetszőleges, pontokból álló alakzat a síkon. A továbbiakban azt mondjuk, hogy az M alakzat a színezésben megtalálható, létezik, ha található a síkon az M alakzattal egybevágó, egyszínű pontokból álló M' alakzat. (A pontalakzatokat a pontok által meghatározott szakaszokkal, távolságokkal fogjuk jellemezni. Tehát, pl. amikor valamely háromszög létezéséről beszélünk, csak a 3 csúcspontjának alakzatát értjük alatta). Vajon a különféle háromszögek szükségképpen léteznek-e a két színnel színezett síkon ?
Az általános kérdésre érdekes módon éppen a legegyszerűbb háromszög, a szabályos esetében adhatunk negatív választ.
 

3. Tétel: Két színnel színezve a síkot, nem biztos, hogy létezik d oldalú szabályos háromszög ‐ vagyis tetszőleges d-hez megadható olyan színezés, amelyben nem létezik d oldalú szabályos háromszög.
 

Bizonyítás. Ilyen színezést mutat a 2. ábra, melyen váltakozó színű, 32d széles, egyik oldalukon nyílt, a másikon zárt sávokat látunk. Rögtön látszik, hogy ha létezne a keresett háromszög, akkor annak egy sávban kellene elférnie. Tegyük fel, hogy mégis van egy d oldalú szabályos háromszög egy ilyen sávban. Toljuk el ezt úgy, hogy a sávhoz tartozó határvonalához legközelebb eső csúcs a határvonalra essen. Azonban a határra került csúcs körül d sugárral rajzolt körnek nincs a sávhoz tartozó 60∘-os középponti szögű íve, így a feltevéssel ellentétben a d oldalú szabályos háromszög nem férhet el egy sávban.
A témával foglalkozó matematikusok ezzel kapcsolatban azt sejtik, hogy a 2. ábrán látható színezés az egyetlen olyan, amelyben nem létezik d oldalú szabályos háromszög ‐ de ez még bizonyításra vár.
 
 
2. ábra
 

Könnyen látható, hogy az adott színezésben minden d'≠d oldalú szabályos háromszög létezik. Ez vezet ahhoz a kevesebbet mondó sejtéshez, mely szerint ha a sík egy színezésében a d oldalú szabályos háromszög nem létezik, akkor minden d'≠d oldalú szabályos háromszög létezik. Ennek a sejtésnek persze csak akkor van jelentősége, ha az előbbi sejtés hamisnak bizonyul, vagyis több olyan színezés van, amelyben nem létezik a d oldalú szabályos háromszög.
 

4. Tétel: A sík két színnel való bármely színezése esetén a d,2d,3d oldalú szabályos háromszögek közül mindig létezik legalább az egyik.
 
 
3. ábra
 

Bizonyítás: Vegyünk fel a síkon két azonos színű pontot, A-t és B-t, melyek távolsága d. (Ilyen pontpár létezését az 1. Tétel biztosítja, 3. ábra). Ezek színe legyen mondjuk pötty. A tőlük szintén d távolságra levő C és D pontok színéről feltehetjük, hogy iksz, mert ellenkező esetben készen vagyunk. Az AB egyenesen a B-től d távolságra levő E pont csak pötty lehet, hiszen a C,D,E pontok 3d oldalú szabályos háromszöget határoznak meg. Az AC egyenesen C-től d távolságra levő F pont csak iksz lehet, hiszen A, E és F pontok 2d oldalú szabályos háromszöget alkotnak. Az FE szakasz G felezőpontja viszont vagy a C és F, vagy a B és E pontokkal azonos színű ponthármast alkot, attól függően, hogy iksz-e vagy pötty.
 

5. Tétel: A két színnel kiszínezett síkon az a,b,c oldalú háromszög akkor és csak akkor létezik, ha az a, b, ill. c oldalú szabályos háromszögek közül legalább az egyik létezik.
Még a tétel bizonyítása előtt megemlítjük, hogy ez a tétel, valamint az előzőleg említett sejtés indokolja azt az általánosabb sejtést, miszerint a sík két színnel való bármely színezésében egy bizonyos szabályos háromszög kivételével tetszőleges háromszög létezik. (Ez a sejtés egyébként az 5. tétel ismeretében ekvivalens a 4. tétel előtt említett sejtéssel.)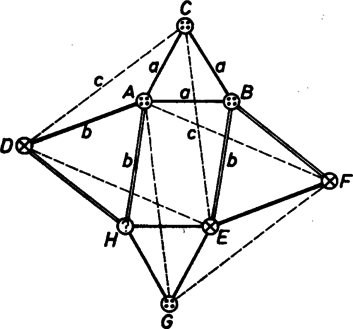
 
 
4. ábra
 

Bizonyítás: Ha, mondjuk, az a oldalú ABC szabályos háromszög létezik a síkon, akkor vegyünk fel egy olyan D pontot, melyre DA=b, CD=c (4. ábra). D-nek C körüli 60∘-os elforgatásával kapjuk az E pontot, amelyre igaz, hogy BCE az ACD-vel egybevágó háromszög. D-t A körül 60∘-kal elforgatva kapjuk H-t. Könnyű belátni, hogy az ABEH pontok paralelogrammát határoznak meg. Az EH, EB oldalakra kifelé szabályos háromszögeket emelve kapjuk a G és F pontokat. Ismét rosszindulatúan próbálunk színezni: ha az A,B,C pontok pöttyök voltak, D iksz legyen, csakúgy, mint E és F, mert az ACD, BCE, BAF háromszögek egybevágóak, mindnek a,b,c nagyságú oldalai vannak. Ha E és F iksz, akkor G pötty legyen, mert a GEF háromszög is egybevágó az előzőekkel. Ha a H pont pötty, akkor az A és G pontokkal, ha iksz; akkor a D és E pontokkal határoz meg a,b,c oldalú, azonos színű háromszöget. Ezzel beláttuk a tétel első felét.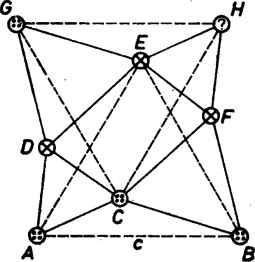
 
 
5. ábra
 

Hátravan még a tétel második fele, a ,,csak akkor'' bizonyítása; vagyis ha létezik az a,b,c oldalú háromszög, akkor létezik az a, b, ill. c oldalú szabályos háromszögek közül legalább az egyik. Legyen ABC az a háromszög, amelynek minden csúcsa pötty, és rajzoljunk hozzá egy, a 4. ábrán láthatóhoz hasonló alakzatot (5. ábra), vagyis válasszuk a CDEF paralelogrammát úgy, hogy az oldalakra kifelé írt szabályos háromszögeknek A, G, H és B legyenek a csúcsai. Ebben D csak iksz lehet, E szintén, hiszen E,A,B egy c oldalú szabályos háromszöget határoz meg, ahol A és B pötty. G pötty lesz, mert E és D iksz. A H viszont, ha pötty, C-vel és G-vel, ha iksz, E-vel és F-fel határoz meg azonos színű szabályos háromszöget.
 

A tér színezései
 

Eddig a sík pontjait színeztük ki, most a kiszínezett térrel fogunk foglalkozni. Itt mindazok a kérdések feltehetők, amiket a síkban vizsgáltunk. Persze amikor a síkra kimondott tételben egy alakzat létezését igazoljuk, akkor ezzel egyben térbeni létezését is beláttuk, sőt többet, azt, hogy a tér minden síkjában létezik az alakzat.
A 3. tételben egy kérdésre negatív választ adtunk: hogy két színnel színezve a síkot, nem biztos, hogy létezik d oldalú szabályos háromszög. Térben nem így van.
 

6. Tétel: Két színnel színezve a teret, biztosan létezik d oldalú szabályos háromszög.
 

Bizonyítás. Vegyünk fel 2 azonos színű ‐ mondjuk pötty ‐ egymástól d távolságra levő pontot. Tekintsük a mindkettőtől d távolságra levő pontokat a térben, melyek egy 32d sugarú kört alkotnak. Ha ezen pontok között van 2 pötty, készen vagyunk, így a továbbiakban feltesszük, hogy a kör minden pontja iksz. Ha, ezen az iksz színű körön kiválasztunk két pontot, melyek távolsága d, akkor hasonló módon feltehetjük, hogy az ezektől d távolságra levő pontok alkotta kör minden pontja pötty. Így a kör minden d távolságú pontpárjához tartozik egy pötty színű kör, amelyek együttesen egy pötty színű tóruszfelületet alkotnak. Ha a tórusz adatait kiszámoljuk, kiderül, hogy a sugara 3+23d. (Kiderül mellesleg az is, hogy ez egy önmagába metsző tórusz, tehát középen nem lyukas.) Mivel a tórusz sugara 3+22d nagyobb, mint a d oldalú szabályos háromszög körülírt körének sugara, 13d, azért az is rögtön látszik, hogy a tórusz felületén lehet találni (végtelen sok), a d oldalú szabályos háromszög csúcsainak megfelelő ponthármast, amelyik tehát iksz színű.
Az 5. és 6. Tételből egyszerűen következik az alábbi
 

7. Tétel: A teret három színnel színezve, ott tetszőleges háromszög előfordul.
Térjünk most vissza átmenetileg a síkhoz. Az 1. Tételben kimondtuk, hogy két színnel színezve a síkot, tetszőleges d-hez találunk két azonos színű pontot, melyek távolsága d. Előfordulhat, hogy mindkét színben létezik minden távolság, de az is lehet, hogy van olyan távolság, ami csak az egyik színben szerepel. Erre az esetre vonatkozik a következő két tétel.
 

8. Tétel: Ha van olyan távolság, ami az egyik színben szerepel, akkor a másik színben tetszőleges háromszög létezik.
 

Bizonyítás: Ha például nem létezik két iksz színű, egymástól d távolságra levő pont, akkor be fogjuk látni, hogy a pötty színben minden háromszög létezik. A háromszöget jellemezze most az egyik csúcsából a másik két csúcsába mutató vektor, a és b. Vegyünk fel egy olyan alakzatot, amilyennel a 2. tételnél és az 1. ábrán találkoztunk, és ‐ legyen itt az ezt meghatározó távolság a d. Könnyen ellenőrizhető a következő állítás: az alakzatban szereplő 7 pont közül legfeljebb 2 lehet iksz színű, mert már három pont között biztosan van kettő, melyek távolsága d ‐ amit viszont kezdeti feltevésünkben kizártunk. Toljuk most el az egész alakzatot, az a és a b vektorral ! (6. ábra). A megfelelő pontok ekkor 7, az eredetileg felvett háromszöggel egybevágó háromszöget határoznak meg. Miután a 21 pont közül a fentiek miatt legfeljebb 6 iksz színű pont van, a 7 egybevágó háromszög között biztosan van legalább egy olyan, amelyiknek minden pontja pötty színű. Ezzel be is láttuk az állítást.
 
 
6. ábra
 

Nemrégiben jelent meg a következő két eredmény: egyrészt az előbbi tétel négyszögekre is igaz, tehát ha van olyan távolság, ami az egyik színben nem szerepel, akkor a másik színben tetszőleges négyszög létezik. Másrészt viszont a tétel tizenkétszögre (és ennél több-szögre) nem igaz, vagyis megadható olyan színezés és olyan tizenkétszög, hogy az egyik színben nem szerepel minden távolság, és a másik színben nem létezik a tizenkétszög. (E tételek bizonyítása bonyolultabb.) 4<n<12 esetben a probléma megoldatlan.
 

9. Tétel:Ha van olyan d távolság, ami az egyik színben nem szerepel, akkor a másik színben létezik 4, egy egyenesbe eső pont, melyek közül a szomszédosak távolsága 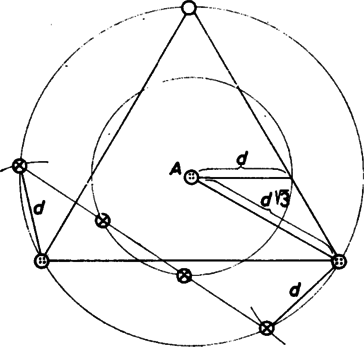d.
 
 
7. ábra
 

Bizonyítás: Ha például a pötty színben nem létezik a d távolság, akkor a pötty színű A ponttól d távolságra levő pontok ‐ az A középpontú, d sugarú kör pontjai ‐ iksz színűek. A d sugarú kör a vele koncentrikus 3d sugarú körbe írt szabályos háromszög oldalait harmadolja ‐ ez rövid számolással belátható ‐, és a harmadoló pontok távolsága d (7. ábra). Tehát ha a szabályos háromszög csúcsai között van két iksz, akkor máris megvan a keresett négy pont. Ezért feltehetjük, hogy legfeljebb 1 iksz színű, tehát legalább két pötty színű csúcsa van a szabályos háromszögnek. Jelöljünk ki a 3d sugarú körön egy-egy olyan pontot, amely a pötty színű csúcstól d távolságra van, azonos forgásirányban (ezt kétféleképp tehetjük). Ez a két pont az eredeti feltétel szerint csak iksz lehet. Az ezek által meghatározott húr másrészt felfogható úgy, mint a pötty színű csúcsok által meghatározott húr elforgatottja ‐ tehát ugyanolyan hosszú. Következésképpen a belső kör ezt a húrt is harmadolja, a harmadolópontok szintén iksz színűek, tehát megvan a 4 iksz színű pont.
 

10. Tétel: A teret két színnel színezve vagy az egyik színben (pötty) létezik d szárú egyenlő szárú derékszögű háromszög, vagy a másik színben (iksz) létezik d oldalú négyzet.
 

Bizonyítás: Ha a pötty színben nem létezik a d távolság, akkor egy pötty színű pont köré írt d sugarú gömb minden pontja iksz színű. Egy ilyen gömbre ráírható d oldalú négyzet ‐ azaz kiválasztható négy pont a gömb felületén úgy, hogy ezek d oldalú négyzetet határozzanak meg, amely tehát iksz színű.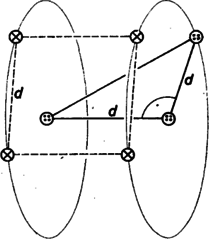
 
 
8. ábra
 

Ha a pötty színben létezik a d távolság (8. ábra), akkor a két pötty színű, pont köré írt, a d szakaszra merőleges síkú, d sugarú körökön vagy van pötty színű pont, és akkor d szárú egyenlő szárú derékszögű háromszöget találtunk, vagy a körökön minden pont iksz színű, akkor található 4 pont, melyek d oldalú négyzetet határoznak meg. (Persze a két alakzat egyszerre is létezhet.)
 

Végezetül az esetleges további érdeklődőknek ‐ és angolul tudóknak ‐ megadjuk azt a négy cikket, mely forrásunkul szolgált, és amely az itt leírtaknál jóval többet tartalmaz.
 

P. Erdős, R. L. Graham, P. Montgomery, B. L. Roth, J. Spencer, E. G. Straus: Euclidean Ramsey Theorems I. Journal of Combinatorial Theory, Series A, 14 (1973), 341‐363. o.
     Euclidean Ramsey Theorems II, III. Infinite and Finite Sets, Coll. Math. Soc. J. Bolyai Vol. (1969) 529‐585. o.
Rozália Juhász: Ramsey Type Theorems in the Plane, Journal of Combinatorial Theory, Series A, 27, Number 2, Sept. 1979, 151‐161.o.