|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Vegyünk egy szabályos -szöget, és tükrözzük az oldalaira. Ha , az új sokszögek még nem érnek össze, forgassuk ki őket a térbe addig, amíg nem találkoznak. Ha , egy zárt hálózatot kapunk, a négylapú test neve tetraéder. Ha , a szabadon maradó élek egy hatodik négyzetet határoznak meg, és a lapok ezzel együtt egy kockát határolnak. Ha , összesen él marad szabadon (minden lapon kettő) és belőlük szeszélyes térbeli vonal alakul ki. Ha azonban ebben összekötjük a szemközti csúcsokat, egymást egy pontban metsző egyeneseket kapunk. Erre tükrözve a vonalat, az önmagába megy át, így a hat ötszögből álló rendszer tükörképe folyamatosan csatlakozik az eredeti rendszerhez, és azzal együtt egy lapú szabályos testet határoz meg, amit dodekaédernek nevezünk (1. ábra).
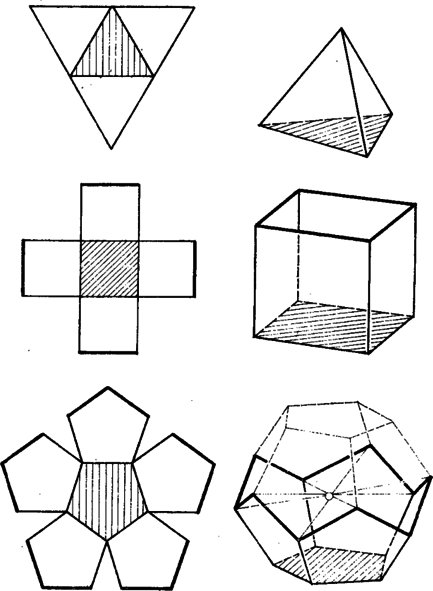 1. ábra
Centruma van természetesen a kockának is, és a tetraéder csúcsain átmenő gömb középpontját is tekinthetjük a tetraéder középpontjának. A lapok középpontjai mindhárom testen egy-egy újabb gömbön helyezkednek el, melyek a csúcsokon átmenő gömbökkel koncentrikusak. A közös csúcsú lapok centrumaiból egy-egy újabb szabályos sokszög csúcsai állíthatók össze, és mivel egy-egy csúcsban mindhárom testen három lap találkozik, ezek mind szabályos háromszögek. A lapközéppontok tehát olyan testek csúcsai, amelyek minden lapja szabályos háromszög. A lapok száma különben egyenlő a kiindulásul vett test csúcsainak a számával, vagyis rendre , , , a megfelelő testek neve tetraéder, oktaéder, ikozaéder.
A kapott öt szabályos test tetraéder-tetraéder, oktaéder-kocka, ikozaéder-dodekaéder párbaállítását igazolja az is, hogy e párokban az élfelezőpontok azonos (pontosabban mondva egymáshoz hasonló) testeket határoznak meg. 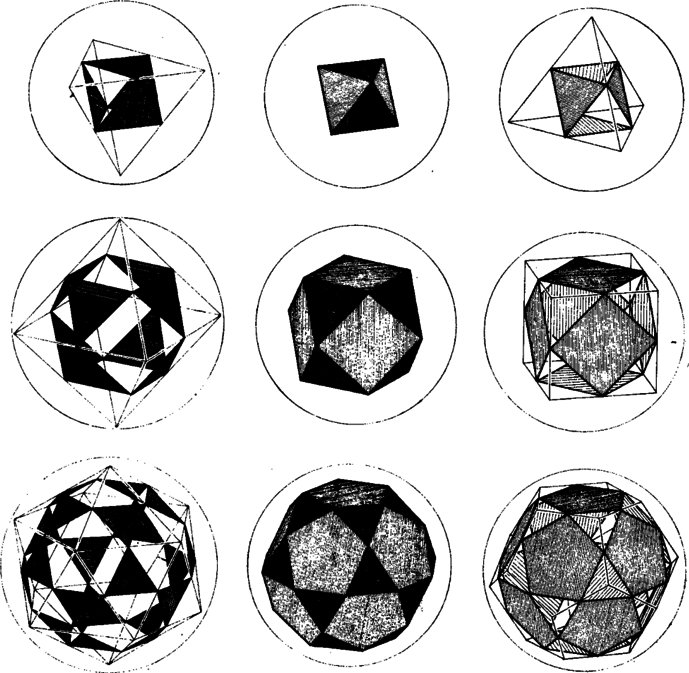 2. ábra
Mivel az élek mind egy-egy gömb egyenlő hosszúságú húrjai, felezőpontjaik ismét egy, az eredeti gömbbel koncentrikus gömbön vannak. Az élfelezőpontok által meghatározott test lapjai között azonban a pár mindkét tagjának a lapjai megtalálhatóak, így az új test csak mellett lesz ismét szabályos, amikor is az oktaédert kapjuk. A másik két esetben a lapok között a háromszögek négyszögekkel, illetve ötszögekkel váltakoznak, az ilyen testeket félig szabályosaknak mondjuk (2. ábra).
Az élfelező pontok által meghatározott testet úgy is megkapjuk az eredeti testekből, ha az egy csúcsban találkozó fél-élek által meghatározott gúlákat levágjuk róluk. Mi történik, ha kisebb gúlákat vágunk le ? A visszamaradó testben e gúlák alapsokszögei továbbra is szabályosak lesznek, hiszen a felezéskor keletkező lapok kicsinyített másai, de az eredeti testek oldallapjaiból általában nem szabályos sokszög marad vissza. Ha ugyanis egy szabályos -szögből a csúcsokkal együtt egybevágó, egymásba nem nyúló háromszögeket vágunk le, olyan oldalú sokszög marad vissza, amelyik akkor és csakis akkor szabályos, ha a levágott háromszögek alapjai az eredetivel egybevágó sokszöget alkotnak (3. ábra). Vágjunk hát le a testekből szabályos -szögeket meghatározó gúlákat, újabb félig szabályos testeket kapunk. (A csúcsok ilyen szabályos gúlakörnyezetének vagy a szabályos lapok alatti csonkagúlák eltávolítását, levágását csonkításnak nevezzük.)
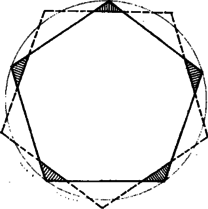 3. ábra
Az eddig előállított testek láthatóak a 4. ábra középső öt oszlopának első három sorában. A testek alá a csúcsaikban találkozó sokszögek oldalszámát írtuk. A negyedik sor a cikket indító gondolat melletti végrehajtásából származik, a sokszögek most az eredeti sokszög síkjában csatlakoznak egymáshoz. A térben végrehajtott lépések azonban némi fantáziával az így kapott, az egész sík lefedésére szolgáló mozaikon is végrehajthatóak, és újabb mozaikokra vezetnek. Ha , a sokszögek már egymásba nyúlnak, de a már vizsgált esetben a kapott négyzetlapokat eredeti síkjukban hagyva belőlük mozaikot is kaphatunk, ez és származékai találhatók táblázatunk utolsó sorában.
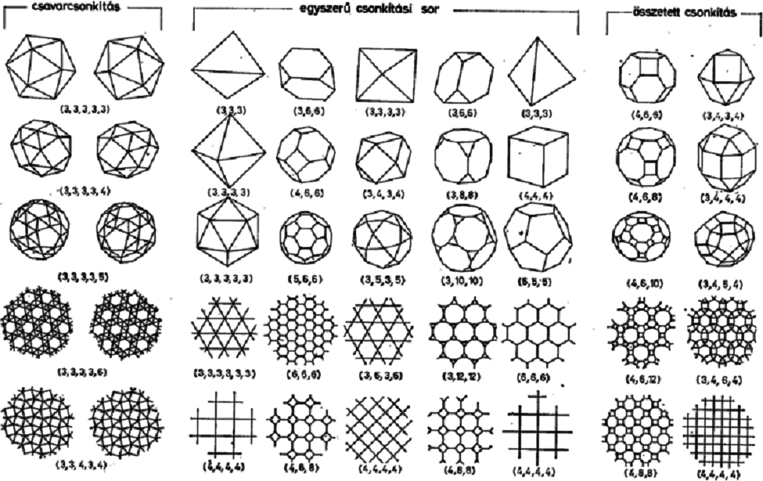 4. ábra
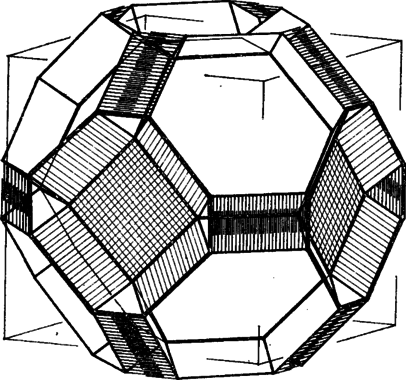 5. ábra
Térjünk vissza a már meghatározott szabályos és félig szabályos testekre. Alakítsuk tovább az utolsó lépésben kapott testeket. Ezek közös tulajdonsága, hogy határoló lapjaik között egymáshoz csatlakozó magas (, vagy ) oldalszámú sokszögek egy-egy alacsony (, vagy ) oldalszámú sokszöget fognak közre. Helyezzünk ezekre a lapokra egy-egy nem túl magas hasábot. A csatlakozó élek így megkettőződnek, általában egy-egy téglalapot határoznak meg, amelyek négyzetekké lesznek, ha a hasábok magasságát alkalmasan választjuk meg (5. ábra). Ezzel egyidejűleg az alacsony oldalszámú sokszögekből egy-egy kétszeres oldalszámú szabályos sokszög keletkezik. Így kapjuk a jobb oldali két oszlop közül az elsőt, az utolsó oszlop pedig a középső oszlopból származtatható, ennek részletezését az olvasóra hagyjuk. Ugyancsak a középső oszlop testjeiből származtathatóak a bal oldali két oszlopban található testek. Mozgassuk el e testek , , illetve oldalú lapjait a testtől bizonyos távolságra, és közben enyhén forgassuk el mindegyiket. Eredetileg egymásba fogódzó csúcsaik egy idő után a szomszédos lapok élfelező pontjaival találják szemben magukat, és ha elég ügyesek vagyunk, azokkal egy-egy szabályos háromszöget határoznak meg.
Joggal vethető fel a kérdés, hol a határ, hány újabb és újabb trükk van még, amelyek esetleg további félig szabályos testekre vezethetnek. Két követelmény van csak, a lapok szabályossága és a csúcsok egybevágósága, az utóbbin a csúcsokban összefutó élek merev rendszerének az egybevágóságát értve. Ennek vizsgálatát is az olvasóra hagyjuk, de annyit elárulunk, hogy a táblázatunk bizonyos értelemben teljes, ami belőle kimaradt, az már egyszerűen áttekinthető. Érdemes megjegyezni azonban, hogy a 4. ábra minden félig szabályos testje (vagy mozaikja) előállítható a sorában található szabályos test előbb bemutatott csonkításával (mozaikoknál a csonkításon a csúcs körüli szabályos sokszögkörnyezetek kiemelését értve).
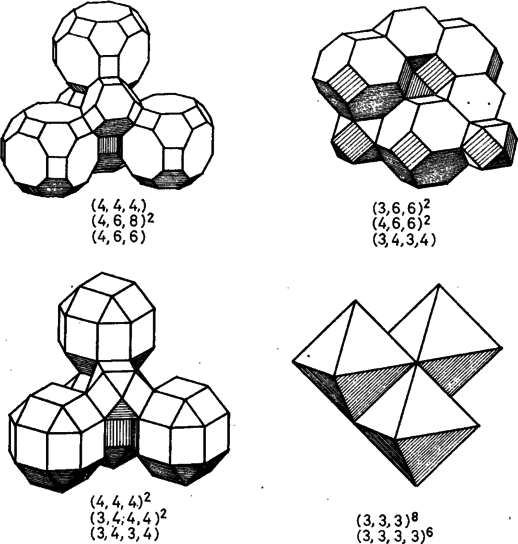 6. ábra Ugyancsak az olvasóra hagyjuk a 6. és 7. ábra értelmezését, melyek az egyetlen térbeli szabályos mozaik csonkolásával származtatják le a tér félig szabályos testekből felépíthető összes ,,kitapétázását''. Amennyiben olvasóink a módszer továbbfejlesztéséről érdeklődnek, folytathatjuk a 4 dimenziós testek elrendezésével is. 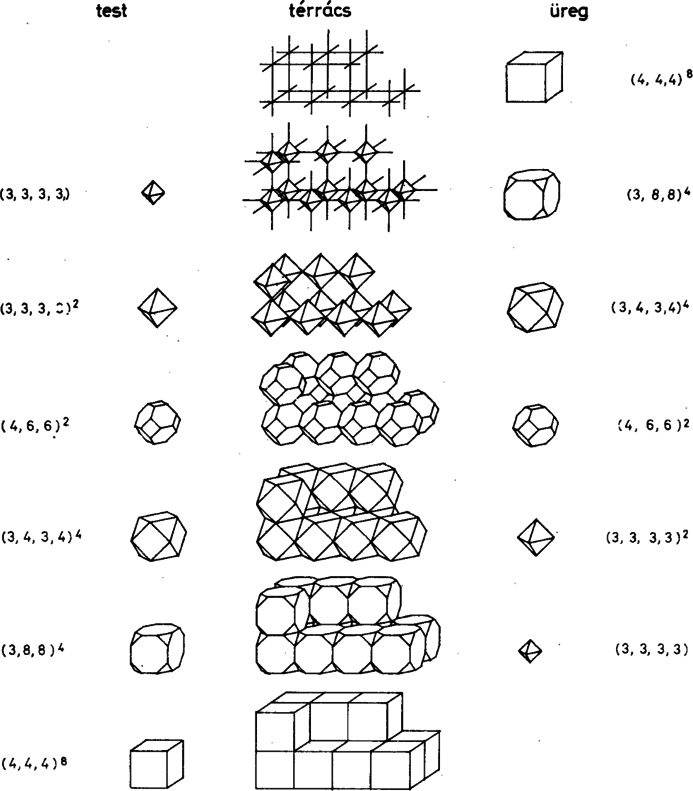 7. ábra Az érdeklődő olvasónak a következő könyveket ajánljuk:
A cikkben közölt állítások bizonyítását az olvasóra hagyjuk. Minden, ezekkel foglalkozó írást érdeklődéssel várunk. ‐ A szerkesztőség. |
 PDF | MathML
PDF | MathML