Cím: Mozoghat-e valaki, akit síklapokkal határolt páncélba öltöztettünk?
Szerző(k):  Csirmaz László 
Füzet: 1979/november, 119 - 123. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Töprengett-e már az olvasó azon, hogy amikor egy poliédert (sokszöglapokkal határolt testet) hálózatával* definiálunk, megadjuk-e ezzel egyáltalán a testet?

 

 
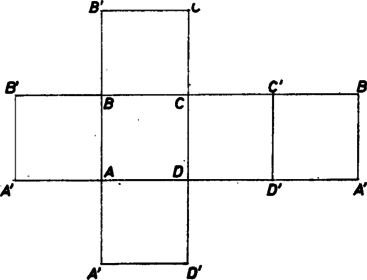1. ábra

Az 1. ábrán látható hálózatból csak egyetlen test állítható össze, a kocka. Ugyanakkor a 2. ábra hálózatából már három különböző poliéder is összeállítható: egy konvex és két konkáv (3. ábra). Ez a példa is mutatja, hogy a hálózat általában nem definiálja egyértelműen a poliédert, az összeillesztésnél több különböző lehetőségünk van, bár az egy csúcsban összefutó lapok, és azok sorrendje adott. De az összerakott (összeragasztott) lapokból keletkező testek már merevek: ha modelljeinkben bármelyik három csúcsot rögzítjük, semelyik további csúcs nem mozoghat. Ahhoz, hogy a konkáv testek ,,horpadásait'' kipattinthassuk, már a papír rugalmasságát kell kihasználnunk. A pattintás közben az oldallapok átmenetileg megszűnnek síklapok lenni. Merevségen tehát azt értjük, hogy amennyiben a poliéder lapjai adott síklapok, és bár ezek a lapok csuklósan vannak az élek mentén összeillesztve, azaz a lapok az élek körül szabadon elfordulhatnának, a poliéder csúcsait mégsem tudjuk egymáshoz képest mozgatni.
 

 
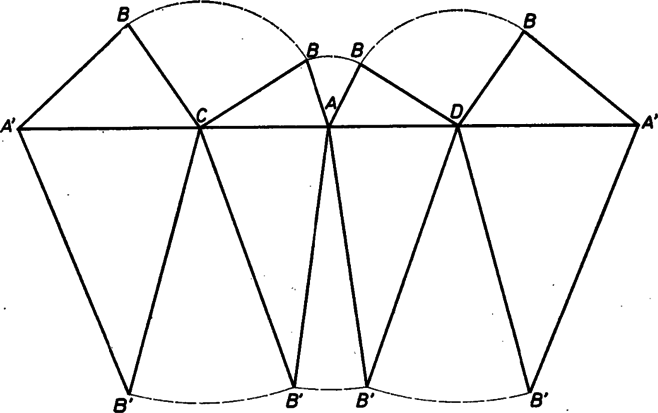2. ábra
 

 
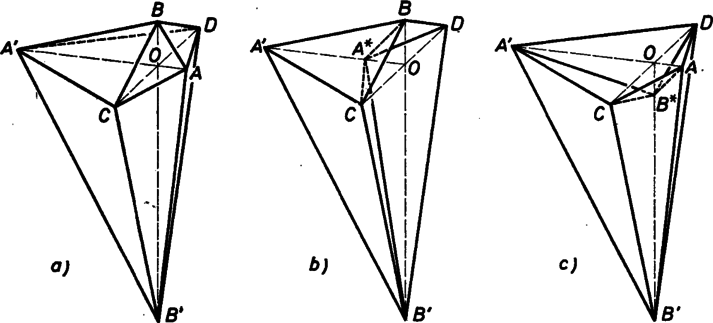3. ábra

 

Az előbbi definíciónak síkbeli megfelelője az lehetne, hogy egy sokszög akkor merev, ha oldalszakaszai a csúcsokban csuklósan találkoznak és a sokszög csúcsainak a kölcsönös helyzete ennek ellenére nem változtatható meg. Eszerint a háromszög volna az egyetlen síkbeli merev sokszög. Ennek fényében még inkább meglepő a poliéderek tapasztalt merevsége. Hátha csak bizonyos ,,szép'' tulajdonságú poliéderek merevek, a legtöbbjük pedig nem az? Nos, Augustin-Louis Cauchy (1789‐1857) neves francia matematikus 1813-ban bizonyította, hogy minden konvex poliéder merev. Sőt ennél többet mutatott meg, nevezetesen azt, hogy adott hálózatból legfeljebb egy test állítható össze. Így a 2. ábra hálózatából is csak egyetlen konvex poliédert kaphatunk (3a ábra), míg konkávból már kettőt (3b, c ábrák). Az állítás bizonyítása megtalálható például Skljarszkij ‐ Csencov ‐ Jaglom: Válogatott feladatok, 3., Geometria II. (Sztereometria) című könyvének 58. feladatában.

 

 
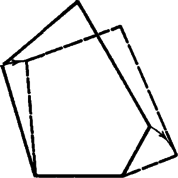4. ábra

 

 
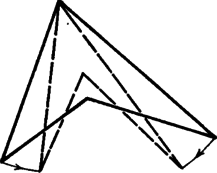5. ábra

 

Több mint másfél évszázadon keresztül próbálták Cauchynak ezt a tételét konkáv poliéderekre is átvinni, vagy pedig ellenpéldát keresni. Cauchy tételének bizonyítása azon a tényen alapszik, hogy ha egy konvex sokszöget az oldalhosszak megtartásával úgy deformálunk, hogy továbbra is konvex maradjon (4. ábra), akkor legalább 2 szöge csökken és legalább 2 szöge nő. Ez azonban konkáv sokszögekre már nem marad érvényben, például az 5. ábrán a három hegyesszög csökkent és csak a konkáv szög nőtt. Ez az oka annak, hogy a bizonyítást nem lehetett konkáv poliéderekre is átvinni. Végül 1978-ban Robert Connelly konstruált egy nem merev konkáv poliédert. A továbbiakban egy ilyen, csupa háromszöglapokkal határolt testet írunk le. Ezt a testet Klaus Steffen találta meg.
 

 
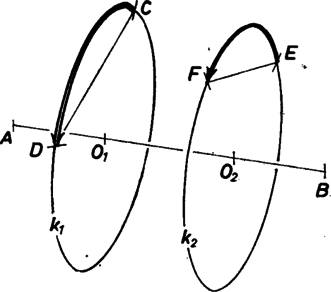6. ábra

 

Tekintsünk a térben két pontot, A-t és B-t. Azon pontok mértani helye, melyek A-tól adott a, B-től pedig b távolságra vannak, egy k1 körvonal, ha a+b>AB. Ennek síkja merőleges az AB egyenesre (6. ábra). Hasonlóan legyen k2 az a körvonal, melynek pontjai A-tól b, B-től pedig a távolságra vannak. Világos, hogy k1 és k2 egybevágóak és az AB szakasz felezőpontjára tükrösek. Válasszunk ki a k1 körvonalon két pontot, C-t és D-t, a k2 körvonalon pedig válasszuk az E és F pontokat úgy, hogy a CD ív és az EF ív egyenlő és egyező körüljárású legyen. Ezt úgy értjük, hogy az AB tengely valamelyik irányából nézve (a végtelenből) ugyanakkora és egyező irányú elforgatás vigye át C-t a D-be és E-t az F-be (7. ábra). Ekkor a CD és EF szakaszok egyenlőek, sőt a CE és DF szakaszok is, hiszen az ACEB töröttvonalat az AB tengely körül alkalmas szöggel elforgatva az ADFB töröttvonalat kapjuk.
 

 
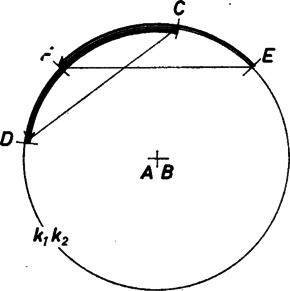7. ábra

 

Így ha az AC, CB, AD, DB, AE, EB, AF, FB, CD, EF és CE szakaszok helyére merev rudakat teszünk (ez összesen 11 rúd), a rudak végpontjait csuklókkal illesztjük össze, az A és B pontokat bizonyos korlátok között közelíthetjük, illetve távolíthatjuk egymástól. A-t és B-t távolítva k1 és k2 átmérője csökken, és csökken a síkjaik közti távolság is. A fix CE rúd miatt nő az elfordulás CD és EF között (8., 9. ábra). Eközben a fenti meggondolás alapján a DF távolság nem változik, így a D és F pontok közé is illeszthetünk egy rudat, a rendszer mozgathatósága megmarad. A mozgathatóságot úgy is gondolhatjuk, hogy az A, E, F pontokat rögzítve a B pontot fel-le mozgathatjuk (10. ábra).
 

 
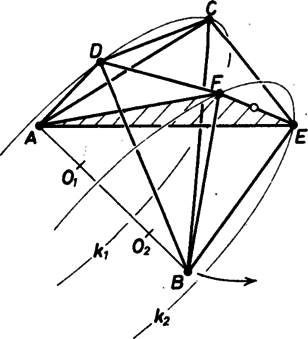8. ábra

 

 
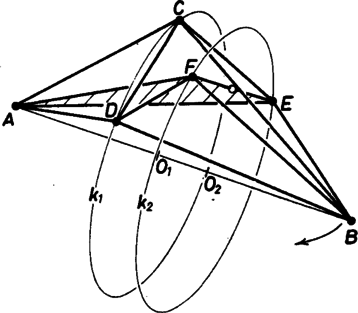9. ábra

 

 
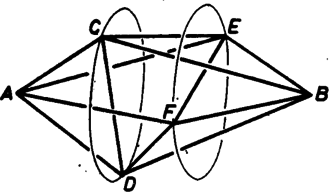10. ábra

 

A rudak méreteinek ügyes megválasztásával elérhetjük, hogy az ACE, ACD, ADF, BEC, BDC, BDF háromszöglapokat feltéve a csuklós rendszerünkre (11. ábra) egy, az AEBF torz négyszögre illeszkedő nyitott felületet kapjunk. Például a=10cm, b=12cm, CD=11cm és CE=5cm megfelelő lesz. Minthogy a háromszöglapok oldalszakaszai az előbbi csuklós rendszer rúdjai közül kerülnek ki, ez a felület is olyan marad, hogy az A, E, F pontokat rögzítve a B pont fel és le mozgatható, a lapok alakváltozás nélkül követik a B pont mozgását.
 

 
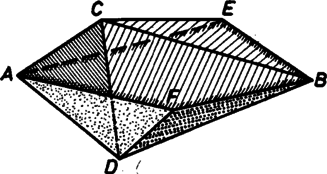11. ábra

 

Készítsük el két példányban ezt a felületet. Helyezzük egymásra azokat és ragasszuk össze a két felületet a BE, valamint BF élek mentén. Ezután az A csúcsnál óvatosan húzzuk szét. Az ,,alap'' ABCDEF felett kapunk egy A'BC'D'EF ,,fedőlapot''. Amíg az A és A' csúcsok távolsága kb. 10cm-nél kisebb, addig a BCD és BC'D' lapok összesimulnak és a testet merevvé teszik. Ha azonban ez a távolság úgy 15-16cm-re nő, az alap- és a fedőlap szabaddá, egymáshoz képest mozgathatóvá válik. A keletkezett AA'E és AA'F háromszöglapokat beragasztva (válasszuk AA'-t 16cm-nek) máris előttünk áll egy nem merev poliéder. Ennek 9 csúcsa, 14 lapja (mindegyik háromszöglap) és 21 éle van. Ha rögzítjük az A, A', E és F csúcsokat, akkor a B csúcsot folytonosan mozgathatjuk (addig, amíg a poliéder lapjai össze nem akadnak), hiszen a végén beillesztett AA'E és AA'F lapok változatlanok, a poliéder alsó és felső ,,kosara'' pedig külön-külön, tehát egyszerre is mozgatható.
Hátsó borítónkon a test teljes hálózata látható, nagyjából feleakkora méretben, mint amekkorát megadtunk. A felületre írt számok az összeragasztás sorrendjét jelzik. A vastagon kihúzott élek mentén a lapszögek konkávak, azokat az ellenkező irányba kell behajtani, mint a többi élt.
 Csirmaz László
 

 
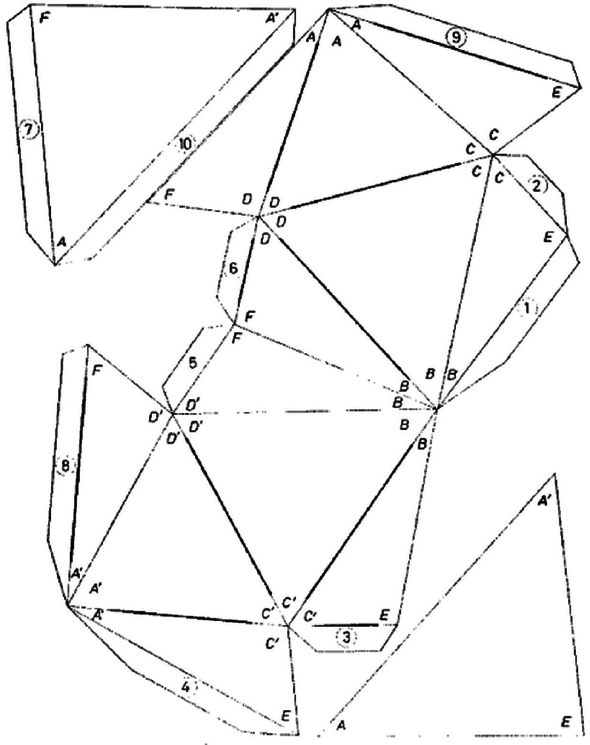A hátsó borító ábrája
*A hálózat helyett a lapgráf kifejezést kellene használnunk, hiszen nem csupán a poliéder síkba kiterített lapjait gondoljuk megadottnak, hanem azt is, hogy a lapok hogyan csatlakoznak egymáshoz. Ennek ellenére megmaradunk a szemléletesebb hálózat kifejezésnél.