Kezdőlap


Cím:	Kalkulátor problémák
Szerző(k):	Lukács Ottó
Füzet:	1979/november, 114 - 119. oldal	PDF \| MathML
Témakör(ök):	Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Be nem épített függvények

Van egy zsebszámítógépem, HT TK ‐ 1024 a neve, magyar gyártmány. Sok mindent tud: leütöm az

x

-et, egy-egy billentyű benyomására kiszámítja

x^{2}

-et,

\sqrt[]{x}

-et,

sin - cos - tg x

-et,

\frac{1}{x}

-et stb. Egy billentyű benyomására megjelenik a

π

értéke

9

tizedes jegyre kerekítve, tud összeadni‐kivonni‐szorozni‐osztani.
Ezenkívül a

sin

cos

tg

szögfüggvények adott értékéből a szögek meghatározása is egy-egy gomb megnyomásával történhet. Adott szögfüggvényértékhez végtelen sok különböző szög tartozik, a kalkulátor azonban csak egyetlen értéket tud kijelezni. Ez az érték az ún. főérték, szokásos jele és értékkészlete

\begin{matrix} - \frac{π}{2} & \leq Arc sin x \leq \frac{π}{2} \\ 0 & \leq Arc cos x \leq π \\ - \frac{π}{2} & < Arc tg x < \frac{π}{2} . \end{matrix}

Így például a

tg x = 1

értékből a gép egyedül az

x = 0, 78 ...

szöget keresi vissza, ebből nekünk kell a többi szögértéket meghatároznunk:

x \approx 0, 78 + k π

, ahol

k

tetszőleges egész.
Sajnos, a kalkulátorban nincs

Arc ctg x

-et számító szubrutin, adott

ctg x

értékből

x

-et nem lehet közvetlenül visszakeresni. Pedig a gyakorlatban erre is szükség lehet.
Ha rövid a kardod, toldd meg egy lépéssel ‐ tartja a közmondás. Hogyan lehetne az eddig felsorolt szubrutinok segítségével adott

ctg x = a

értékből

x

főértékét,

Arc tg a

-t meghatározni? Definíció szerint a főérték

0

és

π

közti érték:

\begin{matrix} 0 < Arc ctg x < π . \end{matrix}

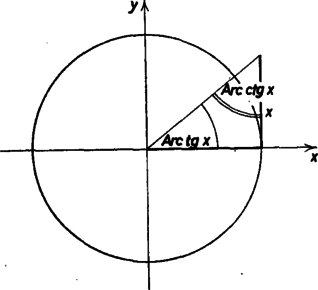1. ábra

I. Gondoljuk végig: az egységsugarú, origó középpontú körben

Arc tg x

azt a szöget jelenti, amelynek a tangense

x

(ez az 1. ábrán az egyíves szög).

Arc ctg x

azt a szöget jelenti, amelynek a cotangense

x

(ez az 1. ábrán a kétíves szög). Ha

0 < Arc tg x < \frac{π}{2}

, a két szög egy derékszögű háromszög két hegyesszöge, ezek összege tehát

\frac{π}{2}

\begin{matrix} Arc tg x + Arc ctg x = \frac{π}{2} . \end{matrix}

Érvényes-e ez negatív szögre is? Igen, mert

tg (- x) = - tg x

| Arc tg x | < \frac{π}{2}

miatt

\begin{matrix} Arc tg (- x) = - Arc tg x \end{matrix}

(lásd a 2. ábrát), és

ctg (π - x) = - ctg x

0 < Arc ctg x < π

miatt

\begin{matrix} Arc ctg (- x) = π - Arc ctg x \end{matrix}

(lásd a 3. ábrát).

2. ábra

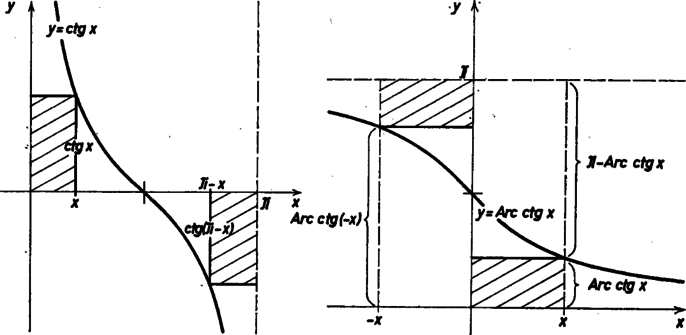3. ábra

A két utóbbi egyenlőséget összeadva és rendezve azt kapjuk, hogy

\begin{matrix} Arc ctg x = \frac{π}{2} - Arc tg x, \end{matrix}

ez az összefüggés tehát érvényes minden

x

-re.
Így ez módot ad arra, hogy a kalkulátor meglevő szubrutinjaival adott

ctg x

értékből

x

-et visszakeressük. Például:

\begin{matrix} ctg x = 0, 5 x = Arc ctg 0, 5 + k \cdot π = \frac{π}{2} - Arc tg 0, 5 + k π \approx 1, 107 148 718 + k π . \end{matrix}

II. Készítsünk egy másik módszert is, más szubrutinok bevonásával.
Ha

x > 0

, akkor

0 < Arc ctg x < \frac{π}{2}

és

\begin{matrix} tg (Arc ctg x) = \frac{1}{ctg (Arc ctg x)} = \frac{1}{x} . \end{matrix}

Ha egy

0

és

\frac{π}{2}

közti szám tangense

\frac{1}{x}

, akkor az a szám

Arc tg \frac{1}{x}

-szel egyenlő:

\begin{matrix} Arc ctg x = Arc tg \frac{1}{x}, ha x > 0. \end{matrix}

x < 0

, akkor

\frac{π}{2} < Arc ctg x < π

, de most is

\begin{matrix} tg (Arc ctg x) = \frac{1}{ctg (Arc ctg x)} = \frac{1}{x} . \end{matrix}

Ebből

Arc ctg x = Arc tg \frac{1}{x} + k π

következik, ahol

k = 1

, hiszen most

- \frac{π}{2} < Arc tg \frac{1}{x} < 0

\frac{π}{2} < Arc ctg x < π

. Tehát

\begin{matrix} Arc ctg x = Arc tg \frac{1}{x} + π, ha x < 0. \end{matrix}

Ezek az eredmények azt mutatják, hogy

Arc ctg x

értékét az

\frac{1}{x}

, az

Arc tg

, a

π

és az összeadó szubrutinok segítségével is meghatározhatjuk. Például:

\begin{matrix} ctg x & = - 0, 35, \\ x & = Arc ctg (- 0, 35) + k π = Arc tg (- \frac{1}{0, 35}) + (k + 1) π \approx \\ \approx & - 1, 234 121 507 + (k + 1) π . \end{matrix}

2. Egyenletek megoldása

Játsszunk egy kicsit a kalkulátorral. Vigyünk be

1

radiánt és vegyük ennek a cosinusát. A kapott értéknek is vegyük a cosinusát, majd az így kapott értéknek is számítsuk ki a cosinusát és így tovább. A cos-gomb nyomogatásával az alábbi számsorozatot kaptuk:

\begin{matrix} Sorszám & x_{i} & cos x_{i} \\ 1. & 1, & 0,540 302 3059 \\ 2. & 0,540 302 3059 & 0,857 553 2158 \\ 3. & 0,857 553 2158 & 0,654 289 7905 \\ 4. & 0,654 289 7905 & 0,793 480 3587 \\ ... & ... & ... \\ 58. & 0,739 085 1333 & 0,739 085 1332 \\ 59. & 0,739 085 1332 & 0,739 085 1332 \end{matrix}

Így voltaképpen adott

x_{i}

értékből

cos x_{i}

-t számoltuk ki, azután az

x_{i + 1} = cos x_{i}

értékből

cos x_{i + 1}

-et (

i = 1

2

3

...

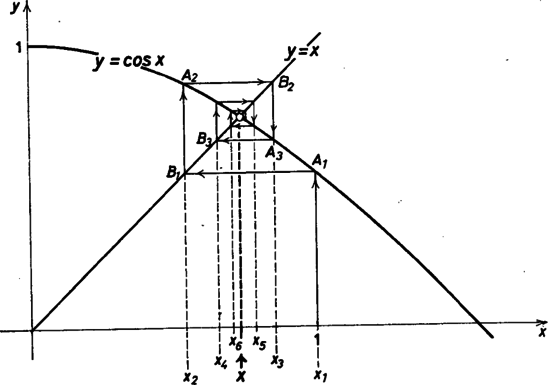4. ábra

A 4. ábra vázlatosan mutatja eljárásunkat. Először az

y = cos x

görbén megkeressük az

A_{1} (x_{1}; cos x_{1})

pontot, ezt az

x

tengellyel párhuzamosan rávetítjük az

y = x

egyenesen levő

B_{1}

pontra, ezt fölvetítjük

y

tengellyel párhuzamosan a

cos x

görbén levő

A_{2} (x_{2}; cos x_{2})

pontra, és így tovább. Az

A_{1} B_{1} A_{2} B_{2} A_{3} B_{3} ...

töröttvonal fokozatosan egy pontot közelít meg, az

y = cos x

és

y = x

metszéspontját.

Az eljárással (úgynevezett ,,iteráció''-val) az

\begin{matrix} x = cos x \end{matrix}

egyenlet megoldását határoztuk meg egyre pontosabban. Az

x_{1}

x_{2}

x_{3}

...

abszcissza-sorozat egyre nagyobb pontossággal közelíti meg az

x = cos x

egyenlet gyökét.
Az 59. lépésben kapott

x_{59}

a gép tanúsága szerint már megegyezik

cos x_{59}

-cel, ezzel a kalkulátorral tehát az eljárás nem javít tovább a gyök pontosságán, az

x = cos x

egyenlet megoldása

\begin{matrix} x \approx 0, 739 085 133 2. \end{matrix}

Az eljárást alkalmazhatjuk más

\begin{matrix} x = φ (x) \end{matrix}

alakú egyenletek megoldására is. A kapott sorozat egyre nagyobb pontossággal megközelíti az egyenlet gyökét, ha a

φ (x)

,,elég laposan'' metszi át az

y = x

egyenest, pontosabban: ha az érintőjének iránytangense,

φ' (x)

abszolút értékben kisebb

1

-nél a gyökhely környezetében:

\begin{matrix} | φ' (x) | < 1, \end{matrix}

azaz a gyökhely környezetében az érintő hajlásszöge

- 45^{\circ}

és

+ 45^{\circ}

között mozog (5a, b ábra). Az eljárás nem vezet a gyökhöz, ha

| φ' (x) | > 1

, (5c, d ábra).

5. ábra

Mit tehetünk, ha

| φ' (x) | > 1

? A 6. ábra mutatja, hogy az

y = φ (x)

és inverze,

y = φ^{- 1} (x)

ugyanazon pontban metszik az

y = x

egyenest (persze, mert egyik a másiknak tükörképe az

y = x

egyenesre). Ha

| φ' (x) | > 1

, akkor

| [φ^{- 1} (x)]' | < 1

lesz a gyökhely környezetében. Így az iterációval az

x = φ (x)

egyenlet helyett az

x = φ^{- 1} (x)

egyenletet oldhatjuk meg.

6. ábra

Nézzük például az

x + ln x = 0

egyenletet. (Itt

ln x

természetes logaritmus,

e

alapú logaritmus.)
Az

x = - ln x

helyett (mivel

- ln x

deriváltja abszolút értékben

| - \frac{1}{x} | > 1

0

és

1

közt keresendő gyökhely környezetében) az

x = e^{- x}

egyenletből érdemes kiindulnunk. Itt az

e^{x}

\frac{1}{x}

szubrutinok felhasználásával számíthatjuk ki a szükséges értékeket.

\begin{matrix} x & e^{x} & \frac{1}{e^{x}} \\ 1. & 0,5 & 1,648 721 271 & 0,606 530 659 7 \\ 2. & 0,606 530 659 7 & ... & 0,545 239 211 9 \\ 3. & 0,545 239 211 9 & ... & 0,579 703 094 9 \\ 4. & ... & ... & 0,560 064 627 9 \\ 5. & ... & ... & 0,571 172 149 0 \\ 6. & ... & ... & 0,564 862 947 0 \\ ... & ... & ... \\ 37. & 0,567 143 290 5 \\ 38. & 0,567 143 290 4 \\ 39. & 0,567 143 290 4 \end{matrix}

A kalkulátorral tovább nem javítható a gyökközelítés, az

x + ln x = 0

egyenlet gyöke

\begin{matrix} x \approx 0, 567 143 290 4. \end{matrix}

Lukács Ottó