Cím: Hány testőre volt Arthur királynak?
Szerző(k):  Csirmaz László 
Füzet: 1979/november, 97 - 101. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A tavaly szeptemberi számban kitűzött P. 306. probléma a következőképpen szólt:
,,Artúr király testőrei lovagi tornát vívtak. A torna végén kiderült, hogy a király bármely n testőrhöz tud találni egy (n+1)-ediket, aki mindegyiküket legyőzte. Bizonyítsuk be, hogy legalább 2n+1-1 résztvevő volt.''

 
 

A feladatra 5 tanuló küldött helyes megoldást: Erdélyi Tamás, Ligeti Rudolf, Lipusz Csaba, Nagy Gábor és Varga Lívia. Erdélyi Tamás dolgozatának végén megjegyzi: ,,Érdekes kérdés, hogy egy 2n+1-1 főből álló társaságra megadható-e olyan konstrukció, amelyre a feladat feltételei teljesülnek.'' Ennek az írásnak az a célja, hogy erről a kérdéskörről mindazt elmondja, amit ma a matematikusok tudnak.
Kezdjük egy definícióval. Jelölje f(n) azt a legkisebb, n-nél nagyobb egész számot, amelyre igaz a következő állítás. Ha a királynak pontosan f(n) testőre van, akkor a lovagi tornának lehetséges olyan végeredménye, hogy bármely n testőrhöz található olyan (n+1)-edik, aki mind az n-et legyőzte.
Könnyen belátható, hogy f(1)=3, az F. 2159. feladat megoldása (megjelent a Kömal 58. kötet, 1. szám 9. oldalán) szerint f(2)=7, továbbá a P. 306. probléma azt állítja, hogy f(n)≥2n+1-1. Elsőként Erdős Pál bizonyította, hogy
2n+1-1≤f(n)≤n2⋅2n+1,(1)
1965-ben azután két ausztráliai matematikus, E. és G. Szekeres megmutatták, hogy a valamivel erősebb
(n+2)2n-1-1≤f(n)(2)
egyenlőtlenség is igaz.

Elsőként (2)-t bizonyítjuk, ebből (1) első egyenlőtlensége már következik. Ehhez egy újabb definícióra van szükségünk.
Jelöljük g(n,m)-mel azt a legkisebb, n-nél nagyobb egész számot, amelyre igaz a következő állítás. Ha Artúr királynak pontosan g(n,m) testőre van, akkor a lovagi tornának lehetséges olyan kimenetele, hogy bármely n testőrt legalább m másik testőr legyőzött. Világos, hogy g(n,1)=f(n).
Legyen k=g(n,m) és tegyük fel, hogy a k testőr közötti lovagi torna végeredménye megfelel a fenti feltételnek. Nem lehetséges, hogy minden testőr több mint (k-1)/2 testőrtől kapjon ki, mert ekkor a vereségek száma több volna, mint k(k-1)/2, noha összesen legfeljebb k(k-1)/2 mérkőzés volt. Legyen tehát A olyan testőr, aki legfeljebb (k-1)/2 alkalommal kapott ki. Ha most n=1, akkor a feltétel szerint A-t legalább m testőr győzte le, azaz m≤(k-1)/2, ahonnan
g(1,m)≥2m+1.(3)

Ha n≠1, akkor állítjuk, hogy az A-t legyőző testőrök száma legalább g(n-1,m), azaz
g(n,m)≥2g(n-1,m)+1.(4)
Ehhez elegendő megmutatnunk, hogy az A-t legyőző testőrök teljesítik a g(n-1,m) definíciójában szereplő állítást.
 

 
1. ábra

 

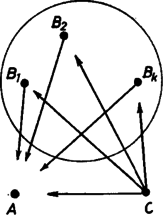Először is legalább n testőr győzte le A-t. Ugyanis ha csak a B1, B2, ..., Bk (k<n) testőrök nyertek volna A ellen, akkor az A, B1, ..., Bk testőröket tetszőlegesen kiegészítve n testőrré, volna olyan C, aki mindnyájukat legyőzte, azaz legyőzte A-t is és legyőzte B1, B2, ..., Bk-t is (1. ábra). Ez a C nem egyezhet meg egyik Bi-vel sem; és legyőzte A-t, ami ellentmond annak, hogy A-t csak B1, B2, ..., Bk győzte le. Másodszor azt kell ellenőriznünk, hogy ha a B1, B2, ..., Bn-1 testőrök mind legyőzték A-t, akkor van m testőr a legyőzők között, akik B1, B2 ..., Bn-1 mindegyikét legyőzték. Ám ezt éppen az a feltételünk biztosítja, ami szerint az A, B1, B2, ..., Bn-1 (összesen n fő) testőrhöz található m olyan testőr, akik ezt az n-et legyőzték. Ezek persze legyőzték A-t, és legyőzték B1 B2, ..., Bn-1-et is.
A (3) és (4) egyenlőtlenségek alapján teljes indukcióval bizonyítjuk, hogy
g(n,m)≥2n(m+1)-1.(5)
n=1-re az állítás (3)-mal ekvivalens. Ha n≥2 és (5)-öt már (n-1)-re tudjuk, akkor (4) szerint
g(n,m)≥2g(n-1,m)+1≥2(2n-1(m+1)-1)+1=2n(m+1)-1,
amivel a teljes indukciós bizonyításunk készen van.
 

 
2. ábra
 
Az (5) egyenlőtlenségben m=1-et téve megkapjuk (1) első egyenlőtlenségét. Ahhoz, hogy (2)-t megkapjuk, még a következőket kell észrevennünk. Ha bármely n testőrhöz van olyan (n+1)-edik, aki mind az n-et legyőzte, akkor bármely (n-1) testőrt legalább (n+1) győzött le. Tegyük fel ugyanis, hogy az A1, A2, ..., An-1 testőröket csak a B1, B2, ..., Bn testőrök győzték le. A feltétel szerint létezik olyan C testőr, aki a B1, B2, ..., Bn mindegyikét legyőzte. Ez nem lehet azonos semelyik Ai-vel sem, hiszen Ai-t mindegyik Bj legyőzte. Kell lenni olyan D testőrnek is, aki az A1, A2, ..., An-1, és C testőröket legyőzte (2. ábra). D nem lehet azonos egyetlen Bj-vel sem, mivel D legyőzte C-t, viszont mindegyik Bj kikapott C-től. Másreszt D-nek meg kell egyeznie valamelyik Bj-vel, hiszen A1, A2, ..., An-1 mindegyikét csak a B1, ..., Bn testőrök győzték le. Ellentmondásra jutottunk, ami állításunkat igazolja. Hasonlóan juthatunk ellentmondásra abból a feltevésből, hogy az Ai-ket n-nél kevesebb testőr győzte le.
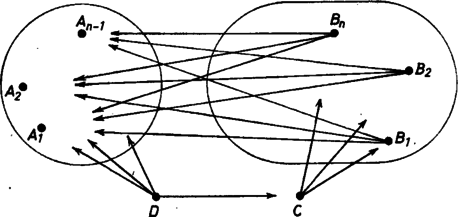Így tehát f(n)≥g(n-1,n+1)2n-1(n+2)-1, ahogyan az (2)-ben szerepel.
Ahhoz, hogy az f(n)≤n2⋅2n+1=k egyenlőtlenséget igazoljuk, semmi mást nem kell tennünk, mint a k testőr közötti k(k-1)/2 küzdelem eredményét úgy megválasztanunk, hogy bármely n testőrt valaki legyőzzön.
Sőt ezeket nem kell konkrétan megadnunk, elegendő bizonyítani, hogy a k(k-1)/2 küzdelem eredménye megválasztható úgy, hogy bármely n testőrt valaki legyőzzön.
A helyzet hasonló ahhoz, amikor azt akarjuk bizonyítani, hogy az a1=1, a2=2, an+1=an+an-1(n≥2) sorozat első 1001 tagja között van kettő olyan, melyek ugyanarra a számjegyre végződnek. Itt is elegendő megkeresnünk ezt a kettőt, de ehelyett igazolhatjuk azt is, hogy ilyen pár mindig kiválasztható anélkül, hogy tudnánk, mik is lesznek a párnak az elemei.
Esetünkben ez a következőképpen fog történni. Megbecsüljük annak a valószínűségét, hogy a lovagi torna végeredménye ,,jó'' lesz. Ha ez a valószínűség pozitív, akkor készen vagyunk, a lehetetlen esemény valószínűsége ugyanis 0.
Tegyük fel tehát, hogy annak valószínűsége, hogy az i-edik testőr legyőzi a j-ediket, i-től és j-től függetlenül 1/2. Tegyük fel továbbá, hogy a küzdelmek kimenetele egymástól független. Legyen p annak a valószínűsége, hogy tetszőleges n testőrhöz található olyan (n+1)-edik, aki mind az n-et legyőzte. Ha most a küzdelmek minden lehetséges kimenetele mellett található n testőr, akiket senki sem győzött le, akkor a fenti esemény a lehetetlen esemény, és így p=0. Így tehát megmutatjuk, hogy p≠0 vagy ami ugyanaz, hogy 1-p<1, akkor a testőrök közötti küzdelmek eredménye megválasztható úgy, hogy bármely n testőrhöz lehessen találni olyan (n+1)-ediket, aki mindegyiküket legyőzte.
Legyenek B1, B2, ..., Bn tetszőleges testőrök. Annak valószínűsége, hogy az A testőr mindegyik Bi-t legyőzi, 1/2n, hiszen mindet 1/2 valószínűséggel győzi le, és a küzdelmek eredménye egymástól független. Így annak valószínűsége, hogy A nem győzi le mindet, 1-1/2n, és így annak valószínűsége, hogy a B1, B2, ..., Bn-től különböző (k-n) testőr egyike sem győzi le B1, B2, ..., Bn mindegyikét,
q=(1-12n)k-n,
hiszen ezek még mindig független események. Így akárhogyan választunk ki n testőrt, q annak a valószínűsége, hogy senki sem győzi le mind az n-et.
A k testőr közül n testőrt(kn)-féleképpen választhatunk ki. Így annak a valószínűsége, hogy van olyan n-es, akit senki sem győz le, legfeljebb (kn)⋅q, azaz
1-p≤(kn)⋅q.
Itt már nem feltétlenül áll fenn egyenlőség, ugyanis az összegzett események már nem zárják ki egymást. Mivel
(kn)≤knésq<(1-12n)k,
az 1-p<1 egyenlőtlenség igazolásához elegendő megmutatni, hogy
kn(1-12n)k<1,
ha k=n2⋅2n+1. Mindkét oldalból n-edik gyököt vonva és k értékét behelyettesítve, a bizonyítandó egyenlőtlenség
n2⋅2n+1[(1-12n)2n]2n<1.(6)
Ennek igazolásához szükségünk lesz a következő két egyenlőtlenségre:
(1-1k)k<e-1ésk2⋅2k+1<e2k.(7)
Az e=limn→∞(1+1n)n=2,71... Az első az ismert (1+1k-1)k>e egyenlőtlenség reciproka, a másodikat k-ra vonatkozó teljes indukcióval könnyen igazolhatjuk.
(7) első egyenlőtlenségét k=2n-re alkalmazva
n2⋅2n+1[(1-12n)2n]2n<n2⋅2n+1⋅e-2n⋅e2n⋅e-2n=1
(7) második egyenlőtlensége szerint. Ezzel (6)-t és ezzel (1) második egyenlőtlenségét is igazoltuk.
Az f(n) függvény értékét tehát két korlát közé sikerült szorítanunk. Az alábbi táblázatban n≤6-ra tüntettük fel a korlátok, illetve f(n) értékét. Az, hogy f(1)=3, triviális, az f(2)=7 egyenlőséget az F. 2159. feladat megoldásában bizonyítottuk. f(3) pontos értékét E. és G. Szekeres számították ki.
 

n  1    2    3    4    5    6  (n+2)2n-1-1  2    7    19    47    111    255f(n)     3    7    19    ?    ?    ?  n2⋅2n+1     4    32    144    512    1600    4608  
 

Megadták 19 testőr közötti 171 küzdelem végeredményét úgy, hogy bármely három testőrhöz legyen egy negyedik, aki mindhármukat legyőzte: az i-edik testőr pontosan akkor győzze le a j-ediket, ha az i+19-j kifejezés 19-cel osztva az 1, 4, 5, 6, 7, 9, 11, 16 vagy 17 maradékot adja. Az olvasóra bízzuk annak ellenőrzését, hogy ez valóban jó.
Az n=4 értéktől fölfelé f(n) értéke nem ismeretes, sőt még azt sem tudjuk, hogy az f(n)n⋅2n sorozat korlátos-e. Megjegyezzük, hogy a konstrukcióból f(4)-re adódó legjobb felső korlát 311 (a legkisebb olyan k, amelyre (k4)q<1 fennáll), ennél jobb felső korlátot nem ismerünk. Sőt, bár tudjuk, hogy 311 testőr közötti küzdelmek eredményét meg lehet választani úgy, hogy bármely négy testőrt valaki legyőzzön, eddig még senki nem adott meg ilyet. Még annak eldöntése is, hogy f(4) egyenlő-e 47-tel, szinte reménytelennek látszik. A 47 testőr közötti 1081 mérkőzésnek 21081≈10300 különböző végeredménye lehet, és ha mindről átlag 0,1 másodperc alatt el tudjuk dönteni, hogy jó-e vagy sem (ami egyenként (474)=178365 vizsgálatot jelent), akkor az utolsó esetre is több mint 10290 év múlva kerülne sor. Csak győzzük kivárni!