Cím: A sárkánygörbe II.
Szerző(k):  Csirmaz László 
Füzet: 1979/március, 97 - 100. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Előző számunk hátsó borítóján egy sárkánygörbét láthattunk. A görbe a következőképpen készült. Kiindultunk az A0A1 szakaszból (1. ábra), ezt A1 körül pozitív irányban 90∘-kal elforgattuk, kaptuk A0A1A2 töröttvonalat. Ezt A2 körül pozitív irányban 90∘-kal elforgattuk, kaptuk az A0A1A2A3 töröttvonalat stb. Végül az így kapott kacskaringós vonalat A0 körül még háromszor 90∘-kal megforgattuk. (Előbb a sarkokat legömbölyítettük: ne legyen a sárkány olyan szúrós.) Két dolgot kellett bizonyítanunk: 1. a görbe sohasem metszi saját magát, 2. a görbe "kitölti'' az egész síkot. Nézzük meg pontosan, mit is jelentenek ezek az állítások.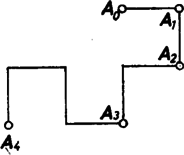

 

 
1. ábra

 

A sárkánygörbét négyzethálós papírra érdemes rajzolnunk. Ha A0A1 éppen egy kis négyzet oldala, akkor a töröttvonal minden oldala egy-egy négyzetoldal lesz. Az, hogy a görbe nem metszi saját magát, azt jelenti, hogy minden négyzetoldalon legfeljebb egyszer halad át (az A0-ból induló másik három ággal együtt), bár egy-egy rácspontba kétszer is befuthat. A síkot a görbe "kitölti'', ha bármely négyzetoldalon legalább egyszer végigmegy, feltéve, hogy görbénkből már elég sokat megrajzoltunk. Ezeket az állításokat fogjuk igazolni.
 

 
2. ábra

 

Először is módosítsuk a sárkánygörbét egy picit: ne egy közönséges szakaszból induljunk bunkó ki, hanem egy "bunkós'' szakaszból, amilyen a 2. ábrán látható. Legyen az előírás szerint elkészített töröttvonal A0A1A2...Ai, ahol Ai a töröttvonal utolsó pontja. Ezt A0 körül még háromszor 90∘-kal elforgatjuk, kapjuk az Si görbét. A 3. ábrán 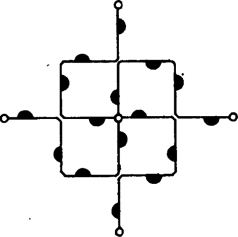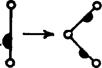S3 látható.
 

 
3. ábra

 

 
4. ábra

 

Elegendő állításainkat ezekre a bunkós sárkánygörbékre igazolni, hiszen a bunkókat lehagyva megkapjuk a közönséges (más néven mezei) sárkánygörbéket. A továbbiakban alapvető fontosságú a következő:
Ha Si-ben minden egyes bunkós szakaszt a 4. ábrán látható két kisebb, egymáshoz derékszögben csatlakozó bunkós szakaszra cserélünk le (az irányítás megtartása mellett!), továbbá a kapott alakzatot 45∘-kal elforgatjuk és 2-szeresére nyújtjuk, éppen Si+1-et kap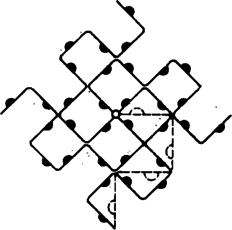juk.
 

 
5. ábra

 

Az 5. ábrán látható, mit kapunk S3-ból a szakaszok lecserélése után, a szaggatott vonal S3 egy ágát mutatja. Az állítás igazsága azonnal következik a sárkánygörbe definíciójából, ennek ellenére azt kérjük az olvasótól, hogy amíg ez nem teljesen világos előtte, ne menjen tovább.
Minden Si görbére igaz a következő három állítás:
(1) a görbe semelyik szakaszon sem halad át kétszer (vagy annál többször);
(2) minden rácspontba a bunkós szakaszok vagy mind a "fejükkel'' (◯- csúcsok) vagy mind a "talpukkal'' (□-csúcsok) futnak be (lásd a 6. ábrát), egy csúcsba természetesen négynél kevesebb szakasz is befuthat;
(3) az ◯-csúcsok és a □-csúcsok a rácspontokon felváltva, sakktáblaszerűen helyezkednek el.
Az (1) állítás mondja ki, hogy a sárkánygörbe sohasem metszi magát, a (2) és (3) állítások ennek bizonyításához szükségesek. Teljes indukciót alkalmazunk: az S1, S2, S3 görbékre (1), (2) és (3) is teljesül. Tegyük fel, hogy Si-re igazak. Mivel (1), (2), (3)-ban nem szerepel sem a görbe mérete, sem elhelyezkedése, elegendő ezeket Si+1 helyett arra az alakzatra igazolnunk, melyet Si-ből a bunkós szakaszok lecserélésével kapunk. Jelöljük ezt 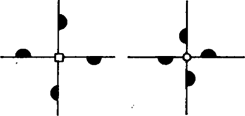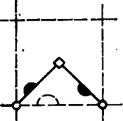Ti-vel.
 

 
6. ábra

 

 
7. ábra

 

A Ti-nek megfelelő rácspontok egyrészt Si rácspontjai, másrészt az alapnégyzetek középpontjai. Lecseréléskor a négyzetek középpontjaiba a kis bunkós szakaszok talpa, a négyzetek csúcsaiba azok feje mutat. Így (2) és (3) Ti-re biztosan teljesül (7. ábra). (1) igazolásához tegyük fel, hogy OA a Ti görbe egy szakasza, ahol O az ABCD alapnégyzet középpontja (8. ábra). Azt kell megmutatnunk, hogy OA-t nem kaphattuk meg kétszer is, két különböző Si-beli szakasz lecserélésekor. Az OA szakaszt csak az AB vagy az AD lecseréléséhez kaphattuk, azaz vagy AB vagy AD Si-hez tartozik (lehet, hogy mindkettő). Különböztessünk meg két esetet: a) A◯-csúcs; b) A□-csúcs. Tudjuk, hogy Si-re igaz (3), ezért a B, C és D csúcsoknak (Si-ben) olyanoknak kell lenniük, mint ahogyan az ábrán jelöltük. S mivel Si-re igaz (2) is, azért az AB-n, illetve AD-n a bunkó (feltéve, hogy AB, ill. AD az Si-hez tartozik) csak a jelölt helyen állhat. Az a) esetben OA-t kizárólag AB, a b) esetben kizárólag AD lecserélésével kaphatjuk meg. Evvel (1)-et is bizonyítottuk.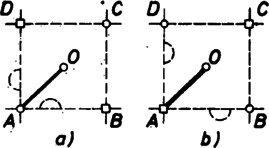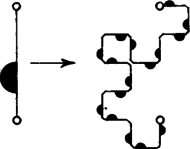
 

 
8. ábra

 

 
9. ábra

 

Összefoglalva: igazoltuk, hogy a sárkánygörbe sohasem metszi saját magát. Hátra van még az, hogy a görbe kitölti a síkot. Ehhez megjegyezzük, hogy ha ugyanabból a szakaszból kiindulva elkészítjük Si-t és Si+1-et, akkor Si része Si+1-nek: ha a sárkánygörbe valamit elfoglalt, azt már soha el nem engedi. Így azt kell bizonyítani, hogy ha A0A1 éppen egy kis négyzet oldala, akkor bármely négyzetoldal valamelyik Si-ben (és akkor az összes későbbiben is) benne lesz. Ezt az előzőhöz hasonlóan tesszük. Figyeljük meg, hogy ha Si-ben minden bunkós szakaszt a 9. ábrán látható vonallal helyettesítünk, majd a kapott alakzatot négyszeresére nyújtjuk, Si+4-et kapjuk. Így például a 10. ábrán S3+4=S7 látható (bunkók nélkül).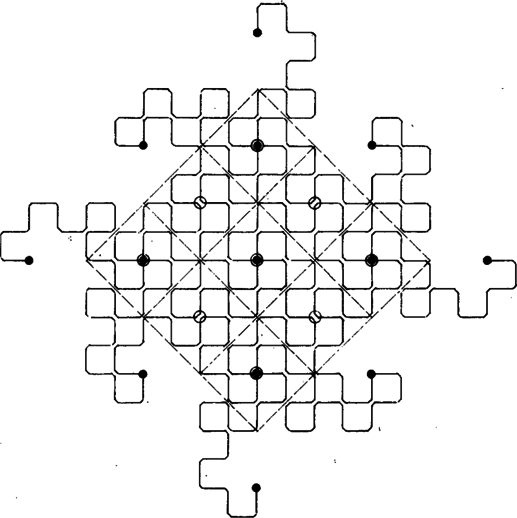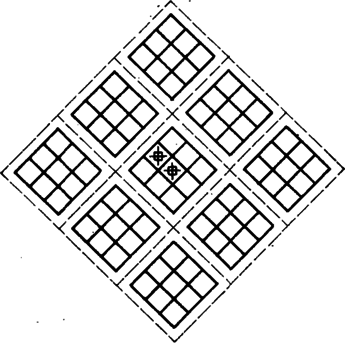
 

 
10. ábra

 

 
11. ábra

 


S7-ben kilenc, S3-mal egybevágó részsárkány is van (szaggatott vonallal elkerítve). Ezek mindegyikéből S7+4=S11-ben egy-egy S7 sárkány lesz, és azokban újból 9-9 S3 részsárkány, összesen 81 (11. ábra). S ha most olyan szerencsénk van, hogy az S7 részsárkányok kilógó "fejei'' éppen kitöltik a köztes részt, azaz ott újabb S3 részsárkányok keletkeznek, akkor készen is vagyunk: S7-ben 3×3 szomszédos S3 van, S11-ben pedig már 11×11. S15-ben ezek mindegyikéből kilenc S3 keletkezik, de a közöttük levő részek is kitöltődnek (ugyanúgy, mint S11 esetében), azaz itt már egy oldalon 3⋅11+10=43 szomszédos S3 található. Általában S4k-1-ben található szomszédos S3 részsárkányok száma (22k-1+13)2, ami például azt is jelenti, hogy az A0 körüli A0A1⋅22k-1+13 sugarú körbe eső minden alapnégyzet oldala az S4k-1 görbéhez tartozik.
A bizonyítás befejezéséhez már csak szerencsénket kell ellenőriznünk. A 12. ábrán négy, sarkosan álló S7 sárkány fejeit rajzoltuk le. Ezek jól láthatóan minden helyet elfoglalnak.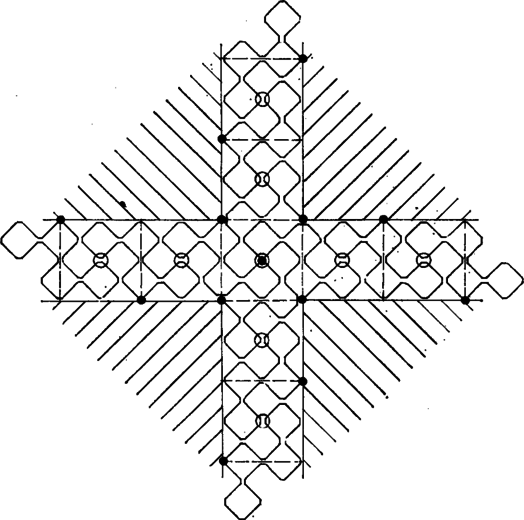
 

 
12. ábra