|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.
A lineáris programozás megalkotása a szovjet Kantorovics [9], továbbá két amerikai: Dantzig [5] és Koopmans [10] nevéhez fűződik. Kantorovics és Koopmans 1975-ben Nobel-díjat, Dantzig pedig 1976-ban az Amerikai Egyesült Államokban állami díjat kapott a lineáris programozás felfedezéséért és az ezzel kapcsolatos további alapvető tudományos eredményekért.
A lineáris programozás jellegét illetően sokféle vélemény alakult ki a keletkezése utáni években, és a vele megismerkedni szándékozók ma is felteszik a kérdést: mi is ez tulajdonképpen? Talán geometria, algebra, kombinatorika, numerikus módszer, függvénytan vagy számítástechnika? Sok jele van annak, hogy kezdetben elsősorban geometriai jellegű tudománynak tartották. Mielőtt Kantorovics [9] könyve 1939-ben megjelent, 1938-ban vitát rendeztek Leningrádban és geométereket kértek fel bírálóknak. Dantzig [6] könyvének 24. oldalán ezt írja: "A konvex poliéder csúcsain való haladás (mely egyébként a szimplex módszer alapja) gondolatát először elvetettük, mert intuitív alapon ineffektívnek látszott. Egy másik geometriában hatékonynak tűnt, ezért szerencsére kipróbáltuk és elfogadtuk''.
A következő szakasz szendvicskészítésről szóló példájában látni fogjuk, hogy ha a feltételeknek megfelelő egyenlőtlenségeket ábrázoljuk a koordinátarendszerben, a sík azon pontjainak összessége, amelyek eleget tesznek a feltételeknek, azaz az ún. megengedett megoldások egy konvex sokszöget alkotnak, és hogy optimális megoldás mindig található e sokszög csúcsai között. E tények valóban azt sejtetik, hogy a geometriának nagy szerep jut a lineáris programozásban.
Később, amikor előtérbe került a lineáris programozási feladat megoldási módszerének végességi kérdése, kitűnt, hogy erre a geometriai jellegű megfontolások már nem alkalmasak és a kombinatorikai jellegű gondolatok kerültek előtérbe. Arról van szó ugyanis, hogy ‐ amint ezt később látni fogjuk ‐ a megoldási módszer során egyik tábláról a másikra megyünk, bizonyos szabályok betartásával, és arra törekszünk, hogy a véges sok lehetséges tábla között egy számunkra alkalmasat találjunk. Ez pedig kombinatorikai jellegű gondolkodásmódot igényel, noha nem támaszkodunk meglevő kombinatorikai eredményekre. Az első végességi bizonyítást Charnes adta 1952-ben [3] cikkében, mely egy évvel később a [4] könyvben is megjelent. Egy további végességi bizonyítást tartalmaz Dantzig, Orden és Wolfe 1955-ben megjelent [7] dolgozata. Az utóbbinak egy elegánsabb változata található Gale 1960-ban megjelent [8] könyvében, továbbá a szerző [11] könyvében és [12] dolgozatában.
E két utóbb említett mű tárgyalásmódja mellőz minden megszorítást és egyben elemi, csak igen egyszerű lineáris algebrai fogásokat alkalmaz. A mostani cikkbe ezt építjük be úgy, hogy semmilyen matematikai előismeretet nem tételezünk fel.
Az angliai lineáris programozási iskola Beale [1] és a magyar származású Vajda [13] munkássága révén kifejlesztett egy "változócentrikus'', függvénytani jellegű tárgyalásmódot. Ennek ma is sok híve van, legutóbb az 1976-ban Budapesten tartott IX. Nemzetközi Matematikai Programozási Szümpozion oktatási szekciójában van de Panne kardoskodott mellette. Ebben a cikkben elfogadjuk ugyan a változócentrikus tárgyalást, ám összeházasítjuk a kombinatorikai tárgyalással.
Minthogy a gyakorlatban előforduló lineáris programozási feladatok általában nagy méretűek, a "hagyományos'' numerikus módszerek nagy szerepet játszanak a tényleges megoldási módszer kialakítása során. Ennek számítógépes programját is meg kell alkotni, érthető tehát, hogy sokan a lineáris programozási feladat megoldását elsősorban a numerikus módszerek közé tartozónak, illetve számítástechnikai jellegűnek tekintik.
A lineáris programozás tehát, mint minden alkalmazott matematikai tudomány, sokarcú. Ám a bevezető jellegű oktatásban le kell egyszerűsíteni a dolgokat. Ennek sikerült megtalálni egy olyan lehetőségét, amely nem nélkülözi a matematikai egzaktságot. Kis méretű feladatokkal dolgozunk, ezért nincs szükségünk a kerekítési hibákra, az információtárolás és a műveletszám minimalizálására figyelő speciális eljárások beépítésére. Megmutatjuk, hogy egy alkalmas szabály betartásával véges sok lépésben el tudunk jutni egy optimális megoldáshoz.
A lineáris programozás feladata
Lineáris egyenlőtlenségekből és lineáris egyenlőségekből álló feltételeknek eleget tevő , , rendezett szám -esek közül ki kell választanunk olyan rendezett szám -est, melyre egy előírt lineáris (első fokú) függvény a lehető legnagyobb, illetve a lehető legkisebb értékét veszi fel. Előfordulhat, hogy feltételeink ellentmondásosak, továbbá az is, hogy van ugyan a feltételeknek eleget tevő rendezett szám -es, ám nincs véges nagyságú szélsőérték. E két esetben a gyakorlati feladatot rosszul fogalmaztuk meg. Ez a tény az esetek nagy részében nem dönthető el ránézéssel, hanem csak a megoldási módszer alkalmazása során tűnik ki. Ezért a feltételek összeférhetőségének és a véges szélsőérték létezésének az eldöntését is a lineáris programozás feladatához soroljuk.
Néhány, lineáris programozásra vezető gyakorlati feladat
A lineáris programozást igen széles körben alkalmazhatjuk. E néhány példa bemutatásával csupán ízelítőt adunk azokból. Az olvasó tetszésére bízzuk, hogy ezek közül melyeket tanulmányozza át. A legelső, szendvicskészítéssel kapcsolatos feladat az egyetlen, amely nem hagyható el, ugyanis ezen illusztráljuk a lineáris programozás grafikus és algoritmikus megoldási módszereit. Az egyes feladatok megoldásait is közöljük; ezeket az olvasó a későbbiekben ismertetendő módszerrel maga is kiszámíthatja. A szénelosztás feladata esetében azonban ezt a módszert nem ajánljuk, erre a speciális feladatra gyorsabb módszer is van, amellyel ebben a cikkben nem foglalkozunk.
Szendvicskészités. Egy társasági összejövetelre szendvicseket készítünk, mégpedig két fajtát. Ezek egy-egy darabja az alábbi összetételű:
Kenyér van otthon bőven, ám a további összetevők mennyisége már korlátozott. Rendelkezésünkre áll:
A célunk az, hogy a lehető legtöbb szendvicset készítsük. Ha , ill. jelöli az egyes szendvicsfajtákból készítendő mennyiséget, akkor feladatunk a következő:
A feladat megoldását grafikusan a következő módon végezhetjük el. Az 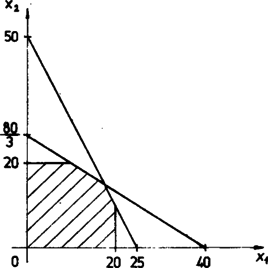ábrán a vonalkázott sokszög jelenti a sík azon pontjainak összességét, amelyek eleget tesznek a feladat feltételeinek. Ezek közül a legnagyobb összeget szolgáltató pontot a következő módon választhatjuk ki: egy egyenlőszárú derékszögű háromszög alakú vonalzót végigcsúsztatunk egy másik vonalzón, mely az tengellyel egybeesik ‐ a ábrának megfelelő módon ‐, majd megállunk akkor, amikor a vonalzó átlójának és a vonalkázott sokszögnek még van közös pontja, de a vonalzó akármilyen kis továbbhaladása esetén ilyen közös pont már nincs.
 1. ábra
 2. ábra
Esetünkben ez az eljárás egyetlen pontot eredményez, mely a
egyenesek metszéspontja. Innen adódik, hogy a legnagyobb összeget akkor kapjuk, amikor és .
Az eredeti gyakorlati feladat megoldását csak közelítőleg kaptuk meg, hiszen nem egész szám, fél szendvicset pedig nem készítünk. Van módszerünk arra is, hogy az , ismeretlenekkel kapcsolatos fenti feltételeken kívül még ezekre az egész értékűség követelményét is előírva, megoldjuk a feladatot. Ezzel a bonyolultabb kérdéssel e helyen nem foglalkozunk. Megjegyezzük, hogy az egész értékűség természetesen nem minden lineáris programozási feladatban jogos követelmény, és még ha jogos is, elhanyagolhatjuk, ha nem tartjuk lényegesnek a meghatározandó darabszámok ily módon adódó csökkenését vagy túllépését.
Ha az eredeti feladattal kapcsolatban az egész értékűséget megkívánjuk, akkor ‐ amint az az előbbi grafikus módszerrel könnyen adódik ‐ három, ugyanazt a maximumot szolgáltató megoldást nyerünk. Ezek a következők:
Optimális termelési terv készítése. Egy teherautókat gyártó vállalat egyéves termelési tervet készít. Meg kell határozni, hogy ötféle autótípus mindegyikéből mennyit gyártsanak egy év folyamán. A gyárnak van két nagyobb üzemegysége: a karosszériaüzem és a motorüzem, továbbá öt kisebb szerelőcsarnoka, mindegyik autótípus számára egy-egy. A karosszéria- és a motorüzem egy időben csak egy-egy autótípushoz gyárt karosszériát, illetve motort, be kell osztani tehát, hogy az egy év időt hogyan használják fel az öt autótípus számára. A szerelőcsarnokok egymás munkáit nem tudják átvállalni.
Ha a karosszériaüzem csak egy autótípushoz gyártana karosszériát, akkor db legyártásához rendre , , , és évre volna szükség.
Ha a motorüzem csak egy autótípushoz gyártana motort, akkor db legyártásához rendre , , , és évre volna szüksége.
Az öt szerelőcsarnok kapacitása évente , , , , ill. autó összeszerelése.
Végül megadjuk, hogy az egyes autótípusok egy-egy darabjának eladása révén a gyár tiszta haszna ezer forintos egységben kifejezve , , , , illetve egység.
Nem törődve azzal, hogy az autók száma csak egész szám lehet, feladatunkat az alábbi módon fogalmazzuk meg:
Az első feltétel a karosszériaüzemmel, a második a motorüzemmel, a többiek az összeszerelő üzemekkel kapcsolatosak. A feladat részletes megoldásával nem foglalkozunk. Eredményként a következő mennyiségeket kapjuk: | |
Svájci családi óragyár. Jakab testvérével, Jánossal és annak fiával, Dániellel családi óragyárat létesít. Négyfajta órát gyárthatnak, ám nem tudják még, hogy melyikből mennyi legyen, mondjuk, egy hét termelése. Az alábbi táblázatban összefoglaltuk, hogy egy-egy óra gyártásához hány munkaórát használnak fel, továbbá mennyi a nyereségük egy-egy órán, végül pedig, hogy heti hány munkaórában termelnek. (Például az fajta óra elkészítéséhez Jakabnak órát, Jánosnak órát és Dánielnek órát kell dolgoznia. A szerk.)
Kérdés, hogy hány darabot gyártsanak az egyes órafajtákból hetenként ahhoz, hogy a haszon a lehető legnagyobb legyen, ha még ismeretes az is, miszerint az első és a második fajtából együtt heti darabnál többet nem tudnak eladni. Jelölje , , , az egyes fajtákból egy hét alatt gyártandó mennyiségeket. A feladat az alábbi módon fogalmazható meg:
A feladat megoldásaként az alábbi számok adódnak: | |
Ezt úgy értelmezhetjük, hogy hét alatt az első fajtából harmincat, a másodikból semmit, a harmadikból hetvenet és a negyedikből száznegyvenet kell gyártaniuk.
Optimális szénelosztás. Négy bányából öt erőműhöz szállítunk szenet. Egy alkalommal, amikor éppen egy elosztási tervet készítünk, az erőművek szénigényei a következők ( tonnás egységben kifejezve):
Egyszerűség kedvéért tegyük fel, hogy a bányákban összesen ugyanannyi szén van, mint az igények összege, éspedig a következő megoszlásban ( tonnás egységben kifejezve):
Feltesszük továbbá; hogy a szén szállítási költsége mindenütt arányos a szállított mennyiséggel. Egy tonna szén szállítási költségeit ‐ valamilyen egységben kifejezve ‐ az alábbi táblázat tartalmazza:
Kérdés, hogy honnan hová mennyi szenet szállítsunk, hogy a szállítási költségek összege a lehető legkisebb legyen?
Ha jelöli az -edik bányából a -adik erőműbe szállítandó mennyiséget (célszerű most kettős indexet használni), akkor a feladat a következő módon fogalmazható meg:
| |
A fenti megoldásban csupán a zérótól különböző mennyiségek megadására szorítkozunk. Ezek a következők:
Menütervezési probléma. Fogyókúrás gyümölcskoktélt állítunk össze úgy, hogy előírjuk négy vitaminfajtából a koktél vitamintartalmának alsó szintjét, továbbá minimalizáljuk a szénhidrát összmennyiségét. A gyümölcsök grammjában levő vitamin- és szénhidrátmennyiségeket, továbbá az említett alsó szinteket az alábbi táblázat tartalmazza:
Jelölje , , az egyes gyümölcsfajtákból felhasználandó mennyiségeket grammos egységekben kifejezve. Feladatunk a következő:
A feladat megoldásaként a következő értékek adódnak:
A lineáris programozási feladat megoldása
A lineáris programozási feladat megoldására mind a mai napig a Dantzig által 1951-ben közölt módszert alkalmazzák leginkább. Ennek egy egyszerű variánsát fogjuk ismertetni.
A feladat feltételeinek eleget tevő , , rendezett szám -eseket megengedett megoldásoknak nevezzük. A továbbiakban feltesszük, hogy feladatunk olyan alakú, hogy csupán az , , feltételekben áll egyenlőtlenség, az egyéb feltételekben pedig egyenlőség, közelebbről: lineáris egyenlőség. A szendvicses feladat numerikus megoldása előtt majd példát mutatunk arra, hogy mi módon lehet a feladatot a most említett, ún. kanonikus (egységesített) alakra hozni, ha az eredetileg nem volt ilyen. Még azt is feltesszük, hogy az egyenlőséges feltételek ún. kifejezett alakúak bizonyos "változókra'' nézve, amin azt értjük, hogy mindegyik egyenlőséges feltételben van olyan változó, mely a többiekben nem szerepel (másképpen kifejezve: a többiekben zéró együtthatóval szerepel). Ilyen pl. az alábbi feltételrendszer:
mely kifejezett az , , változókra nézve. A kifejezett változókat más néven bázisváltozóknak is nevezzük. Még azt is feltesszük, hogy ha a bázisváltozóktól különböző többi változó helyébe zérót helyettesítünk, akkor az egyenlőségekből a bázisváltozók számára automatikusan adódó értékek nemnegatívak. A fenti példában pontosan ez a helyzet, ugyanis és helyébe zérót téve, az , , adódik.
Ha a kanonikus alakú feladat eredetileg nem ilyen, akkor is ilyen alakúra hozható, feltéve, hogy egyáltalán van megengedett megoldás, amint azt a későbbiekben megmutatjuk.
Most egy olyan feladattal foglalkozunk, amelyben maximumot keresünk. A minimum-feladat erre visszavezethető, ha a minimalizálandó kifejezést -gyel megszorozzuk. A maximalizálandó kifejezést célfüggvénynek, a legnagyobb célfüggvényértéket adó megengedett megoldást ‐ ha ilyen egyáltalán van ‐ optimális megoldásnak nevezzük. Általában ha egy halmaz minden eleméhez egyértelműen hozzárendelünk egy számot, akkor ezt a hozzárendelést függvénynek nevezzük. Most a feltételek által meghatározott , , rendezett szám -esek mindegyikéhez rendelünk hozzá egy-egy számot, ily módon alkotjuk meg a célfüggvényt. Pl. az és az alábbi | | (2) |
nemnegativitási feltételeknek eleget tevő , , , , rendezett számötösökön értelmezhetjük az alábbi célfüggvényt: | | (3) |
Az egyenlőségekből az , , változók számára adódó kifejezéseket jobb oldalán a megfelelő helyekre behelyettesítve a célfüggvényre olyan alak adódik, amelyben , , már nem (vagy ha úgy tetszik, zéró együtthatóval) szerepel, mégpedig: Azt a feladatot, amelyben a (4) célfüggvény maximalizálandó az (1) és a (2) feltételek mellett, az alábbi alakban írjuk fel:
A feladatot a konstansok és az együtthatók alábbi táblázatából egyértelműen rekonstruálhatjuk:
1. tábla
A táblában a zérók kiírása vagy elhagyása tetszés szerint történhet. A tábla bal oldalán a kifejezett változókat és a célfüggvény függő változóját írjuk fel, a tábla tetején pedig felsoroljuk valamennyi változót. Most két tételt említünk meg, amelyeket a lineáris programozási feladat megoldásakor használunk fel.
1. tétel. Ha a tábla felső sorában álló számok ‐ az elsőt nem számítva ‐ mind nemnegatívak, akkor a kifejezett változókat a mellettük álló konstansokkal, a többi változót -val egyenlővé téve, a feladat optimális megoldását nyerjük.
A tétel igaz voltát az feladat egy módosítottján szemléltetjük. A módosítás abban áll, hogy az együtthatóját a célfüggvényben megváltoztatjuk, helyett -et írunk a zárójelen belül, miáltal az új célfüggvény a következő lesz: Minthogy , , azonnal adódik, hogy ; és a célfüggvényértéket valóban megkapjuk, ha , továbbá , , .
2. tétel. Ha a tábla felső sorában ‐ az első számot nem számítva ‐ van olyan negatív szám, hogy az alatta álló számok mind nempozitívak, akkor a célfüggvény nem korlátos felülről, azaz akármilyen nagy számnál nagyobb értéket felvesz alkalmas megengedett megoldás esetén.
Ezt a tételt is az feladat egy módosítottján szemléltetjük. A módosítás most abban áll, hogy az első és a második egyenlőséges feltételben a zárójelen belül együtthatóját helyett -ra, illetve helyett -re változtatjuk. Az így nyert feladatban választunk egy tetszőleges , , , , megengedett megoldást; -et növelve, az egyenlőségek érvényben tarthatók az , , bázisváltozók értékeinek alkalmas megválasztásával, miközben a nem bázisváltozók értékét nem változtatjuk (most az tartozik ebbe a kategóriába). Eközben a célfüggvény értéke minden határon túl nő, vagyis tényleg nem korlátos felülről.
A fenti két tételben két különböző típusú tábláról van szó. Van egy harmadik típus is, melyben a felső sorban az első számot kihagyva ‐ van negatív szám és az alatta álló számok között van legalább egy pozitív. Mindegyik tábla a három kategória valamelyikébe tartozik. Az feladathoz tartozó tábla a harmadik csoportba tartozik.
Ekkor eljárásunk a következő: a bázisváltozók valamelyikét megszüntetjük mint bázisváltozót, helyette egy olyan változó, mely eddig nem volt bázisváltozó, azzá válik. Az új bázisváltozó céljára minden olyan változó megfelel, melynek a célfüggvényben a kerek zárójelen belüli együtthatója negatív. Ezek közül tetszőlegesen kiválasztunk egyet bejövő változó gyanánt; ám a kimenő változó meghatározása már nem tetszőleges. Ezt úgy kell megválasztanunk, hogy a célfüggvényben szereplő konstans lehetőleg növekedjék, de legalábbis ne csökkenjen, a feltételek konstansai pedig maradjanak nemnegatívak az új bázisváltozók esetében. Mindkét célt elérjük, ha vesszük azokat az egyenlőséges feltételeket, amelyekben a bejövő változó ‐ zárójelen belüli ‐ együtthatója pozitív, majd meghatározzuk mindegyik ilyen egyenlőségen belül a konstans tag és a bejövő változó együtthatójának a hányadosát és amelyik egyenlőség esetében ez a hányados a legkisebb, annak a bázisváltozója lesz a kimenő változó. Ezek után az előbbi módon kiválasztott egyenlőséges feltételt a bejövő változó együtthatójával végigosztjuk, majd a célfüggvényből és a többi egyenlőséges feltételből ugyanezt a változót kiküszöböljük az új bázisváltozóhoz tartozó egyenlőséges feltétel alkalmas konstansszorosainak hozzáadásával. Megjegyzendő, hogy az új feltételek a régiekkel egyenértékűek, a célfüggvény pedig semmit nem változik értékében, csak alakjában, hiszen csupán zérót adtunk hozzá.
Bár a fentiek alapján nagyjából világos, hogy hogyan nyerjük az új táblát a régiből, a teljesség kedvéért ezt a szabályt röviden összefoglaljuk. Ha az változó bejön a bázisba, pedig kimegy a bázisból, akkor:
az új táblában sorát úgy nyerjük, hogy a régi táblában az -nek megfelelő sort végigosztjuk azzal az elemével, amelyik az oszlopában áll;
az új tábla minden egyéb sorát úgy származtatjuk, hogy a neki megfelelő, régi táblabeli sor oszlopában álló elemével az új tábla -nak megfelelő sorát elemenként végigszorozzuk, majd az így kapott sort elemenként levonjuk a régi táblabeli sorból.
Alkalmazzuk a fent leírt lépést az feladatra. Csak egy negatív szám van a tábla felső sorában az utolsó öt pozícióban, ez -hez tartozik, tehát bejön. Minthogy és a minimumot az első egyenlőséges feltételben kapjuk, ezért a kimenő bázisváltozó. Az új feladatot szükségtelen kiírni, elég az új tábla megadására szorítkozni, ez pedig a következő:
2. tábla
Minthogy a felső sor utolsó öt pozíciójában minden szám nemnegatív, optimális megoldáshoz jutottunk, amely a következő: | |
Ezt a módszert nevezik Dantzig módszerének.
Ha Dantzig módszerének végrehajtása során a tábla bal felső sarkában álló szám állandóan növekszik, akkor soha nem térhet vissza a bázisváltozók egy olyan összessége, mely korábban már szerepelt. A kifejezett változók ugyanis a teljes táblát és így a bal felső sarokban álló elemet is egyértelműen meghatározzák. Minthogy pedig csak véges sok különböző módon lehet a kifejezett változókat kiválasztani, az eljárásnak véges sok lépés után be kell fejeződnie, vagy az , vagy a tételnek megfelelő tábla elérésével. Ha a tételnek megfelelő táblához jutottunk, akkor nyilván rosszul fogalmaztuk meg az eredeti gyakorlati feladatot, ahhoz kell tehát visszatérnünk.
A bejövő változó oszlopának és a kimenő változó sorának kereszteződésében álló elemet szokás sarokelemnek nevezni. Ennek a pozíciónak a megjelölése egyértelműen meghatározza, hogy milyen számítások révén jutunk el az új táblához. Ezért az általános szokásnak megfelelően a sarokelemet mindig bekarikázzuk.
Prékopa András
IRODALOM
[1] E. M. L. Beule: Cicling in the dual Simplex Algorithm, Naval Research Quarterly Logistics, 2/1955/269‐276.
[2] R. G. Bland: New Finite Pivoting Rules for the Simplex Method, Mathematics of Operations Research, 2(1977)103‐107.
[3] A. Charnes: Optimality and Degenaracy in Linear Programming, Econometrica, 20 (1952) 160‐170.
[4] A. Charnes, W. W. Cooper and A. Henderson: An Introduction to Linear Programming, Wiley, New York, 1953.
[5] G. B. Dantzig: Maximization of a Linear Function of Variables Subject to Linear Inequalities, a [10] cikkgyűjteményben 339‐347.
[6] G. B. Dantzig: Linear Programming and Extensions, Princeton University press, Princeton, New Jersey, 1963.
[7] G. B. Dantzig: A. Orden and P. Wolfe: The Generalized Simplex Method for Minimizing a Linear Form under Linear Inequality Restraints, Pacific Journal of Mathematics, 5 (1955) 183‐195.
[8] D. Gale: The Theory of Linear Economic Models, McGraw-Hill, New York, 1960.
[9] L. V. Kantorovics: Matematicseszkije Metodi v Organizacii i Planirovanii Proizvodsztva, L. G. U. 1939.
[10] T. C. Koopmans (szerkesztő): Activity Analysis of Production and Allocation, Wiley, New York, 1951.
[11] Prékopa A.: Lineáris Programozás I., Bolyai János Matematikai Társulat, 1968.
[12] Prékopa A.: A lineáris programozás egy kombinatorikai jellegű tárgyalásáról, Matematikai Lapok, 22 (1971) 7‐24.
[13] S. Vajda: The Theory of Games and Linear Programming, Wiley, New York, 1956.
A Bevezetés további részeit az utolsó bekezdés kivételével az olvasó elhagyhatja, ez nem akadályozza a megértést.Tábla helyett használják a táblázat szót is.A programozási nyelvekben elterjedt szokás szerint a számok felírásában tizedespontot és nem tizedesvesszőt használunk. (A szerk.) |
PDF | MathML