Kezdőlap


Cím:	Labirintusok II.
Szerző(k):	Csirmaz László
Füzet:	1979/január, 1 - 6. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1960-as években a szegedi Kibernetikai Laboratóriumban készítettek egy ,,katicabogarat'', melynek a következő feladata volt. Rátették egy $5 \times 5$ négyzetre osztott asztallap jobb alsó sarkára. Az egyik négyzet közepére egy kis mágnest helyeztek, ezt kellett a katicának megkeresnie úgy, hogy közben egyes osztóvonalak fallal el voltak zárva. Az 1. ábrán a válaszfalak egy lehetőségét vastag vonallal húztuk ki. A katica bekapcsolás után forgolódni kezdett, kereste az utat. Majd elindult egy irányba; ha falba ütközött, visszament a kis négyzet közepére, ott $90^{\circ}$ -kal elfordult és újra elindult. Mikor ráakadt a mágnesre, zümmögni kezdett és pöttyeit villogtatta. Ráadásul menet közben ,,megtanulta'' a mágneshez vezető utat is: ha visszatették a jobb alsó sarokba, már minden próbálkozás nélkül a legrövidebb úton haladt a mágnes felé (az ábrán ezt az utat a szaggatott vonal jelzi).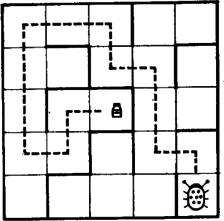

1. ábra

A katica, melynek működését nem ismerjük, valószínűleg a következőképpen működött. (Az egyszerűség kedvéért tekintsünk el attól, hogy a katica ,,tanult'' is.) Ha beérkezett egy mező középpontjába, azonnal balra fordult és elindult. A katica csápjaiban érzékelők voltak, melyek jelezték, ha falba ütközött. Ekkor visszahátrált a mező közepéig, ott jobbra fordult

90^{\circ}

-kal és ismét megindult. Ha itt is fal volt előtte, megint visszahátrált, jobbra fordult és megindult stb.
Rajzoljuk be az 1. ábrába a katica útvonalát! Megtalálná-e a katica akkor is a mágnest, ha azt másik mezőbe tennénk át? És ha a katicát máshonnan indítjuk? El lehet-e helyezni a válaszfalakat úgy, hogy a katica ne jusson el a mágneshez? Tudna-e az olvasó a válaszfalak elhelyezésére olyan elégséges feltételt mondani, ami már biztosítja, hogy a katica megtalálja a mágnest?

A katica problémája egy labirintusbejárási probléma. Ennek megoldására sokféle eljárást találtak ki. Közülük a legegyszerűbb a jobbkéz-szabály; tegyük jobb kezünket a labirintus falára és menet közben mindig érintsük. Ezzel a módszerrel a bejárattól indulva nem feltétlenül jutunk el az útvesztő közepéig, de mindenesetre visszajutunk a bejárathoz, ami sokszor nem megvetendő lehetőség. Természetesen jobb kezünk helyett használhatnánk a balt is, az eredmény nem változik. De ha egyszer elindultunk, végig ugyanazt a kezünket kell használnunk.

Merre haladna a katica a jobbkéz-szabály szerint, és merre a balkéz-szabály szerint? Meg tudnánk-e magyarázni, miért követi a katica a balkéz-szabály szerinti útvonalat?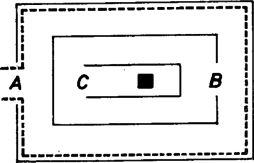

2. ábra

A jobb, illetve balkéz-szabály nem mindig vezet célhoz, például a 2. ábra labirintusán nem érnénk el a középpontot jelképező fekete négyzethez. Ugyanakkor a Hampton Court-beli útvesztő esetén akár a jobbkéz, akár a balkéz-szabály működik, a bejárattól a középpontig és onnan visszajuthatunk, ahogyan azt a 3. ábra mutatja.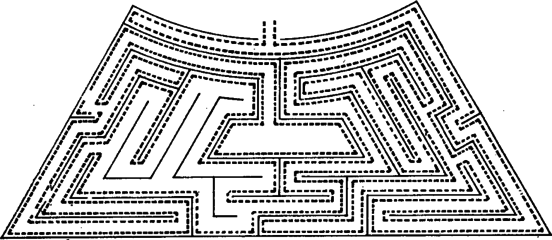

3. ábra

Mielőtt a 2. ábrán látható labirintusra is működő módszert írnánk le, magukat az útvesztőket kell pontosabban definiálni. A labirintusokban vannak utak, és ahol az utak véget érnek, elágaznak vagy találkoznak, termek. Jelöljük a termeket egy-egy ponttal, és két pontot kössünk össze, ha vezet út a megfelelő termek között. Így például az 1. ábrán az asztal mezői a termek, és két szomszédos terem között van út, ha a válaszfal hiányzik. Egy-egy termet a középpontjában levő ponttal jelölve, a 4. ábrán látható hálózatot kapjuk. Hasonlóan a 2. ábrán három útelágazás (terem) van,

A

B

és

C

, ezenkívül a középpontnak és a kijáratnak is megfeleltetünk egy-egy termet, azaz pontot. A hálózatot az 5. ábra mutatja. Végül a 6. ábrán a Hampton Court útvesztőjének hálózata látható. (Ellenőrizzük!) Az ilyen hálózatokat gráfoknak nevezzük, a pontokat csúcsoknak, a köztük futó vonalakat éleknek. Minden labirintushoz hozzárendelhetünk tehát egy gráfot, aminek néhány (de legalább egy) csúcsa jelzi a labirintus kijáratát. Feltesszük ezekről a gráfokról, hogy a ,,kijárat'' csúcsokból egyetlen él indul ki és, hogy a gráf bármely csúcsából bármelyikbe az éleken el tudunk jutni (azaz a gráf összefüggő).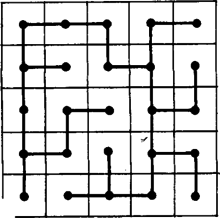

4. ábra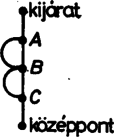

5. ábra

6. ábra

Tegyünk a gráf valamelyik csúcsába egy robotot, melynek feladata lesz a kijárat megkeresése. A robotnak pontosan meg kell mondanunk, hogy mikor mit tegyen, nem szabad utasítás nélkül hagynunk. Ha például olyan helyzetbe kerül, amikor azt csinálhat, amit akar, akkor az utasításunk ez lesz: most pedig csinálj azt, amit akarsz.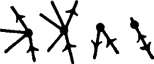

7. ábra

Ahhoz, hogy robotunk a labirintust a jobbkéz-szabály szerint (balkéz-szabály szerint) járja be, például a következő utasításokat kell kiadnunk: ,,Indulj el tetszőleges élen! Ha egy csúcsba beérkeztél és az a csúcs kijárat, állj meg! Ha nem, a csúcsból kiinduló élek közül válaszd ki az első olyat, amelyik jobbra (balra) van, majd a kiválasztott élen menj tovább!'' A 7. ábrán néhány csúcsra felrajzoltuk, hogy a robot a jobbkéz-szabály szerint merre halad.
Próbálja meg az olvasó bizonyítani, hogy ha a ,,jobbkezes'' robot egy gráf tetszőleges csúcsából indulva mindig eljut valamelyik kijárathoz, akkor a gráf szükségképpen fa; továbbá ha a gráf fa, akkor a robot tetszőleges csúcsból indítva - valamelyik kijáratot feltétlenül megtalálja. (A fa gráf fogalmát lásd pl. Kömal 54. kötet 198. o.)
Ezt az állítást kissé átfogalmazva szükséges és elégséges feltételt kapunk arra, hogyan kell a szegedi katica asztalán a válaszfalakat elhelyeznünk ahhoz, hogy a katica biztosan megtalálja a mágnest, bárhonnan indul is. Szükséges marad-e ez a feltétel, ha kikötjük, hogy a katicának a jobb alsó sarokból kell indulnia (de a mágnes bárhol lehet)?

Ott áll tehát robotunk a gráf egyik csúcsában és várja utasításainkat, amelyeknek olyanoknak kell lenniük, hogy mindig elvezessék a robotot egy, ,,kijárat''-csúcsba, függetlenül a gráf felépítésétől és a kezdőponttól. Adjunk a robot egyik kezébe piros festékkel teli vödröt, a másikba zöld festékkel telit. A robot a gráf éleit fogja befesteni: bizonyosakat zöldre és bizonyos, már zöld éleket pirosra. (Természetesen kezdetben a gráf egyik éle sem színezett.) A festés bármely további fázisában lehetnek a gráfnak festetlen élei (ezek a szabad utak), zöld élei (ezeken egyszer áthaladt a robotunk) és piros élei (ezeken kétszer is átment).
A robotnak a színezéshez a következő utasításokat adjuk:
1. Ha ,,kijárat''- csúcsban vagy, akkor állj meg!
2. Ha a csúcsból legfeljebb egy zöld él indul ki és van színezetlen kiinduló él is, akkor válaszd ki ezek egyikét, menj át rajta és fesd át zöldre! (Azaz tovább folytatja az útját.)
3. Ha a csúcsból pontosan egy zöld indul ki és az összes többi piros (azaz zsákutcába jutott), akkor menj vissza a zöld élen és fesd be pirosra!
4. Ha (a 2. utasítás szerint) egy zöld élen jutottál a csúcsba, de onnan (ezzel az éllel együtt) már legalább két zöld él indul ki, akkor menj vissza azon az élen, amelyiken jöttél, és fesd át pirosra!
5. Ha a fenti feltételek egyike sem teljesül, állj meg és adj hibajelzést! (Erre azonban nem kerülhet sor.)
Az így kapott zöld színű élek egymáshoz csatlakoznak, és egy olyan (önmagát nem metsző) utat alkotnak, melynek kezdőpontjából indítottuk a robotot, és melynek végpontjában áll. A piros élek tiltott élek, ezekről útközben már kiderült, hogy nem érdemes rajtuk átmenni. A lépések számára vonatkozó teljes indukcióval lehet igazolni, hogy a zöld színű élek valóban ilyen utat alkotnak. Ezért ha a robot a kezdőponttól különböző csúcsban van, az 1., 2., 3. vagy 4. utasítások valamelyike biztosan alkalmazható. A kezdőpontban is csak akkor vagyunk bajban, ha a belőle kiinduló összes élet a robot már pirosra festette. Az is igazolható, hogy ha a kezdőponttól különböző csúcsból piros él is és színezetlen él is indul, akkor zöld színű is.

8. ábra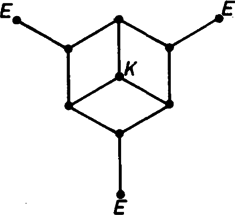

9. ábra

Tegyük fel, hogy az utasítások végrehajtása ellenére a robot nem talál ki a labirintusból, ebből ellentmondásra fogunk jutni.
Az utasítások végrehajtásakor a robot csak a kezdőpontban akadhat el. Mivel a zöld színű élek mindig egy (önmagát nem metsző) utat alkotnak, ez nem indulhat ugyanabból a csúcsból, amelyikben végződik, ebből következik, hogy zöld színű él egyáltalán nem lehet a gráfban. Tudjuk, hogy a gráf bármely csúcsából bármely csúcsába eljuthatunk az élek mentén, így a

K

kezdőcsúcsból az (egyik)

E

,,kijárat''- csúcsba is (8. ábra). Az előző megállapításaink szerint a

K

-ból induló összes él piros, és az

E

-be befutó él nem zöld (hiszen egyáltalán nincs zöld él a gráfban). A befutó él piros sem lehet, mivel piros színű élnek mind a két végpontjában járt a robot. Ezért ez az él színezetlen, következésképp az

E

és

K

közti úton van olyan csúcs, melybe piros él is és színezetlen él is befut. Ekkor a csúcsból, egy korábban elfogadott állítás szerint zöld színű él is indul, ami viszont ellentmond annak, hogy a gráf egyetlen éle sem zöld. Az ellentmondás igazolja állításunkat: a robot biztosan megtalálja a kijáratot, ha pontosan követi az utasításokat.
Megállapíthatjuk, hogy a kijárat keresése közben a robot minden élen legfeljebb kétszer megy végig: először, amikor zöldre festi, és másodszor, amikor pirosra. A labirintusból tehát elég ,,gyorsan'' tud kijutni. S ha a robotot ismét visszatesszük abba a csúcsba, ahonnan indult, már nem kell elölről kezdenie mindent, a zöld éleken végigmenve közvetlenül eljut a kijárathoz. A robot ,,megtanulta'', hogyan juthat ki a labirintusból.
Ennek a módszernek (algoritmusnak) két szépséghibája is van: a robot menet közben össze-vissza festi a labirintust; másrészt nem tudja előre, merre kell majd mennie, ehhez meg kell néznie, hogy a csúcsból, ahol áll, milyen színű élek futnak ki. Van-e olyan módszer, amit követve a robot ,,behunyt szemmel'' is kitalál a labirintusból? Hogy ez mennyire nehéz probléma, talán mutatja az, hogy a robot sohasem tudhatja, hogy egy csúcsban járt-e már korábban vagy most van ott először. És ha nem vagyunk elég gondosak az utasítások kiadásakor, a robot könnyen ,,végtelen ciklusba eshet'', vagyis mindig ugyanazokon az éleken halad körbe-körbe anélkül, hogy ezt észrevenné.
Mint ahogyan az lenni szokott, bonyolult kérdésre bonyolult a válasz is. A megoldás attól függ, milyen segédeszközöket használhat a robot. Ha semmilyet, akkor ilyen módszer nem létezik. Ha megengedjük a robotnak, hogy egy hosszú papírszalagra feljegyzéseket készítsen és a feljegyzések felírását, felhasználási módját nem korlátozzuk, akkor már van módszer.

Ezek pontosabban szólva a következőket jelentik. Minden, segédeszközt nem használó utasításrendszerhez található olyan labirintus-gráf és abban olyan csúcs, hogy a robotot ebből a csúcsból indítva nem talál ki a gráfból. Így például ha az utasítás a jobbkézszabály (vagy a balkéz szabály), akkor a 9. ábrán látható labirintusban a középső

K

csúcsból indulva a robot nem jut el az

E

betűvel jelzett kijáratok egyikéhez sem.
Igazolható az is, hogy ha a robot feljegyzéseket készíthet ugyan, de csak azt a feljegyzését olvashatja el, amelyik a szalagon utolsóként szerepel, s ezt a feljegyzését mindjárt ki is kell radíroznia, már akkor sincs minden labirintusból kitaláló módszer. Ez a megszorítás programozói szakkifejezéssel élve azt jelenti, hogy a robot a memóriáját ‐ a papírszalagot ‐ csak veremnek (stack) használhatja.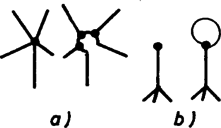

10. ábra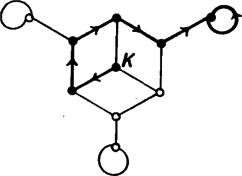

11. ábra

Az egyszerűség kedvéért feltesszük, hogy a labirintus minden csúcsában pontosan három él találkozik. Ez nem jelentős megszorítás: ha több él találkozna, akkor a csúcsot kicsit ,,széthúzva'', ahogyan az a 10. a) ábrán látható, már csupa harmadfokú csúcsot kapnánk. Ha két él találkozik a csúcsban, a csúcsot egyszerűen elhagyjuk, ha pedig egyetlen él fut be, egy hurokélt teszünk rá [10. b) ábra]. Ezzel ugyan a ,,kijárat''- csúcsokba is három él fut be, de ez nem fog zavart okozni.
Robotunk papírszalagjára felír egy természetes számot kettes számrendszerben. Ezután a labirintusban egy kis kirándulást tesz. A kezdőpontból induló három él egyikén elmegy a következő csúcsig és ott jobbra fordul, ha szalagjának végén (az egyes helyiértéken)

1

-es áll, és balra, ha

0

. A következő csúcsnál az utolsó előtti jegy szerint dönti el, hogy merre menjen stb. Végül ha elfogytak a jegyek a szalagján, megáll. Tegyük fel például, hogy a robot szalagján

10011

áll, és a 11. ábra

K

jelű csúcsából indul. A lehetséges három útvonal közül az egyiket megvastagítottuk.
Ha a robot útja során ,,kijárat''-csúcsba érkezik, feladatának vége, a labirintusból kikerült. Ha nem, akkor a szalagon levő jeleket elölről hátrafelé olvasva vissza tud menni a megtett úton a kezdőpontba. Arra kell csak ügyelnie, hogy a visszaúton az

1

-es jelenti a balra kanyarodást és a

0

a jobbra kanyarodást. Ugyanígy oda-vissza megteszi a kezdőpontból induló másik két éllel kezdve is azt az utat, amit a szalagján levő 0 ‐ 1 sorozat mutat. Ha ezekről is visszatér (azaz nem talált kijáratot), a szalagján levő számot eggyel megnöveli, azután újabb kirándulás következik stb.
Az van hátra, hogy megmutassuk: robotunk minden labirintusból kitalál. A kezdőpontból az élek mentén eljuthatunk valamelyik kijárathoz. Hogy a robot éppen ezen az élsorozaton haladjon, az kell, hogy szalagján a

0

-k és

1

-esek abban a sorrendben kövessék egymást, ahogyan azt az élsorozat megköveteli. De természetes számok kettes számrendszerbeli alakjaként minden

1

-gyel kezdődő 0 ‐ 1 sorozat előáll, így a kérdéses 0 ‐ 1 sorozat is előbb-utóbb felkerül a robot szalagjára, legfeljebb egy

1

-es előzi meg. De ez nem baj, mert a robot az éleken haladva már elér a kijárathoz, még mielőtt a felesleges

1

-et le kellene olvasnia.
Mondjuk azt, hogy a robot egyet lép, ha egy élen végigmegy. Ha a gráfban

c

csúcs van, akkor a kezdőponttól a kijáratig vezető út legfeljebb

c

élből állhat, így a robot a kijárat megtalálásáig

6 \cdot 2^{c + 1} = 12 \cdot 2^{c}

lépésnél biztosan kevesebbet tesz meg. Másrészt van olyan

c

csúcsú gráf, amelyben a robotnak legalább

2^{c / 2}

lépést kell tennie a kijárat megtalálásáig. A gráf minden élének két vége van, s minden csúcsból három él indul ki, ezért az élek száma

3 c / 2

. Láttuk, hogy a ,,festékes'' robot minden élen legfeljebb kétszer megy végig, azaz a kijárat megtalálásához legfeljebb

3 c

-t kell lépnie. Az ehhez képest nagyon nagy

12 \cdot 2^{c}

becslés azt mutatja, hogy ,,behunyt szemű'' robotunk programja rossz. Ez nem feltétlenül jelenti azt, hogy ügyetlenek voltunk az utasítások megfogalmazásában. Be lehet bizonyítani, hogy minden ,,behunyt szemű'' robotprogramhoz van olyan

c

csúcsú labirintus s abban olyan kezdőpont, hogy a robot

2^{c / 2}

-nél kevesebb lépéssel nem kerül ki a labirintusból.

A decemberi számban közölt labirintus-
feladat megoldása

A cikk témájához kapcsolódó könyvek

Lovász - Gács: Algoritmusok (Műszaki Könyvkiadó, 1978)

Lukács Ernőné - Tarján Rezsőné: Játékos matematika (Gondolat, 1975)

B. A. Trahtenbrot: Algoritmusok és absztrakt automaták (Műszaki Könyvkiadó, 1978)

Trencsényi Waldapfel Imre: Görög regék (Móra Könyvkiadó, 1973)

Andrásfai Béla: Gráfelmélet (Tankönyvkiadó, 1973)