| Cím: | 1978. A finn-magyar fizikus diáktalálkozó feladatai | ||
| Füzet: | 1978/november, 161 - 165. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Egyéb (KöMaL pontverseny is) | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1. A két acél hengergyűrűt (1. ábra) úgy tolták egymásba, hogy a nagyobb gyűrű hőmérséklete , a kisebbé volt. Ekkor a 2. gyűrű belső sugara -rel nagyobb volt, mint az 1. gyűrű külső sugara. Legalább mekkora tengelyirányú erő szükséges a gyűrűk szétválasztásához, amikor mindkét gyűrű hőmérsékletű, ha a tapadási súrlódási együttható ? (Az acél lineáris hőtágulási együtthatója , Young modulusza .) 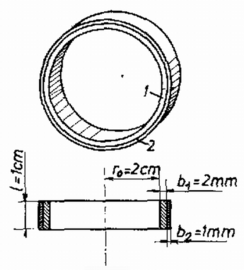 1. ábra Megoldás. Lehűléskor a külső gyűrű összehúzódik. Ha a belső gyűrű nem lenne jelen, belső sugara -rel csökkenne, ami -rel nagyobb a két gyűrű kezdeti távolságánál. Így mindkét gyűrű rugalmas alakváltozást szenved, az gyűrű külső sugara értékkel csökken, a gyűrű belső sugara -vel nő, ahol
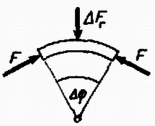 2. ábra
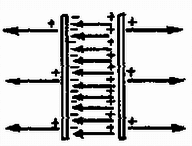
Egy középponti szöghöz tartozó felületen a súrlódási erő maximális értéke 2. A három vezető lemez egyenlő A területű, méretük sokkal nagyobb kölcsönös távolságuknál. Adva van , és ( ábra). a) Kikapcsoljuk a telepet, amikor a lemez az helyen van, azután a lemezt különböző helyzetekbe toljuk. (A lemezhez vezető kapcsolót eközben nem kapcsoljuk be.) Hogyan függ az potenciálkülönbség -től? b) Szétkapcsoljuk az 1. és 3. lemez földvezetékét is, amikor a 2. lemez az helyen van, azután az helyre visszük. Mennyi ekkor az hányados értéke? c) Elvesszük a 3. lemezt. (A 2. lemez helye most is, és továbbra is mindegyik lemez szigetelt állapotban van.) Mennyi most ? d) Mekkora elektrosztatikus erő hat az 1. lemezre a b) és c) esetben? 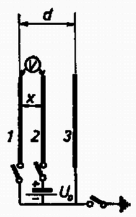 3. ábra Megoldás. a) A kezdeti állapotban két párhuzamosan kapcsolt kondenzátorunk van, mivel a lemez két oldala ekvipotenciális ( ábra). A fegyverzetek területe , távolsága , így a lemez töltése
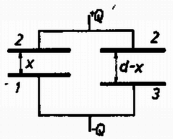 4. ábra A telepet ebben a helyzetben kikapcsoljuk, így a lemez töltése ezután nem változik. változtatásával a két párhuzamosan kapcsolt kondenzátor eredő kapacitását változtatjuk:
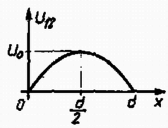 5. ábra b) Amikor a lemez az helyen van, alapján , az lemez töltése
c) A lemezt elvéve olyan kondenzátort kapunk, amelynek két fegyverzetén különböző nagyságú töltés van. Ekkor a feszültséget definíciója alapján, a térerősség meghatározásával számíthatjuk ki. Egy töltéssűrűségű sík lemez térerősségű elektrosztatikus teret hoz létre, így a szuperpozíció elve alapján az és lemez által létrehozott elektromos tér a lemezek között
 6. ábra Az erőt a munkatételből számíthatjuk ki. A b) és a c) esetben az egyes lemezek egymástól és a környezettől szigeteltek, így töltésük állandó. Az és lemez közötti térerősséget az lemez belső felületének felületi töltéssűrűsége határozza meg. A b) esetben Ha az lemezt kicsi távolsággal közelítjük a lemezhez, a térerősség állandó marad, viszont az elektrosztatikus erőtér energiasűrűségének megfelelően az elektrosztatikus energia megváltozását a fegyverzetre ható erő munkája okozza: 3. Párhuzamos fénynyaláb esik egy üveggömbre; a nyaláb egyenlő intenzitású vörös és zöld fény keveréke. (A megfelelő törésmutatók: , .) a) Határozzuk meg a elhajlási szöget az távolság függvényében (l. a 7. ábrát). Ellenőrizzük a 8. ábra grafikonját két számszerű adattal. 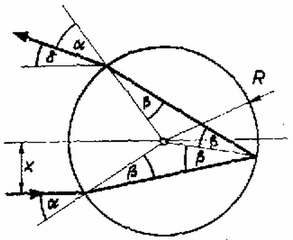 7. ábra 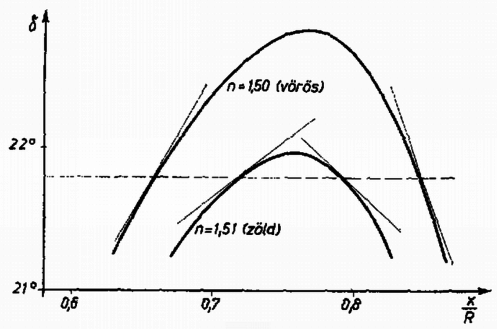 8. ábra 9. ábra d) Növekszik vagy csökken értéke az előzőhöz képest, ha a közvetlenül visszavert sugarak intenzitása nem elhanyagolható? Megoldás. a) A ábra alapján könnyen belátható, hogy A törési törvény alapján b) A grafikon alapján meghatározhatók azon értékei, amelyeknél az eltérülés szöge : A c) A zöld és a vörös fény relatív intenzitását a beeső nyaláb megfelelő keresztmetszeteinek aránya határozza meg: A forgó korong egy d) A gömbről közvetlenül visszaverődő sugarak intenzitása közelítőleg független a fény színétől. Így figyelembevételükkel a kétféle színű fény intenzitás-aránya |