Kezdőlap


Cím:	1978. évi fizika OKTV feladatai
Füzet:	1978/október, 81 - 87. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az I. forduló feladatai

1. Egy elhanyagolható tömegű csigán

0, 4 kg

és

0, 6 kg

tömegű testek lógnak (1. ábra). Nyugalmi állapotból elengedve: a) Mennyi idő múlva találkoznak ?
b) Mekkora ekkor az egymáshoz viszonyított sebességük ?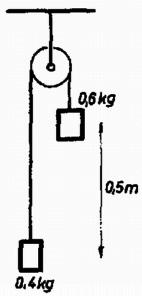

1. ábra

Megoldás. A gyorsulás

\begin{matrix} a = \frac{0, 6 kg - 0, 4 kg}{0, 6 kg + 0, 4 kg} \cdot g = \frac{g}{5} . \end{matrix}

s = 0, 25 m

út megtételéhez szükséges idő:

\begin{matrix} t = \sqrt[]{\frac{2 s}{a}} = 0, 505 s . \end{matrix}

A sebesség ekkor

\begin{matrix} v = \sqrt[]{2 a s} = \sqrt[]{g / 10} = 0, 99 m/s, \end{matrix}

az egymáshoz viszonyított sebesség ennek a kétszerese:

1, 98 m/s

2. Egy háromszögalapú hasáb két téglatestre támaszkodik (2. ábra). A hasáb alaplapjának élei

5 cm

5 cm

és

6 cm

hosszúak. A hasáb oldallapjának felezővonalán támaszkodik a

3 cm

magas téglatestekre. A három test tömege egyenlő. A súrlódás elhanyagolható. Nyugalmi helyzetből elindulva mekkora sebességgel érkezik a hasáb az asztallaphoz ?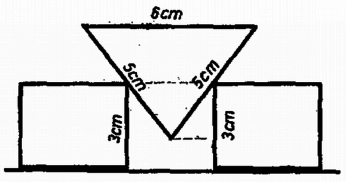

2. ábra

Megoldás. A geometriai viszonyokból következik, hogy a hasáb félmagasságnyi,

2 cm

-es lesüllyedése esetében a téglatestek vízszintesen

1, 5 cm

-rel tolódnak el; ugyanilyen arányban állnak a sebességek és a gyorsulások:

\begin{matrix} 4 : 3 = s_{1} : s_{2} = v_{1} : v_{2} = a_{1} : a_{2} . \end{matrix}

Az 1-es index a hasábra, a 2-es az egyik téglatestre vonatkozik. Az energia-megmaradás törvénye szerint a hasáb lesüllyedésekor végzett munka a három test mozgási energiáját eredményezi:

\begin{matrix} m g h = \frac{m v_{1}^{2}}{2} + \frac{m v_{2}^{2}}{2} + \frac{m v_{2}^{2}}{2} = \frac{m v_{1}^{2}}{2} + m \cdot {(\frac{3}{4} v_{1})}^{2} . \end{matrix}

A megtett út

h = 1 cm = 0, 01 m

, így a hasáb sebessége:

\begin{matrix} v_{1} = 4 \sqrt[]{\frac{g h}{17}} = 0, 304 m/s . \end{matrix}

3. Egy

5 méter

sugarú,

300 kg

tömegű korong szélén

80 kg

tömegű ember áll. A korong az emberrel együtt függőleges tengelye körül kezdetben

0, 1 s^{- 1}

fordulatszámmal forog. A korong szélén álló ember bemegy a korong középpontjába. Mennyi a rendszer energiájának megváltozása ?

Megoldás. Ilyen esetben a szögsebesség és tehetetlenségi nyomaték szorzata, az úgynevezett impulzusnyomaték állandó marad. A tehetetlenségi nyomaték az első állapotban:

\begin{matrix} 0, 5 \cdot 300 kg \cdot {(5 m)}^{2} + 80 kg \cdot {(5 m)}^{2} = 5750 kg \cdot m^{2}, \end{matrix}

a végállapotban

\begin{matrix} 0, 5 \cdot 300 kg \cdot {(5 m)}^{2} = 3750 kg \cdot m^{2} . \end{matrix}

A szögsebesség az első állapotban

2 π \cdot 0, 1 s^{- 1} = 0, 628 s^{- 1}

, ekkor az impulzus-nyomaték

\begin{matrix} 0, 628 s^{- 1} \cdot 5750 kg \cdot m^{2} = 3611 kg \cdot m^{2} / s . \end{matrix}

A második állapotban jelöljük a szögsebességet

ω

-val. Az impulzusnyomaték állandósága folytán:

\begin{matrix} 3750 kg \cdot m^{2} \cdot ω = 3611 kg \cdot m^{2} / s . \end{matrix}

Az új szögsebesség innen

ω = 0, 963 s^{- 1}

, a fordulatszám ennek megfelelően

0, 153 s^{- 1}

. A mozgási energia az első állapotban

\begin{matrix} 0, 5 \cdot 5750 kg \cdot m^{2} {(0, 628 s^{- 1})}^{2} = 1134 joule, \end{matrix}

a második állapotban pedig

\begin{matrix} 0, 5 \cdot 3750 kg \cdot m^{2} \cdot {(0,963 s^{- 1})}^{2} = 1739 joule . \end{matrix}

A mozgási energia növekedése

605 joule

. Egy ilyen mozgás során a mozgási energia nem marad állandó, hanem megnövekszik, a mechanikai energiamegmaradás törvénye nem érvényes. Az ember csak izmaival végzett munka árán képes bejutni a középpontba, ezt pedig szervezete anyagainak kémiai energiájából meríti. Ha az összes energiafajt figyelembe vesszük, akkor a rendszer összenergiája természetesen nem változik.

4. Egy függőleges tengelyhez vízszintes rúd csatlakozik (3a. ábra). A rúdon két egyforma rugóval összekötött, egyenként

1 - 1 kg

tömegű test súrlódás nélkül csúszhat. A rugók nyújtatlan hossza

L = 0, 1 méter

és rugóállandója

D = 10 N/m

. Mekkora állandó szögsebességgel kell a tengelyt forgatni, hogy a külső tömeg

3 L

távolságban legyen a tengelytől ?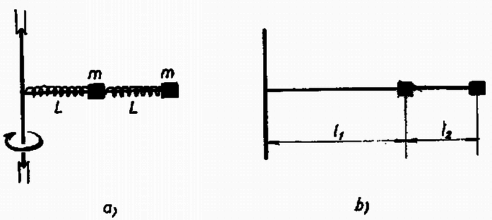

3. ábra

Megoldás. Jelöljük a megnövekedett rugóhosszúságokat

l_{1}

-gyel és

l_{2}

-vel (3b. ábra). A külső tömeget a külső rugó rugalmas ereje kényszeríti a körpályára, ezért

\begin{matrix} D (l_{2} - L) = m ω^{2} \cdot 3 L . \end{matrix}

A belső tömeget a két rugóerő eredője tartja a körpályán:

\begin{matrix} D (l_{1} - L) - D (l_{2} - L) = m ω^{2} l_{1} . \end{matrix}

Az egyenletek összeadásával kiküszöböljük

l_{2}

-t:

\begin{matrix} D (l_{1} - L) = 3 m ω^{2} L + m ω^{2} l_{1}, \end{matrix}

és ebből az első rugóhossz:

\begin{matrix} l_{1} = L \cdot \frac{D + 3 m ω^{2}}{D - m ω^{2}} . \end{matrix}

l_{1} + l_{2} = 3 L

alapján a második rugóhossz:

\begin{matrix} l_{2} = L \cdot \frac{2 D - 6 m ω^{2}}{D - m ω^{2}} . \end{matrix}

ω

meghatározásához legelső egyenletünkbe behelyettesítjük

l_{2}

most kapott értékét; rendezés után kapjuk:

\begin{matrix} 3 m^{2} ω^{4} - 8 D m ω^{2} + D^{2} = 0. \end{matrix}

Ennek megoldása:

\begin{matrix} ω = \sqrt[]{\frac{D}{3 m} (4 \pm \sqrt[]{13}),} ω_{1} = 5, 04 s^{- 1}, ω_{2} = 1, 15 s^{- 1} . \end{matrix}

Eszerint

ω

független

L

nagyságától. A két gyök közül fizikailag csupán

ω_{2}

reális, ugyanis

D < m ω^{2}

, ezért

ω_{1}

esetében

l_{1}

-re negatív érték adódik. Tehát

ω =

= 1, 15 s^{- 1}

. Ennek felhasználásával a megnyúlt rugóhosszak:

\begin{matrix} l_{1} = (- 2 + \sqrt[]{13}) L = 1, 61 L, \\ l_{2} = (5 - \sqrt[]{13}) L = 1, 39 L . \end{matrix}

A II. forduló feladatai

1. Egy

15 méter

magas teremben

10 méter

hosszú fonálon

m_{2} = 0, 96 kg

tömegű test lóg (4. ábra). Ezt az ingát úgy hozzuk mozgásba, hogy az ingatestnek ‐ a lengés síkjában fekvő ‐ vízszintes irányú

v_{1} = 15 m/s

sebességgel

m_{1} = 0, 04 kg

tömegű golyócskát lövünk neki. Ezt mindannyiszor megismételjük, valahányszor az inga balról jobbra függőleges helyzetén halad át. Az ütközés tökéletesen rugalmas. Az inga minden teljes lengése alatt energiájának

k = 5 %

-át veszti el.

(g = 10 {m/s}^{2} .)

a) Mekkora az a legnagyobb magasság, ameddig az inga a leírt módon felvihető ?
b) Hol van a padlón az a sáv, amelybe a visszaeső golyók hullanak ?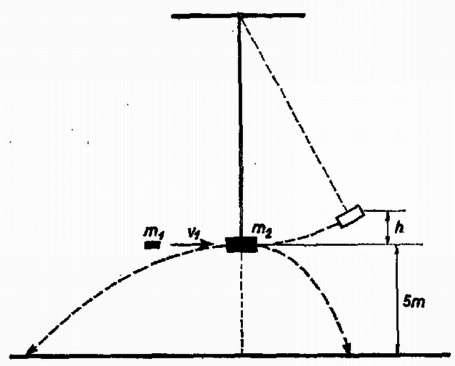

4. ábra

Megoldás. A testek ütközés utáni sebessége legyen

u_{1}

, illetve

u_{2}

. A rugalmas ütközésekre vonatkozó ismert összefüggésekből

\begin{matrix} u_{2} = \frac{(m_{2} - m_{1}) v_{2} + 2 m_{2} v_{1}}{m_{1} + m_{2}} . \end{matrix}

(1)

A végállapotban mint határesetben az inga

u_{2_{\infty}}

-nel repül el jobbfelé, és energiaveszteség után balról a függőleges helyzetbe

v_{2}

sebességgel érkezik, így

\begin{matrix} (1 - k) \cdot \frac{m_{2} u_{2 \infty}^{2}}{2} = \frac{m_{2} v_{2 \infty}^{2}}{2}, \end{matrix}

vagyis

v_{2 \infty} = u_{2 \infty} \sqrt[]{1 - k} .

Másrészt (1) szerint

\begin{matrix} u_{2 \infty} = \frac{(m_{2} - m_{1}) u_{2 \infty} + 2 m_{1} v_{1}}{m_{1} + m_{2}} . \end{matrix}

v_{2 \infty}

előbbi értékét beírva

\begin{matrix} u_{2 \infty} = \frac{(m_{2} - m_{1}) u_{2 \infty} \sqrt[]{1 - k} + 2 m_{1} v_{1}}{m_{1} + m_{2}} . \end{matrix}

Ennek rendezésével kapjuk a végállapotbeli ütközéskor az

u_{2 \infty}

eltávozási sebességet:

\begin{matrix} u_{2 \infty} = \frac{2 m_{1} v_{1}}{m_{1} + m_{2} - (m_{1} - m_{2}) \sqrt[]{1 - k}} = 11, 62 m/s . \end{matrix}

Mivel egynegyed lengés alatt

k / 4

törtrész az energiaveszteség, azért a

h_{\infty}

emelkedési magasságra felírhatjuk, hogy

\begin{matrix} m_{2} g h_{\infty} = \frac{m_{2} u_{2 \infty}^{2} [1 - (k / 4)]}{2}, \end{matrix}

tehát

\begin{matrix} h_{\infty} = \frac{u_{2 \infty}^{2} (1 - k / 4)}{2 g} = 6, 66 m . \end{matrix}

A visszapattanó golyók sebessége:

\begin{matrix} u_{1_{k}} = \frac{m_{1} - m_{2}}{m_{1} + m_{2}} v_{1} = - 13,8 m/s, \\ u_{1} = \frac{(m_{1} - m_{2}) v_{1} + 2 m_{2} u_{2 \infty} \sqrt[]{1 - k}}{m_{1} + m_{2}} = 7, 94 m/s . \end{matrix}

Mivel a golyók

5

méteres magasságból esnek le, esésük

1

másodpercig tart és a földön

- 13, 8

métertől

+ 7, 94

méterig terjedő, összesen

21, 74

méter széles sávon hullanak le.

2. Asztallap szélére

L

hosszúságú pálcát állítunk, amelynek alsó vége súrlódásmentesen egy pecekhez támaszkodik (5. ábra). A pálca lebillen. Milyen magas az asztal, ha a pálca felső végével lefelé függőleges helyzetben érkezik a padlóhoz ?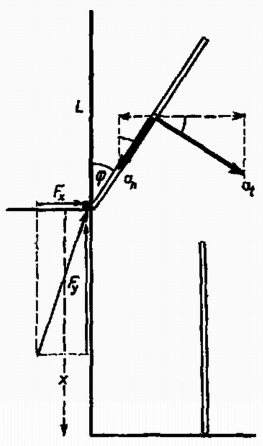

5. ábra

Megoldás. Határozzuk meg a pálcának azt a helyzetét (a

φ

szöget), ahol elválik a pecektől.
A pálca mozgását először úgy vizsgáljuk, mintha alsó vége tengely körül forogna. A tömegközéppont gyorsulásának érintőmenti és tengely felé mutató összetevője:

\begin{matrix} a_{t} = β \cdot \frac{L}{2}, \\ a_{n} = ω^{2} \cdot \frac{L}{2} . \end{matrix}

β

szöggyorsulást a forgás törvényéből kapjuk, mint a forgatónyomaték és a

Θ = m L^{2} / 3

tehetetlenségi nyomaték hányadosát:

\begin{matrix} β = \frac{m g (L / 2) sin φ}{Θ}, β = 3 g \end{matrix}

ω^{2}

az energiamegmaradás törvényéből adódik:

\begin{matrix} m g \cdot \frac{L}{2} (1 - cos φ) = ω^{2} Θ / 2, ω^{2} = \frac{3 g}{L} (1 - cos φ) . \end{matrix}

Felhasználva

β

-t és

ω^{2}

-et, megkapjuk a pálca gyorsulásának összetevőit mint

φ

függvényét:

\begin{matrix} a_{t} = \frac{3}{4} \cdot sin φ, \\ a_{n} = \frac{3}{2} \cdot g (1 - cos φ) . \end{matrix}

E kettő eredője az a gyorsulás, amellyel a tömegközéppont a

φ

-vel meghatározott helyzetben mozog. Ez a gyorsulás természetesen csak akkor jön létre, ha megfelelő erő hat a rúdra. A pálcára a súlyerő és a pecek által kifejtett

F

erő hat. E kettő hozza létre az

a_{t}

és

a_{n}

által meghatározott gyorsulást.
Vizsgáljuk a pecek által a pálcára kifejtett

F

erő vízszintes összetevőjét. Ez hozza létre

a_{t}

és

a_{n}

vízszintes összetevőinek algebrai összegét:

\begin{matrix} F_{x} = m a_{t} cos φ - m a_{n} sin φ = \frac{3}{4} \cdot m g (3 cos φ - 2) sin φ . \end{matrix}

Mivel a pecek csak nyomni képes, azért a pálca akkor válik el az asztal szélétől, amikor

F_{x}

nulla lesz. A

φ = 0

triviális esettől eltekintve az elválás akkor következik be, amikor

cos φ = 2 / 3, φ = 48^{\circ} 11' = 0, 8411

.
Érdemes megvizsgálni a pecek által kifejtett erő

y

irányú összetevőjét,

F_{y}

-t. Ennek nagysága

\begin{matrix} F_{y} = m g - \frac{3}{4} \cdot m g sin^{2} φ - \frac{3}{2} \cdot m g (1 - cos φ) cos φ = \frac{m g}{4} (1 - 6 cos φ + 9 cos^{2} φ) . \end{matrix}

F_{y} = 0

egyenlet megoldása mutatja, hogy

F_{y}

akkor lenne nulla, amikor

cos φ = 1 / 3, φ = 70^{\circ} 27'

, de addigra a pálca már elhagyta az asztal szélét.
A pálca elválásának pillanatában

cos φ = 2 / 3, sin φ = \sqrt[]{5} / 3, tg φ = \sqrt[]{5} / 2

. A tömegközéppont sebességének összetevői

v_{x} = \sqrt[]{g L} / 3, v_{y} = \sqrt[]{5 g L} / 6

, sebessége

v = \sqrt[]{g L} / 2

. Ekkor a középpont

ω = v : (L / 2) = \sqrt[]{g / L}

szögsebességgel forog és ezt az állandó szögsebességét továbbra is megtartja. A leérkezésig még

π - 0, 8411 = 2, 3005

(radiánban kifejezett) szöget kell fordulnia, amihez

t = 2, 3005 / ω = 2, 3005 \sqrt[]{L / g}

idő szükséges.
A tömegközéppont ferde hajítás pályáján mozog. Függőlegesen

x - (L / 2) + (L cos φ) / 2 = x - (L / 6)

utat kell megtennie. A lefelé történő hajítás úttörvénye szerint

\begin{matrix} x - \frac{L}{6} = v_{y} t - \frac{g}{2} \cdot t^{2} = \frac{\sqrt[]{5 g L}}{6} \cdot 2, 3005 \sqrt[]{\frac{L}{g}} + \frac{g}{2} \cdot 2, 3005^{2} \cdot \frac{L}{g} . \end{matrix}

Innen az asztal keresett magassága:

\begin{matrix} x = [\frac{1}{6} + \frac{2, 3005 \sqrt[]{5}}{6} + \frac{2, 3005^{2}}{2}] L = 3, 67 L . \end{matrix}

Az eredmény

g

-től független.

3. Egy

44, 8 liter

térfogatú henger közepén súrlódás mentes dugattyú alul is, felül is

4 gramm 0^{\circ} C

hőmérsékletű héliumot választ el (6. ábra). A henger fala és a dugattyú tökéletes hőszigetelő. Az alsó részben

242 ohm

ellenállású,

220 voltos

, melegítésre szolgáló huzal van. Mennyi ideig kell ezt bekapcsolnunk, hogy a felső részben a hélium hőmérséklete

136, 5^{\circ} C

-ra emelkedjék ? A hélium fajhői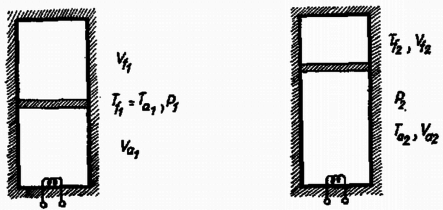

c_{p} = 1, 25 cal / gK = 5, 23 J/gK

és

c_{v} = 0, 75 cal/gK = 3, 14 J/gK

6. ábra

Megoldás. Kifelé nincs munkavégzés, ezért az elektromos munka a gázok belső energiájának növekedésével egyenlő. Így az alsó gáz véghőmérsékletére van szükségünk.
A kezdeti adatok :

V_{f 1} = V_{a 1} = 22, 4

liter,

T_{f 1} = T_{a 1} = 273 K, p_{1} = 1

atmoszféra. A kísérlet végén

T_{f 2} = 409, 5 K;