Kezdőlap


Cím:	1977. évi Eötvös Loránd Fizikaverseny
Füzet:	1978/február, 81 - 84. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat $1977.$ október $29$ -én rendezte $54.$ versenyét Budapesten és $10$ vidéki városban az $1977$ -ben érettségizettek és a középiskolai tanulók részére. A versenyzők $5$ órai munkaidő alatt oldhattak meg három feladatot. Bármely segédeszköz használata megengedett volt. A versenyen $358$ tanuló vett részt. Ismertetjük a feladatokat és megoldásukat.

1. Adva van egy alakjára nézve szimmetrikus lejtő pár (

1

. ábra), a közepe nagyon lapos. A bal fele gumi, igen nagy csúszó súrlódási együtthatóval, jobb fele fém és ennek súrlódási együtthatója elhanyagolható. Egy gumihengert elengedünk a lejtő tetejéről, egyszer balról, egyszer jobbról. Melyik esetben emelkedik a henger a túlsó oldalon magasabbra?
Károlyházy Frigyes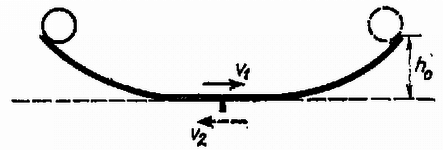

1. ábra

Megoldás. Indítsuk el a hengert a bal oldalról

h_{0}

magasságból. Kezdeti helyzeti energiája

m g h_{0}

. Leérkezve középre, a henger középpontjának sebessége

v_{1}

; a henger mozgási energiája egyenlő a kezdeti helyzeti energiával:

\begin{matrix} m g h_{0} = \frac{m v_{1}^{2}}{2} + \frac{ω^{2} Θ}{2} = \frac{m v_{1}^{2}}{2} (1 + \frac{Θ}{m r^{2}}); \end{matrix}

m

a henger tömegét,

Θ

a tehetetlenségi nyomatékát jelöli. Felhasználtuk, hogy a sima gördülés esetében

v_{1} = ω r

, ahol

r

a henger sugara és

ω

a szögsebessége a középre érkezéskor. A jobb oldalon felfelé haladva a henger súrlódás hiányában megtartja szögsebességét és csak az

m v^{2} / 2

haladási mozgási energiáját képes a

h_{1}

magasságig való felemelkedéskor helyzeti energiává változtatni:

\begin{matrix} m g h_{1} = \frac{m v_{1}^{2}}{2} = \frac{m g h_{0}}{1 + Θ / (m r^{2})} . \end{matrix}

Innen a jobb oldali felemelkedési magasság:

\begin{matrix} h_{1} = h_{0} \cdot \frac{1}{1 + Θ / (m r^{2})} . \end{matrix}

(Ezt a magasságot elérve a henger még pörög

ω

szögsebességgel.)
A hengert jobbról

h_{0}

magasságból elengedve pörgés nélkül ér le középre, ahol középpontjának sebessége:

\begin{matrix} v_{2} = \sqrt[]{2 g h_{0}} . \end{matrix}

A bal oldalon felfelé haladva a henger forgásba jön. Azonban a pörgés nélküli állapotból nem képes pillanatszerűen sima gördülésbe átmenni, egy darabig szükségképpen köszörül. A középpont egyenletesen lassuló mozgást végez,

μ

súrlódási együttható esetében sebessége

t

idővel a köszörülés kezdete után

v_{2} - μ g t

. A köszörülés befejeződik, ha

v_{2} - μ g t = ω r

. Viszont

ω

mint az idő függvénye a forgó mozgás alaptörvénye szerint (a

β

szöggyorsulás a forgatónyomaték és a tehetetlenségi nyomaték hányadosa):

\begin{matrix} ω = β t = \frac{μ m g r}{Θ} \cdot t . \end{matrix}

v_{2} - μ g t = r ω

egyenletből megkapjuk a köszörülés idejét:

\begin{matrix} t = \frac{\sqrt[]{2 g h_{0}}}{μ g} \cdot \frac{Θ / (m r^{2})}{1 + Θ / (m r^{2})} . \end{matrix}

A szögsebesség a köszörülés végén:

\begin{matrix} ω = \sqrt[]{2 g h_{0}} \cdot \frac{m r}{Θ + m r^{2}}, \end{matrix}

a sebesség pedig

\begin{matrix} v = ω r = \frac{\sqrt[]{2 g h_{0}}}{1 + Θ / (m r^{2})} . \end{matrix}

A köszörülés végére megmaradt mozgási energia:

\begin{matrix} \frac{m v^{2}}{2} + \frac{ω^{2} Θ}{2} = \frac{m v^{2}}{2} (1 + \frac{Θ}{m r^{2}}) = \frac{m g h_{0}}{1 + Θ / (m r^{2})} . \end{matrix}

Így a

h_{2}

bal oldali emelkedésre

\begin{matrix} \frac{m g h_{0}}{1 + Θ / (m r^{2})} = m g h_{2}, \end{matrix}

amiből

\begin{matrix} h_{2} = h_{0} \cdot \frac{1}{1 + Θ / (m r^{2})} . \end{matrix}

Ez ugyanakkora, mint az első felemelkedési magasság. Tehát a henger mindkét oldalon ugyanolyan magasra fut fel, függetlenül a súrlódási együttható értékétől. A megoldás során feltételeztük, hogy a köszörülés a pálya vízszintes szakaszán zajlik le.
Figyelembe véve, hogy guruló hengerről van szó,

Θ / (m r^{2}) = 1 / 2

, így az emelkedés magassága

2 h_{0} / 3

. Kiszámíthatjuk a köszörülés útját is, ez

\begin{matrix} s = \frac{h_{0}}{μ} \cdot \frac{[2 + Θ / (m r^{2})] Θ / (m r^{2})}{{[1 + Θ / (m r^{2})]}^{2}} . \end{matrix}

A köszörülés útja henger esetében

5 h_{0} / 9 μ .

2. Az

F

fényforrás egy kisméretű higanygőzlámpa, amely

0, 57 μ m

hullámhosszú sárga és

0, 54 μ m

hullámhosszú zöld fényt bocsát ki (a többit kiszűrtük). A lencse a fényforrást egy messze levő ernyő

P

helyén képezi le (

2.

ábra). A lencse felét egy vékony,

1, 5

törésmutatójú planparalel lemezzel fedjük le. Milyen vastag legyen ez a lemez, hogy a fényfolt

P

-ben minél fényesebb és tisztán sárga színű legyen?
Vermes Miklós

Megoldás. Mindegyik hullámhosszú fény a lemezben fáziskülönbségre tesz szert a levegőben haladóhoz képest. A lemezvastagságot úgy kell megválasztani, hogy ez a fáziskülönbség a zöld fény számára

90^{\circ}

páratlan, a sárga számára páros többszöröse legyen.
A sárga fény hullámhossza levegőben

λ_{10} = 0, 57 μ m

, a lemezben

λ_{1} = λ_{10} / n = 0, 38 μ m

. A zöld fény hullámhossza levegőben

λ_{20} = 0, 54 μ m

, a lemezben

λ_{2} = λ_{20} / n = 0, 36 μ m

(

n

a törésmutató).
A

h

vastagságú rétegben a sárga fényből a lemezben

n h / λ_{10}

, a levegőben

h / λ_{10}

hullám fér el, ezek különbsége: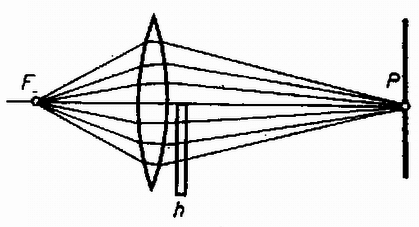

\begin{matrix} \frac{h (n - 1)}{λ_{10}} = k_{1}; \end{matrix}

mivel a sárga fényre erősítést kell kapnunk, ez a

k_{1}

egész szám.

2. ábra

A zöld fényből a lemezben

n h / λ_{20}

, a levegőben

h / λ_{20}

fér el, ezek különbsége a kioltás feltétele miatt

k_{2} + 1 / 2

(

k_{2}

egész szám):

\begin{matrix} \frac{h (n - 1)}{λ_{20}} = k_{2} + \frac{1}{2} . \end{matrix}

A két egyenletet egymással elosztva:

\begin{matrix} \frac{λ_{10}}{λ_{20}} = \frac{19}{18} = \frac{k_{2} + \frac{1}{2}}{k_{1}}, \end{matrix}

rendezve:

\begin{matrix} 19 k_{1} = 18 k_{2} + 9. \end{matrix}

Feltételünknek egész számokból álló

k_{1}

k_{2}

számpárok felelnek meg. Ezek:

k_{1} = 9

k_{2} = 9

;

k_{1} = 27

k_{2} = 28

;

k_{1} = 45

k_{2} = 47

stb. A számpárokhoz tartozó lemezvastagság a

\begin{matrix} h = \frac{λ_{10} k_{1}}{n - 1} \end{matrix}

összefüggésből rendre

10, 26 μ m

;

30, 78 μ m

;

51, 3 μ m

stb.

3. Adva van a térben két kicsiny gömb, ellentétes, abszolút értékben egyenlő töltésekkel. Két félből összerakható, vékony, elektromosan semleges, fémből készült gömbhéjjal az ábrán látható módon körülvesszük az egyik töltést (

3.

ábra).
a) Rajzoljuk meg lehetőleg hűen az erővonal-ábrát!
b) Megváltozott-e a két kicsiny gömb közötti potenciálkülönbség?
Károlyházy Frigyes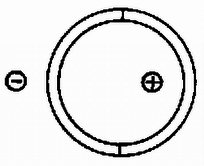

3. ábra

Megoldás. A gömbhéjban létrejövő megosztott töltések közül a pozitívak a negatív golyócska, a negatívok a pozitív golyócska közelében a gömbhéj felszínén helyezkednek el (

4.

ábra). A golyócskák töltéséből az erővonalak ezek felé mennek, természetesen a fém felületét merőlegesen találják el.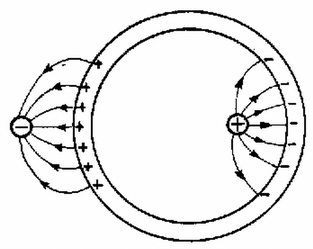

4. ábra

A potenciálkülönbség az egységnyi töltés átvivési munkáját jelenti. Gömbhéj nélkül az átvivés útja

A

(

5.

ábra). Gömbhéj jelenlétében az út először

a

, azután (mivel a fémen nincs potenciálkülönbség) munkavégzés nélkül juthatunk el a gömbhéj túlsó oldalára és ott újra

a

út megtevésével a pozitív golyócskához. Az utak tehát sokkal kisebbek, a térerősség azonban nagyobb.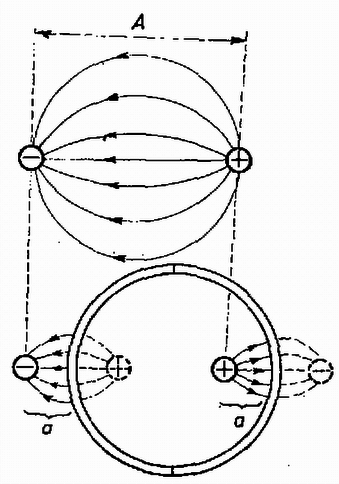

5. ábra

Amikor még nincs ott a gömbhéj, és a negatív töltésű,

ϱ

sugarú golyócska felszínéről visszük át a töltésegységet a

ϱ

sugarú, pozitív töltésű golyócska felszínére, akkor a potenciálkülönbség:

\begin{matrix} U = 2 k Q [\frac{1}{ϱ} - \frac{1}{A - ϱ}] = \frac{2 k Q}{ϱ} \cdot \frac{A - 2 ϱ}{A - ϱ} . \end{matrix}

Ezután behelyezzük a gömbhéjat. Ha a gömb elég nagy, első közelítésben a golyócskák közelében felszínét síknak vehetjük. Ekkor az erővonalak úgy mennek a gömbhéj fala felé, mintha mögötte

a

távolságban

+ Q

töltés volna. Hasonló a helyzet a túlsó oldalon (tükörtöltések). Most a töltésegység átvivési munkája:

\begin{matrix} U = 2 k Q [- \frac{1}{a} + \frac{1}{2 a - a} + \frac{1}{ϱ} - \frac{1}{2 a - ϱ}] = \frac{2 k Q}{ϱ} \cdot \frac{2 a - 2 ϱ}{2 a - ϱ} . \end{matrix}

Ez a potenciálkülönbség mindaddig kisebb a gömbhéj nélkülinél, amíg

a

kisebb, mint

A / 2

. Rajzunk ilyen esetet tüntet fel, tehát a gömbhéj behelyezése csökkenti az eredeti potenciálkülönbséget. Ha figyelembe vesszük, hogy a gömbhéj fala kissé görbült, a hosszadalmas számítás hasonló eredményt ad.

A verseny eredménye

I. díjat nyert Neumer Attila (Bp., Fazekas Mihály Gyak. Gimn., IV. o. t., tanára Szalay Béla és Tóth László). II. díjat nyertek Kriza György (Bp., Fazekas Mihály Gyak. Gimn., IV. o. t., tanára Szalay Béla és Tóth László) és Vankó Péter honvéd (Budapesten a Móricz Zsigmond Gimnáziumban érettségizett Sikó Attiláné tanítványaként). III. díjat nyertek Biegl Csaba honvéd (Budapesten a József Attila Gimnáziumban érettségizett Bakányi Márton tanítványaként) és Magyar Zoltán honvéd (Budapesten a Jedlik Ányos Gimnáziumban érettségizett Galántai Zsuzsa tanítványaként). Dicséretet kaptak jutalommal: Bene Gyula (Miskolc, Földes Ferenc Gimnázium. III. o. t., tanára Zsudel László) és Kovács Zsolt honvéd (Szolnokon a Verseghy Ferenc Gimnáziumban érettségizett Sebestyén István tanítványaként).