Cím: Néhány szó a hálókról
Szerző(k):  Ruttkay Zsófia 
Füzet: 1978/december, 201 - 204. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A Gy. 1799. gyakorlatban (lásd ezen számunk 220. oldalán) legnagyobb közös osztóról, legkisebb közös többszörösről van szó. Két szám legnagyobb közös osztója, illetve legkisebb közös többszöröse lehet a két szám egyike, de lehet egy harmadik szám is. Például 12 és 4 legnagyobb közös osztója, amit (12,4)-gyel szokás jelölni, 4; legkisebb közös többszörösük, aminek jele [12,4], éppen 12. Hasonlóan (12,12)=12; (12,9)=3; (12,5)=1; [12,6]=12; [12,12]=12; [12,8]=24. (Ha a két szám egyenlő, a legnagyobb közös osztójuk és legkisebb közös többszörösük természetesen ugyanannyi.) Akármelyik eset fordul is elő a fentiek közül, két szám legnagyobb közös osztójának, illetve legkisebb közös többszörösének megkeresését tekinthetjük olyan műveletnek, amely két számhoz egy harmadik számot rendel hozzá.
A matematikában gyakran fordulnak elő olyan műveletek, amelyek egy halmaz elemeiből képzett párokhoz a halmaz egy-egy elemét rendelik. Az ilyen műveleteket kétváltozós műveleteknek nevezzük. (Vannak nem kétváltozós műveletek is. Például az, amelyik minden számhoz az ellentettjét rendeli, egyváltozós.)
Néhány példa kétváltozós műveletekre:

a halmaz:a művelet:1.  a természetes számoka legnagyobb  közös  osztó képzése2.  a természetes számoka legkisebb  közös  többszörös képzése3.  a valós számokaz összeadás4.  a valós számoka kivonás5.  a racionális számok,kivéve  a0-t  az osztás6.  a0és1elemekből álló  halmaza szorzás7.  a[0,x]szakaszok halmaza,Mahol  x≧0a halmazelméleti metszet művelet8.  a[0,x]  szakaszok halmaza,  Mahol  x≧0a halmazelméleti unió művelet.

Gyakran fordul elő, hogy ugyanazon a halmazon nem egy, hanem két kétváltozós műveletet is definiálunk. A fenti példák közül az 1‐2., 3‐4., 7‐8. ilyenek. A továbbiakban, ‐ hogy általában is beszélhessünk ezekről ‐ a halmazt H-val, elemeit az x, y, z stb. betűkkel, végül a két kétváltozós műveletet ^, illetve ∨ jelekkel jelöljük. A ^, ∨ műveleteket rendszerint metszetnek,illetve uniónak mondják, de ezek a műveletek (általában) különböznek a szokásos halmazok között értelmezett metszet (∩) és unió (∪) műveletektől. Persze nagyon sokféleképpen lehet a H halmazt kijelölni és azon két kétváltozós műveletet megadni. A továbbiakban csak azokat az eseteket vizsgáljuk, amelyekben a ^, ∨ műveletek eleget tesznek a következő kikötéseknek:
Iax^x=x,Ibx∨x=xIIax^y=y^xIIbx∨y=y∨xIIIax^(y^z)=(x^y)^zIIIbx∨(y∨z)=(x∨y)∨zIVax^(y∨x)=xIVbx∨(y^x)=x

Ha egy H halmazon a ^, ∨ műveletek olyanok, hogy kielégítik a felsorolt nyolc kikötést ‐ matematikai nyelven szólva axiómát ‐, akkor a H halmazt a rajta értelmezett ^, ∨ műveletekkel hálónak nevezzük, és ezt így írjuk: (H,^,∨) háló.
Mit jelentenek valójában a formulákkal leírt hálóaxiómák? Az Ia és Ib azt mondja ki, hogy a halmaz két azonos eleméhez mindkét művelet magát az elemet rendeli. A IIa és IIb,illetve IIIa ésIIIb axiómák ‐ a valós számok összeadásánál és szorzásánál már megismert ‐ kommutatív, illetve asszociatív tulajdonság teljesülését követelik meg. Legérdekesebbek és a hálókra "legjellemzőbbek'' a IVa, IVb axiómák. Ezek a ^, ∨ műveletek egymáshoz való viszonyára vonatkoznak, azt mondják ki, hogy a hálóban a ^, ∨ műveletek között milyen összefüggésnek kell lennie.
Nézzük meg, hogy kiindulási példánkban, az (N, (n), [n])-ban ‐ ahol N a természetes számok halmazát, (n) és [n] a legnagyobb közös osztó képzés,illetve a legkisebb közös többszörös képzés műveletét jelöli ‐, teljesülnek-e a háló-axiómák? Jelöljük a természetes számokat m,n,k,... betűkkel.
Az Ia, Ib axiómák nyilván teljesülnek, mert

(m,m)=m     és  [m,m]=m.  
 

A IIa, IIb axiómák is teljesülnek, mert két szám legnagyobb közös osztója és legkisebb közös többszöröse nem függ a számok sorrendjétől, azaz:

(m,n)=(n,m)   és  [m,n]=[n,m].  
 

A IIIa, IIIb axiómák is fennállnak hiszen már az I. osztályban bizonyítottuk, hogy

(m,(n,k))=((m,n),k)  és  [m,[n,k]]=[[m,n],k].  
 

A IVa, IVb axiómák teljesülését is könnyen beláthatjuk annak alapján, hogy két szám legnagyobb közös osztója nem nagyobb, mint a két szám bármelyike, és két szám legkisebb közös többszöröse nem kisebb, mint a két szám bármelyike.
Tehát a hálóaxiómák teljesülnek, máris láttunk egy "élő'' hálót. Ebben a hálóban ‐ az 1799. gyakorlat szerint ‐ még az alábbi két összefüggés is igaz:

(m,[n,k])=[(m,n),(m,k)]   és  [m,(n,k)]=([m,n],[m,k]).  
 

Ezek az összefüggések a hálók általános nyelvén így írhatók:
Vax^(y∨z)=(x^y)∨(x^z)Vbx∨(y^z)=(x∨y)^(x∨z)

Az Va, Vb összefüggések a két hálóműveletnek ‐ a valós számok szorzásánál és összeadásánál ugyancsak ismert ‐ disztributív tulajdonságát mondják ki. Az olyan hálókat, amelyekben az Va, Vb tulajdonságok is teljesülnek, disztributív hálóknak hívják.
Lássunk további példákat hálókra!
1. Legyen H az egészek halmaza és legyen a k, l egészekre
k∨l=max(k,l),illetvek^l=min(k,l).

2. Álljon H az "igaz'' és "hamis'' elemekből, ^ és ∨ legyenek a logikában szereplő "és'', illetve "vagy'' műveletek, azaz az alábbi művelettáblák írják le a ^, illetve ∨ műveleteket:
^   igaz  hamisigazigaz  hamis  hamis      hamis      hamis  ∨   igaz  hamisigazigaz  igaz  hamis       igaz       hamis  

3. Legyen M egy halmaz, álljon H az M összes részhalmazaiból, az üres halmazt is beleértve. Ekkor H-nak A, B elemeire (melyek M-nek részhalmazai) legyen A^B=A∩B és A∨B=A∪B. Az így kapott hálót M részhalmazhálójának szokás nevezni.
4. Legyen H a [0,1] intervallumon értelmezett valós függvények halmaza. Tetszőleges H-beli f1 és f2 elemekre (függvényekre) legyen f1^f2 az a h, amelyre h(x)=min(f1(x),f2(x)), ha 0≦x≦1, illetve f1∨f2 az a g, amelyre g(x)=max(f1(x),f2(x)), ha 0≦x≦1.
Az olvasó maga könnyen ellenőrizheti, hogy a felsorolt példák valóban hálók.
 

Tovább vizsgálva kiindulási példánkat, (N, (n), [n] )-t, észrevehetjük, hogy az 1 speciális tulajdonságú szám: bármely természetes számnak és 1-nek a legnagyobb közös osztója 1, azaz: (n,1)=1, amit a hálók nyelvén felírva:

VIax  ^  o= o.  
 

Általában, ha egy hálóban van olyan o elem, hogy tetszőleges x H-beli elemre VIa fennáll, akkor a hálót nullelemesnek hívják. Ha van ilyen o, azt (vagy azokat) a háló nullelemének mondják. Tehát (N, (n), [n] ) nullelemes háló, nulleleme az 1.
Lehet-e egy hálóban több különböző nullelem? Tegyük fel, hogy o1 és o2 nullelemek. Ekkor o1-re és o1-re teljesül VIa, azaz
o2^o1=o1éso1^o2=o2.
De IIa miatt o2^o1=o1^o2, így o1=o2, vagyis a két nullelem azonos. Tehát egy hálóban legfeljebb egy nullelem lehet.
Az eddigi axiómák és tulajdonságok olyan párokat alkottak, hogy egy-egy pár 2 tagja hasonló tulajdonságot mondott ki a ^ ,illetve ∨ műveletre. Ennek alapján felírhatjuk a VIa tulajdonság "párját'':

VIbx∨e=e.  
 

Ha egy hálóban van olyan e elem, hogy tetszőleges x H-beli elemre VIb fennáll, akkor a hálót egységelemesnek hívják. Ha van ilyen e, azt (vagy azokat) a háló egységelemének mondják. Könnyen látható, hogy a (N, (n), [n] ) hálóban nincs egységelem. ‐ Ahogyan azt beláttuk, hogy egy hálóban legfeljebb egy nullelem van, ugyanúgy belátható, hogy egységelem is legfeljebb egy lehet.
A (H,^,∨) háló véges, ha H véges sok elemből áll. Ha (H,^,∨) egy véges háló, akkor van benne egységelem és nullelem is. Álljon ugyanis H az x1,...,xn elemekből. Ekkor az Ia, IIa, IIIa, illetve Ib, IIb, IIIb axiómák felhasználásával belátható, hogy
(...((x1^x2)^x3)^...)^xnnullelem,
(...((x1∨x2)∨x3)∨...)∨xnegységelem.
Egy háló végessége tehát elégséges, de nem szükséges feltétel arra, hogy a hálóban legyen egységelem és nullelem.
Az itt felsorolt tulajdonságok mellett még nagyon sok minden mondható a hálókról. Mindenki maga is felfedezhet vagy gyárthat további hálókat, és azokat vizsgálva újabb tulajdonságokat bizonyíthat be. A hálókról további ismeretek és feladatok találhatók Dr. Szász Gábor: Hálóelmélet c. szakköri füzetében (Tankönyvkiadó, 1978).
Gyakorlásul szolgálhatnak a következő feladatok (megoldásuk a szerkesztőségbe küldhető, a legjobb megoldásokat jutalmazzuk):
1. A fenti 1‐4. példák közül melyek a) disztributív, b) egységelemes, c) nullelemes, hálók?
2. Hogyan lehetne az (N, (n), [n]) hálót további elem (elemek) hozzávételével egységelemessé tenni?
3. Adjuk meg az összes, legfeljebb 4 elemű hálót.
4. Bizonyítsuk be, hogy ha e egységelem, o nullelem, akkor tetszőleges x elemre: x^e=x, valamint x∨o=x.
5. Az ábra egy hivatal felépítését szemlélteti: a pontok embereket jelölnek, a pontokat összekötő vonalak az emberek közötti "főnök‐beosztott'' viszonyt. Ha egy 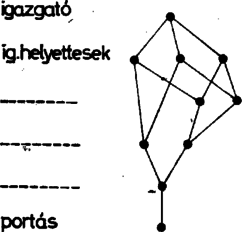X pontból mindig lefelé haladó törött vonalon el lehet jutni az Y ponthoz, akkor Y az X-nek beosztottja és X az Y-nak főnöke.
 
 

Látjuk, hogy ennek a hivatalnak két tetszőleges dolgozója nem mindig van főnök‐beosztott viszonyban, ilyenkor magasabb rangúnak mondjuk azt, akinek a pontja följebb levő sorban van. (Természetesen a főnök is magasabb rangú, mint a beosztottja.) A felrajzolt hivatal olyan, hogy bármely 2 ember közül vagy egyik beosztottja a másiknak, vagy pedig van legalább egy közös főnökük és legalább egy közös beosztottjuk, és közös főnökeik közt van pontosan egy legalacsonyabb rangú, illetve közös beosztottjaik közt van pontosan egy legmagasabb rangú. A közös főnökök közül a legalacsonyabb rangúnak a megkeresése kétváltozós művelet, úgyszintén a közös beosztottak közül a legmagasabb rangúnak a megkeresése is. (Ezekben a műveletekben egy embert önmaga főnökének tekintünk, egyben önmaga beosztottjának is.)
Mutassuk meg, hogy ezzel a két művelettel a hivatal felépítése hálót alkot, továbbá keressük meg az egységelemet és a nullelemet. Rajzoljuk fel különböző típusú hivatalok diagramját!
6. Az 5. feladat ábrájának mintájára rajzoljuk fel az M={1,2,3} halmaz részhalmazhálójának diagramját !